
Thirring model
Encyclopedia
The Thirring model is an exactly solvable quantum field theory which describes the self-interactions of a Dirac field in two dimension.
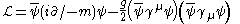
where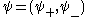 is the field, g is the coupling constant
is the field, g is the coupling constant
, m is the mass
, and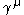 , for
, for 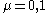 , are the two-dimensional gamma matrices.
, are the two-dimensional gamma matrices.
This is the unique model of two-dimensional, Dirac fermions with a local (self-)interaction. Indeed, since there are only 4 independent fields, because of Pauli
principle, all the quartic, local interactions are equivalent; and all higher power, local interactions vanish. (Interactions containing derivatives, such as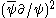 , are not considered because non-renormalizable.)
, are not considered because non-renormalizable.)
The correlation functions of the Thirring model (massive or massless) verify the Osterwalder-Schrader axioms, and hence the theory makes sense as a quantum field theory
.
 -points field correlation is known.
-points field correlation is known.
, many authors tried to solve the massless case, with confusing outcomes. The correct formula for the two and four point correlation was finally found by K. Johnson ; then C. Hagen and B. Klaiber extended the explicit solution to any multipoint correlation function of the fields.
. Though, an explicit formula for the correlations is not known.
J. I. Cirac, P. Maraner and J. K. Pachos applied massive Thirring model for description of optical lattices in .
. This helps to calculate exactly mass spectrum
and scattering matrix. Calculation of the scattering matrix reproduce the results published earlier by Alexander Zamolodchikov
. The paper with exact solution of Massive Thirring model by Bethe Ansatz was first published in Russian. The paper was then translated into English. Ultraviolet renormalization
was done in the frame of Bethe ansatz. The fractional charge appears in the model during renormalization as a repulsion beyond cutoff.
Multi particle production cancels on mass shell.
Exact solution shows once again the equivalence of Thirring model and quantum sine-Gordon model. The Thirring model is S-dual
to the sine-Gordon model. The fundamental fermions of the Thirring model correspond to the soliton
s of the sine-Gordon model.
.
Definition
The Thirring model is given by the Lagrangian density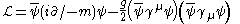
where
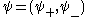 is the field, g is the coupling constant
is the field, g is the coupling constantCoupling constant
In physics, a coupling constant, usually denoted g, is a number that determines the strength of an interaction. Usually the Lagrangian or the Hamiltonian of a system can be separated into a kinetic part and an interaction part...
, m is the mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
, and
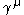 , for
, for 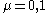 , are the two-dimensional gamma matrices.
, are the two-dimensional gamma matrices.This is the unique model of two-dimensional, Dirac fermions with a local (self-)interaction. Indeed, since there are only 4 independent fields, because of Pauli
Pauli
Pauli is a surname and also a Finnish male given name and may refer to:* Arthur Pauli, an Austrian ski jumper* Gabriele Pauli, a German politician* Hans Pauli, a Swedish monk and alleged sorcerer...
principle, all the quartic, local interactions are equivalent; and all higher power, local interactions vanish. (Interactions containing derivatives, such as
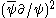 , are not considered because non-renormalizable.)
, are not considered because non-renormalizable.)The correlation functions of the Thirring model (massive or massless) verify the Osterwalder-Schrader axioms, and hence the theory makes sense as a quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
.
Massless Case
The massless Thirring model is exactly solvable in the sense that a formula for the -points field correlation is known.
-points field correlation is known.Exact Solution
After it was introduced by Walter ThirringWalter Thirring
Walter Thirring is an Austrian physicist after whom the Thirring model in quantum field theory is named. He is son of the physicist Hans Thirring, co-discoverer of the Lense-Thirring frame dragging effect in general relativity....
, many authors tried to solve the massless case, with confusing outcomes. The correct formula for the two and four point correlation was finally found by K. Johnson ; then C. Hagen and B. Klaiber extended the explicit solution to any multipoint correlation function of the fields.
Massive Case
The mass spectrum of the model and the scattering matrix was explicitly evaluated by Bethe AnsatzBethe ansatz
In physics, the Bethe ansatz is a method for finding the exact solutions of certain one-dimensional quantum many-body models. It was invented by Hans Bethe in 1931 to find the exact eigenvalues and eigenvectors of the one-dimensional antiferromagnetic Heisenberg model Hamiltonian...
. Though, an explicit formula for the correlations is not known.
J. I. Cirac, P. Maraner and J. K. Pachos applied massive Thirring model for description of optical lattices in .
Exact Solution
In one space and one time dimension the model can be solved by Bethe AnsatzBethe ansatz
In physics, the Bethe ansatz is a method for finding the exact solutions of certain one-dimensional quantum many-body models. It was invented by Hans Bethe in 1931 to find the exact eigenvalues and eigenvectors of the one-dimensional antiferromagnetic Heisenberg model Hamiltonian...
. This helps to calculate exactly mass spectrum
and scattering matrix. Calculation of the scattering matrix reproduce the results published earlier by Alexander Zamolodchikov
Alexander Zamolodchikov
Alexander Borissowitsch Zamolodchikov is a Russian physicist, known for his contributions to condensed matter physics and string theory.Born near Dubna,...
. The paper with exact solution of Massive Thirring model by Bethe Ansatz was first published in Russian. The paper was then translated into English. Ultraviolet renormalization
Renormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
was done in the frame of Bethe ansatz. The fractional charge appears in the model during renormalization as a repulsion beyond cutoff.
Multi particle production cancels on mass shell.
Exact solution shows once again the equivalence of Thirring model and quantum sine-Gordon model. The Thirring model is S-dual
S-duality
In theoretical physics, S-duality is an equivalence of two quantum field theories or string theories. An S-duality transformation maps states and vacua with coupling constant g in one theory to states and vacua with coupling constant 1/g in the dual theory...
to the sine-Gordon model. The fundamental fermions of the Thirring model correspond to the soliton
Soliton
In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
s of the sine-Gordon model.
Bosonization
S. Coleman discovered an equivalence between the Thirring and the sine-Gordon models. Despite the fact that the latter is a pure boson model, massless Thirring fermions are equivalent to free bosons; besides massive fermions are equivalent to the sine-Gordon bosons. This phenomenon is more general in two dimensions and is called bosonizationBosonization
In theoretical physics, one often studies two-dimensional conformal field theory. It has many very special properties. One of them is the equivalence of fermionic elementary fields and bosonic elementary fields. Bosonization also appears in 2D theories which aren't conformal field theories.The...
.

