Composition of relations
Encyclopedia
In mathematics
, the composition of binary relation
s is a concept of forming a new relation from two given relations R and S, having as its most well-known special case the composition of functions.
and 
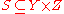are two binary relations, then
their composition
is the relation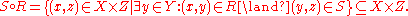
In other words,
is defined by the rule that says 
if and only if there is an element 
such that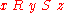 
(i.e. 
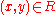and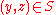 
).
In particular fields, authors might denote by what is defined here to be .
The convention chosen here is such that function composition
(with the usual notation) is obtained as a special case, when R and S are functional relations. Some authors prefer to write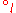
and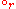 
explicitly when necessary, depending whether the left or the right relation is the first one applied.
A further variation encountered in computer science is the Z notation
:
is used to denote the traditional (right) composition, but ⨾ (a fat semicolon with Unicode code point U+2A3E) denotes left composition. This use of semicolon coincides with the notation for function composition used (mostly by computer scientists) in Category theory
. Because U+2A3E is hard to distinguish from a normal semicolon in some fonts at small sizes, its "capital" version ⨟ (U+2A1F) may be preferable in some fonts. In non-Unicode LaTeX
, the symbol may obtain using the
The binary relations
are sometimes regarded as the morphisms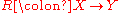 
in a category
Rel
which has the sets as objects. In Rel, composition of morphisms is exactly composition of relations as defined above. The category Set
of sets is a subcategory of Rel that has the same objects but fewer morphisms. A generalization of this is found in the theory of allegories
.
The inverse relation
of is
. This property makes the set of all binary relations on a set a semigroup with involution
.
The compose of (partial) function
s (i.e. functional relations) is again a (partial) function.
If R and S are injective, then is injective, which conversely implies only the injectivity of R.
If R and S are surjective, then is surjective, which conversely implies only the surjectivity of S.
The set of binary relations on a set X (i.e. relations from X to X) together with (left or right) relation composition forms a monoid
with zero, where the identity map on X is the neutral element, and the empty set is the zero element
.
. The usual composition of two binary relations as defined here can be obtained by taking their join, leading to a ternary relation, followed by a projection that removes the middle component.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the composition of binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
s is a concept of forming a new relation from two given relations R and S, having as its most well-known special case the composition of functions.
Definition
If and 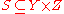are two binary relations, thentheir composition
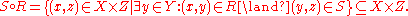
is the relationIn other words,
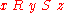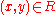is defined by the rule that says if and only if there is an element such that (i.e. and 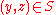).In particular fields, authors might denote by what is defined here to be .
The convention chosen here is such that function composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
(with the usual notation) is obtained as a special case, when R and S are functional relations. Some authors prefer to write
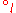and 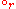explicitly when necessary, depending whether the left or the right relation is the first one applied.A further variation encountered in computer science is the Z notation
Z notation
The Z notation , named after Zermelo–Fraenkel set theory, is a formal specification language used for describing and modelling computing systems. It is targeted at the clear specification of computer programs and computer-based systems in general.-History:...
:
is used to denote the traditional (right) composition, but ⨾ (a fat semicolon with Unicode code point U+2A3E) denotes left composition. This use of semicolon coincides with the notation for function composition used (mostly by computer scientists) in Category theoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
. Because U+2A3E is hard to distinguish from a normal semicolon in some fonts at small sizes, its "capital" version ⨟ (U+2A1F) may be preferable in some fonts. In non-Unicode LaTeX
LaTeX
LaTeX is a document markup language and document preparation system for the TeX typesetting program. Within the typesetting system, its name is styled as . The term LaTeX refers only to the language in which documents are written, not to the editor used to write those documents. In order to...
, the symbol may obtain using the
\fatsemi macro from the stmaryrd package.The binary relations
are sometimes regarded as the morphisms 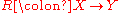in a categoryCategory (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
Rel
Category of relations
In mathematics, the category Rel has the class of sets as objects and binary relations as morphisms.A morphism R : A → B in this category is a relation between the sets A and B, so ....
which has the sets as objects. In Rel, composition of morphisms is exactly composition of relations as defined above. The category Set
Category of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
of sets is a subcategory of Rel that has the same objects but fewer morphisms. A generalization of this is found in the theory of allegories
Allegory (category theory)
In mathematical category theory, an allegory is a category that has some of the structure of the category of sets and binary relations between them. Allegories can be used as an abstraction of categories of relations, and in this sense the theory of allegories is a generalization of relation...
.
Properties
Composition of relations is associative.The inverse relation
Inverse relation
In mathematics, the inverse relation of a binary relation is the relation that occurs when you switch the order of the elements in the relation. For example, the inverse of the relation 'child of' is the relation 'parent of'...
of is
. This property makes the set of all binary relations on a set a semigroup with involution
Semigroup with involution
In mathematics, in semigroup theory, an involution in a semigroup is a transformation of the semigroup which is its own inverse and which is an anti-automorphism of the semigroup. A semigroup in which an involution is defined is called a semigroup with involution...
.
The compose of (partial) function
Partial function
In mathematics, a partial function from X to Y is a function ƒ: X' → Y, where X' is a subset of X. It generalizes the concept of a function by not forcing f to map every element of X to an element of Y . If X' = X, then ƒ is called a total function and is equivalent to a function...
s (i.e. functional relations) is again a (partial) function.
If R and S are injective, then is injective, which conversely implies only the injectivity of R.
If R and S are surjective, then is surjective, which conversely implies only the surjectivity of S.
The set of binary relations on a set X (i.e. relations from X to X) together with (left or right) relation composition forms a monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
with zero, where the identity map on X is the neutral element, and the empty set is the zero element
Absorbing element
In mathematics, an absorbing element is a special type of element of a set with respect to a binary operation on that set. The result of combining an absorbing element with any element of the set is the absorbing element itself. In semigroup theory, the absorbing element is called a zero element...
.
Join: another form of composition
Other forms of composition of relations, which apply to general n-place relations instead of binary relations, are found in the join operation of relational algebraRelational algebra
Relational algebra, an offshoot of first-order logic , deals with a set of finitary relations that is closed under certain operators. These operators operate on one or more relations to yield a relation...
. The usual composition of two binary relations as defined here can be obtained by taking their join, leading to a ternary relation, followed by a projection that removes the middle component.