Kruskal-Szekeres coordinates
Encyclopedia
In general relativity
Kruskal–Szekeres coordinates, named for Martin Kruskal
and George Szekeres
, are a coordinate system
for the Schwarzschild geometry for a black hole
. These coordinates have the advantage that they cover the entire spacetime manifold
of the maximally extended Schwarzschild solution and are well-behaved everywhere outside the physical singularity.
Conventions: In this article we will take the metric signature
to be (− + + +), and we will work in unit
s where c
= 1. The gravitational constant
G will be kept explicit. We will denote the characteristic mass of the Schwarzschild geometry by M.
Recall that in Schwarzschild coordinates
, the Schwarzschild metric is given by
,
where
is the line element of the 2-sphere
Kruskal–Szekeres coordinates are defined by replacing t and r by a new time coordinate V and a new radial coordinate U:
for the exterior region
, and:
for the interior region
.
In these coordinates the metric is given by
where r is defined implicitly by the equation
or equivalently by
where W is the Lambert W function.
The location of the event horizon
(r = 2GM) in these coordinates is given by
Note that the metric is perfectly well defined and non-singular at the event horizon.
In the literature the Kruskal-Szekers coordinates sometimes also appear in their lightcone variant:
in which the metric is given by
and r is defined implicitly by the equation
(some sources use an alternate notation where the regular Kruskal-Szekeres coordinates are labeled T and R instead of V and U, and the Kruskal-Szekeres lightcone coordinates are labeled u and v rather than
and 
)
These lightcone coordinates have the useful feature that outgoing null geodesics are given by
, while ingoing null geodesics are given by 
. Furthermore, the (future and past) event horizon(s) are given by the equation 
, and curvature singularity is given by the equation 
.
. The allowed values are
In the maximally extended solution there are actually two singularites at r = 0, one for positive V and one for negative V. The negative V singularity is the time-reversed black hole, sometimes dubbed a white hole
. Particles can escape from a white hole but they can never return.
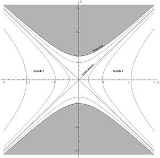
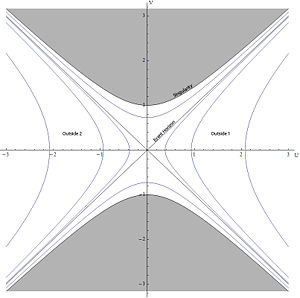
The maximally extended Schwarzschild geometry can be divided into 4 regions each of which can be covered by a suitable set of Schwarzschild coordinates. The
Kruskal–Szekeres coordinates, on the other hand, cover the entire spacetime manifold. The four regions are separated by event horizons.
The transformation given above between Schwarzschild and Kruskal–Szekeres coordinates applies only in regions I and II. A similar transformation can be written down in the other two regions.
The Schwarzschild time coordinate t is given by
In each region it runs from −∞ to +∞ with the infinities at the event horizons.
s of light rays moving in a radial direction) look like straight lines at a 45-degree angle when drawn in a Kruskal-Szekeres diagram (this can be derived from the metric equation given above, which guarantees that if
then 
). All timelike world lines of slower-than-light objects will at every point have a slope closer to the vertical time axis (the V coordinate) than 45 degrees. So, a light cone
drawn in a Kruskal-Szekeres diagram will look just the same as a light cone in a Minkowski diagram
in special relativity
.
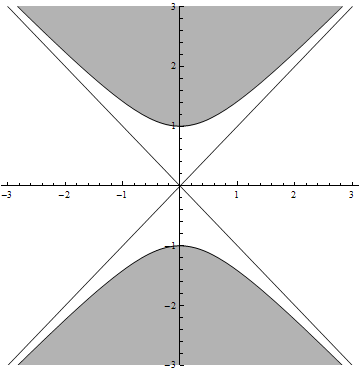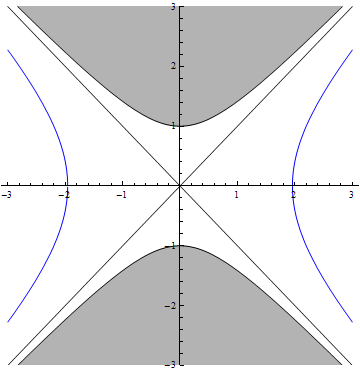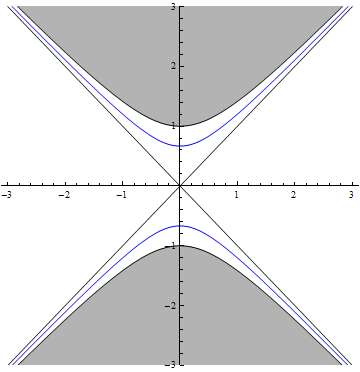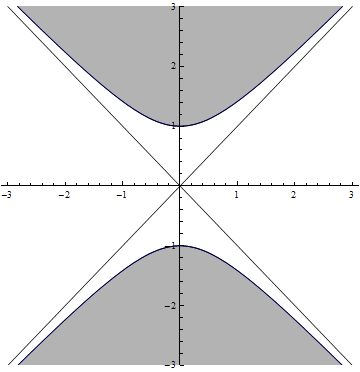
The event horizons bounding the black hole and white hole interior regions are also a pair of straight lines at 45 degrees, reflecting the fact that a light ray emitted at the horizon in a radial direction (aimed outward in the case of the black hole, inward in the case of the white hole) would remain on the horizon forever. Thus the two black hole horizons coincide with the boundaries of the future light cone of an event at the center of the diagram (at U=0 and V=0), while the two white hole horizons coincide with the boundaries of the past light cone of this same event. Any event inside the black hole interior region will have a future light cone that remains in this region (such that any world line within the event's future light cone will eventually hit the black hole singularity, which appears as a hyperbola
bounded by the two black hole horizons), and any event inside the white hole interior region will have a past light cone that remains in this region (such that any world line within this past light cone must have originated in the white hole singularity, a hyperbola bounded by the two white hole horizons).
It may be instructive to consider what curves of constant Schwarzschild coordinate would look like when plotted on a Kruskal-Szekeres diagram. It turns out that curves of constant r-coordinate in Schwarzschild coordinates always look like hyperbolas bounded by a pair of event horizons at 45 degrees, while lines of constant t-coordinate in Schwarzchild coordinates always look like straight lines at various angles passing through the center of the diagram. The black hole event horizon bordering exterior region I would coincide with a Schwarzschild t-coordinate of +∞ while the white hole event horizon bordering this region would coincide with a Schwarzschild t-coordinate of −∞, reflecting the fact that in Schwarzschild coordinates an infalling particle takes an infinite coordinate time to reach the horizon (i.e. the particle's distance from the horizon approaches zero as the Schwarzschild t-coordinate approaches infinity), and a particle traveling up away from the horizon must have crossed it an infinite coordinate time in the past. This is just an artifact of how Schwarzschild coordinates are defined; a free-falling particle will only take a finite proper time
(time as measured by its own clock) to pass between an outside observer and an event horizon, and if the particle's world line is drawn in the Kruskal-Szekeres diagram this will also only take a finite coordinate time in Kruskal-Szekeres coordinates.
The Schwarzschild coordinate system can only cover a single exterior region and a single interior region, such as regions I and II in the Kruskal-Szekeres diagram. The Kruskal-Szekeres coordinate system, on the other hand, can cover a "maximally extended" spacetime which includes the region covered by Schwarzschild coordinates. Here, "maximally extended" refers to the idea that the spacetime should not have any "edges": any geodesic
path can be extended arbitrarily far in either direction unless it runs into a gravitational singularity
. Technically, this means that a maximally extended spacetime is either "geodesically complete" (meaning any geodesic can be extended to arbitrarily large positive or negative values of its 'affine parameter', which in the case of a timelike geodesic could just be the proper time
), or if any geodesics are incomplete, it can only be because they end at a singularity. In order to satisfy this requirement, it was found that in addition to the black hole interior region (region II) which particles enter when they fall through the event horizon from the exterior (region I), there has to be a separate white hole interior region (region IV) which allows us to extend the trajectories of particles which an outside observer sees rising up away from the event horizon, along with a separate exterior region (region III) which allows us to extend some possible particle trajectories in the two interior regions. There are actually multiple possible ways to extend the exterior Schwarzschild solution into a maximally extended spacetime, but the Kruskal-Szekeres extension is unique in that it is a maximal, analytic
, simply connected
vacuum solution
in which all maximally extended geodesics are either complete or else the curvature scalar
diverges along them in finite affine time.
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
Kruskal–Szekeres coordinates, named for Martin Kruskal
Martin Kruskal
Martin David Kruskal was an American mathematician and physicist. He made fundamental contributions in many areas of mathematics and science, ranging from plasma physics to general relativity and from nonlinear analysis to asymptotic analysis...
and George Szekeres
George Szekeres
George Szekeres AM was a Hungarian-Australian mathematician.-Early years:Szekeres was born in Budapest, Hungary as Szekeres György and received his degree in chemistry at the Technical University of Budapest. He worked six years in Budapest as an analytical chemist. He married Esther Klein in 1936...
, are a coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
for the Schwarzschild geometry for a black hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
. These coordinates have the advantage that they cover the entire spacetime manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
of the maximally extended Schwarzschild solution and are well-behaved everywhere outside the physical singularity.
Definition
Metric signature
The signature of a metric tensor is the number of positive and negative eigenvalues of the metric. That is, the corresponding real symmetric matrix is diagonalised, and the diagonal entries of each sign counted...
to be (− + + +), and we will work in unit
Natural units
In physics, natural units are physical units of measurement based only on universal physical constants. For example the elementary charge e is a natural unit of electric charge, or the speed of light c is a natural unit of speed...
s where c
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
= 1. The gravitational constant
Gravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
G will be kept explicit. We will denote the characteristic mass of the Schwarzschild geometry by M.
Recall that in Schwarzschild coordinates
Schwarzschild coordinates
In the theory of Lorentzian manifolds, spherically symmetric spacetimes admit a family of nested round spheres. In such a spacetime, a particularly important kind of coordinate chart is the Schwarzschild chart, a kind of polar spherical coordinate chart on a static and spherically symmetric...
, the Schwarzschild metric is given by,where
is the line element of the 2-sphere
Kruskal–Szekeres coordinates are defined by replacing t and r by a new time coordinate V and a new radial coordinate U:
for the exterior region
, and:for the interior region
.In these coordinates the metric is given by
where r is defined implicitly by the equation
or equivalently by
where W is the Lambert W function.
The location of the event horizon
Event horizon
In general relativity, an event horizon is a boundary in spacetime beyond which events cannot affect an outside observer. In layman's terms it is defined as "the point of no return" i.e. the point at which the gravitational pull becomes so great as to make escape impossible. The most common case...
(r = 2GM) in these coordinates is given by
Note that the metric is perfectly well defined and non-singular at the event horizon.
In the literature the Kruskal-Szekers coordinates sometimes also appear in their lightcone variant:
in which the metric is given by
and r is defined implicitly by the equation
(some sources use an alternate notation where the regular Kruskal-Szekeres coordinates are labeled T and R instead of V and U, and the Kruskal-Szekeres lightcone coordinates are labeled u and v rather than
and )These lightcone coordinates have the useful feature that outgoing null geodesics are given by
, while ingoing null geodesics are given by . Furthermore, the (future and past) event horizon(s) are given by the equation , and curvature singularity is given by the equation .The maximally extended Schwarzschild solution
The transformation between Schwarzschild coordinates and Kruskal–Szekeres coordinates is defined for r > 0, r ≠ 2GM, and −∞ < t < ∞, which is the range for which the Schwarzschild coordinates make sense. However, the coordinates (V, U) can be extended over every value possible without hitting the physical singularityGravitational singularity
A gravitational singularity or spacetime singularity is a location where the quantities that are used to measure the gravitational field become infinite in a way that does not depend on the coordinate system...
. The allowed values are
In the maximally extended solution there are actually two singularites at r = 0, one for positive V and one for negative V. The negative V singularity is the time-reversed black hole, sometimes dubbed a white hole
White hole
A white hole, in general relativity, is a hypothetical region of spacetime which cannot be entered from the outside, but from which matter and light may escape. In this sense it is the reverse of a black hole, which can be entered from the outside, but from which nothing, including light, may escape...
. Particles can escape from a white hole but they can never return.
The maximally extended Schwarzschild geometry can be divided into 4 regions each of which can be covered by a suitable set of Schwarzschild coordinates. The
Kruskal–Szekeres coordinates, on the other hand, cover the entire spacetime manifold. The four regions are separated by event horizons.
| I | exterior region |  and  |
 |
|---|---|---|---|
| II | interior black hole |  and  |
 |
| III | parallel exterior region |  and  |
 |
| IV | interior white hole |  and  |
 |
The transformation given above between Schwarzschild and Kruskal–Szekeres coordinates applies only in regions I and II. A similar transformation can be written down in the other two regions.
The Schwarzschild time coordinate t is given by
In each region it runs from −∞ to +∞ with the infinities at the event horizons.
Qualitative features of the Kruskal-Szekeres diagram
Kruskal-Szekeres coordinates have a number of useful features which make them helpful for building intuitions about the Schwarzschild spacetime. Chief among these is the fact that all radial light-like geodesics (the world lineWorld line
In physics, the world line of an object is the unique path of that object as it travels through 4-dimensional spacetime. The concept of "world line" is distinguished from the concept of "orbit" or "trajectory" by the time dimension, and typically encompasses a large area of spacetime wherein...
s of light rays moving in a radial direction) look like straight lines at a 45-degree angle when drawn in a Kruskal-Szekeres diagram (this can be derived from the metric equation given above, which guarantees that if
then ). All timelike world lines of slower-than-light objects will at every point have a slope closer to the vertical time axis (the V coordinate) than 45 degrees. So, a light coneLight cone
A light cone is the path that a flash of light, emanating from a single event and traveling in all directions, would take through spacetime...
drawn in a Kruskal-Szekeres diagram will look just the same as a light cone in a Minkowski diagram
Minkowski diagram
The Minkowski diagram was developed in 1908 by Hermann Minkowski and provides an illustration of the properties of space and time in the special theory of relativity. It allows a quantitative understanding of the corresponding phenomena like time dilation and length contraction without mathematical...
in special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
.
The event horizons bounding the black hole and white hole interior regions are also a pair of straight lines at 45 degrees, reflecting the fact that a light ray emitted at the horizon in a radial direction (aimed outward in the case of the black hole, inward in the case of the white hole) would remain on the horizon forever. Thus the two black hole horizons coincide with the boundaries of the future light cone of an event at the center of the diagram (at U=0 and V=0), while the two white hole horizons coincide with the boundaries of the past light cone of this same event. Any event inside the black hole interior region will have a future light cone that remains in this region (such that any world line within the event's future light cone will eventually hit the black hole singularity, which appears as a hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
bounded by the two black hole horizons), and any event inside the white hole interior region will have a past light cone that remains in this region (such that any world line within this past light cone must have originated in the white hole singularity, a hyperbola bounded by the two white hole horizons).
It may be instructive to consider what curves of constant Schwarzschild coordinate would look like when plotted on a Kruskal-Szekeres diagram. It turns out that curves of constant r-coordinate in Schwarzschild coordinates always look like hyperbolas bounded by a pair of event horizons at 45 degrees, while lines of constant t-coordinate in Schwarzchild coordinates always look like straight lines at various angles passing through the center of the diagram. The black hole event horizon bordering exterior region I would coincide with a Schwarzschild t-coordinate of +∞ while the white hole event horizon bordering this region would coincide with a Schwarzschild t-coordinate of −∞, reflecting the fact that in Schwarzschild coordinates an infalling particle takes an infinite coordinate time to reach the horizon (i.e. the particle's distance from the horizon approaches zero as the Schwarzschild t-coordinate approaches infinity), and a particle traveling up away from the horizon must have crossed it an infinite coordinate time in the past. This is just an artifact of how Schwarzschild coordinates are defined; a free-falling particle will only take a finite proper time
Proper time
In relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
(time as measured by its own clock) to pass between an outside observer and an event horizon, and if the particle's world line is drawn in the Kruskal-Szekeres diagram this will also only take a finite coordinate time in Kruskal-Szekeres coordinates.
The Schwarzschild coordinate system can only cover a single exterior region and a single interior region, such as regions I and II in the Kruskal-Szekeres diagram. The Kruskal-Szekeres coordinate system, on the other hand, can cover a "maximally extended" spacetime which includes the region covered by Schwarzschild coordinates. Here, "maximally extended" refers to the idea that the spacetime should not have any "edges": any geodesic
Geodesic (general relativity)
In general relativity, a geodesic generalizes the notion of a "straight line" to curved spacetime. Importantly, the world line of a particle free from all external, non-gravitational, force is a particular type of geodesic...
path can be extended arbitrarily far in either direction unless it runs into a gravitational singularity
Gravitational singularity
A gravitational singularity or spacetime singularity is a location where the quantities that are used to measure the gravitational field become infinite in a way that does not depend on the coordinate system...
. Technically, this means that a maximally extended spacetime is either "geodesically complete" (meaning any geodesic can be extended to arbitrarily large positive or negative values of its 'affine parameter', which in the case of a timelike geodesic could just be the proper time
Proper time
In relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
), or if any geodesics are incomplete, it can only be because they end at a singularity. In order to satisfy this requirement, it was found that in addition to the black hole interior region (region II) which particles enter when they fall through the event horizon from the exterior (region I), there has to be a separate white hole interior region (region IV) which allows us to extend the trajectories of particles which an outside observer sees rising up away from the event horizon, along with a separate exterior region (region III) which allows us to extend some possible particle trajectories in the two interior regions. There are actually multiple possible ways to extend the exterior Schwarzschild solution into a maximally extended spacetime, but the Kruskal-Szekeres extension is unique in that it is a maximal, analytic
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
, simply connected
Simply connected space
In topology, a topological space is called simply connected if it is path-connected and every path between two points can be continuously transformed, staying within the space, into any other path while preserving the two endpoints in question .If a space is not simply connected, it is convenient...
vacuum solution
Vacuum solution
A vacuum solution is a solution of a field equation in which the sources of the field are taken to be identically zero. That is, such field equations are written without matter interaction .-Examples:...
in which all maximally extended geodesics are either complete or else the curvature scalar
Scalar curvature
In Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point...
diverges along them in finite affine time.
See also
- Schwarzschild coordinatesSchwarzschild coordinatesIn the theory of Lorentzian manifolds, spherically symmetric spacetimes admit a family of nested round spheres. In such a spacetime, a particularly important kind of coordinate chart is the Schwarzschild chart, a kind of polar spherical coordinate chart on a static and spherically symmetric...
- Eddington-Finkelstein coordinatesEddington-Finkelstein coordinatesIn general relativity Eddington–Finkelstein coordinates, named for Arthur Stanley Eddington and David Finkelstein, are a pair of coordinate systems for a Schwarzschild geometry which are adapted to radial null geodesics...
- Isotropic coordinatesIsotropic coordinatesIn the theory of Lorentzian manifolds, spherically symmetric spacetimes admit a family of nested round spheres. There are several different types of coordinate chart which are adapted to this family of nested spheres; the best known is the Schwarzschild chart, but the isotropic chart is also often...
- Gullstrand-Painlevé coordinatesGullstrand-Painlevé coordinatesGullstrand–Painlevé coordinates were proposed by Paul Painlevé and Allvar Gullstrand in 1921. Similar to Schwarzschild coordinates, GP coordinates can be used in the Schwarzschild metric to describe the space-time physics outside the event horizon of a static black hole. However, Schwarzschild...