Isotropic coordinates
Encyclopedia
In the theory of Lorentzian manifolds, spherically symmetric spacetime
s admit a family of nested round spheres. There are several different types of coordinate chart which are adapted to this family of nested spheres; the best known is the Schwarzschild chart
, but the isotropic chart is also often useful.
The defining characteristic of an isotropic chart is that its radial coordinate (which is different from the radial coordinate of a Schwarschild chart) is defined so that light cones appear round. This means that (except in the trivial case of a locally flat manifold), the angular isotropic coordinates do not faithfully represent distances within the nested spheres, nor does the radial coordinate faithfully represent radial distances. On the other hand, angles in the constant time hyperslices are represented without distortion, hence the name of the chart.
Isotropic charts are most often applied to static
spherically symmetric spacetimes in metric theories of gravitation such as general relativity
, but they can also be used in modeling a spherically pulsating fluid ball, for example. For isolated spherically symmetric solutions of the Einstein field equation, at large distances, the isotropic and Schwarzschild charts become increasingly similar to the usual polar spherical chart on Minkowski spacetime.
takes the form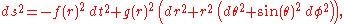
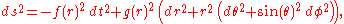
Depending on context, it may be appropriate to regard f,g as undetermined functions of the radial coordinate (for example, in deriving an exact static spherically symmetric solution of the Einstein field equation). Alternatively, we can plug in specific functions (possibly depending on some parameters) to obtain an isotropic coordinate chart on a specific Lorentzian spacetime.
of Killing vector field
s of a spherically symmetric static spacetime takes the same form in the isotropic chart as in the Schwarzschild chart. Namely, this algebra is generated by the timelike irrotational Killing vector field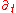
and three spacelike Killing vector fields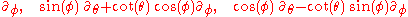
Here, saying that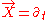
is irrotational means that the vorticity tensor of the corresponding timelike congruence
vanishes; thus, this Killing vector field is hypersurface orthogonal. The fact that the spacetime admits an irrotational timelike Killing vector field is in fact the defining characteristic of a static spacetime
. One immediate consequence is that the constant time coordinate surfaces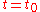
form a family of (isometric) spatial hyperslices (spacelike hypersurfaces).
Unlike the Schwarzschild chart, the isotropic chart is not well suited for constructing embedding diagrams of these hyperslices.
appear as round spheres (when we plot loci in polar spherical fashion), and from the form of the line element, we see that the metric restricted to any of these surfaces is
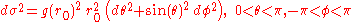
That is, these nested coordinate spheres do in fact represent geometric spheres, but the appearance of
rather than 
shows that the radial coordinate does not correspond to area in the same way as for spheres in ordinary euclidean space
. Compare Schwarschild coordinates, where the radial coordinate does have its natural interpretation in terms of the nested spheres.
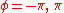mark the boundaries of the isotropic chart, and just as in the Schwarschild chart, we tacitly assume that these two loci are identified, so that our putative round spheres are indeed topological spheres.
Just as for the Schwarschild chart, the range of the radial coordinate may be limited if the metric or its inverse blows up for some value(s) of his coordinate.
in deriving static spherically symmetric solutions in general relativity (or other metric theories of gravitation).
As an illustration, we will sketch how to compute the connection and curvature using Cartan's exterior calculus method. First, we read off the line element a coframe field,
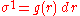
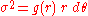
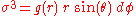
where we regard f,g as undetermined smooth functions of r. (The fact that our spacetime admits a frame having this particular trigonometric form is yet another equivalent expression of the notion of an isotropic chart in a static, spherically symmetric Lorentzian manifold). Taking the exterior derivatives and using the first Cartan structural equation, we find the nonvanishing connection one-forms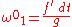
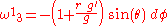
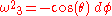
Taking exterior derivatives again and plugging into the second Cartan structural equation, we find the curvature two-forms.
Spherically symmetric spacetime
A spherically symmetric spacetime is a spacetime whose isometry group contains a subgroup which is isomorphic to the group SO and the orbits of this group are 2-dimensional spheres . The isometries are then interpreted as rotations and a spherically symmetric spacetime is often described as one...
s admit a family of nested round spheres. There are several different types of coordinate chart which are adapted to this family of nested spheres; the best known is the Schwarzschild chart
Schwarzschild coordinates
In the theory of Lorentzian manifolds, spherically symmetric spacetimes admit a family of nested round spheres. In such a spacetime, a particularly important kind of coordinate chart is the Schwarzschild chart, a kind of polar spherical coordinate chart on a static and spherically symmetric...
, but the isotropic chart is also often useful.
The defining characteristic of an isotropic chart is that its radial coordinate (which is different from the radial coordinate of a Schwarschild chart) is defined so that light cones appear round. This means that (except in the trivial case of a locally flat manifold), the angular isotropic coordinates do not faithfully represent distances within the nested spheres, nor does the radial coordinate faithfully represent radial distances. On the other hand, angles in the constant time hyperslices are represented without distortion, hence the name of the chart.
Isotropic charts are most often applied to static
Static spacetime
In general relativity, a spacetime is said to be static if it admits a global, non-vanishing, timelike Killing vector field K which is irrotational, i.e., whose orthogonal distribution is involutive...
spherically symmetric spacetimes in metric theories of gravitation such as general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, but they can also be used in modeling a spherically pulsating fluid ball, for example. For isolated spherically symmetric solutions of the Einstein field equation, at large distances, the isotropic and Schwarzschild charts become increasingly similar to the usual polar spherical chart on Minkowski spacetime.
Definition
In an isotropic chart (on a static spherically symmetric spacetime), the line elementLine element
A line element ds in mathematics can most generally be thought of as the change in a position vector in an affine space expressing the change of the arc length. An easy way of visualizing this relationship is by parametrizing the given curve by Frenet–Serret formulas...
takes the form
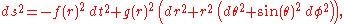
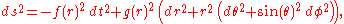
Depending on context, it may be appropriate to regard f,g as undetermined functions of the radial coordinate (for example, in deriving an exact static spherically symmetric solution of the Einstein field equation). Alternatively, we can plug in specific functions (possibly depending on some parameters) to obtain an isotropic coordinate chart on a specific Lorentzian spacetime.
Killing vector fields
The Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of Killing vector field
Killing vector field
In mathematics, a Killing vector field , named after Wilhelm Killing, is a vector field on a Riemannian manifold that preserves the metric. Killing fields are the infinitesimal generators of isometries; that is, flows generated by Killing fields are continuous isometries of the manifold...
s of a spherically symmetric static spacetime takes the same form in the isotropic chart as in the Schwarzschild chart. Namely, this algebra is generated by the timelike irrotational Killing vector field
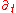
and three spacelike Killing vector fields
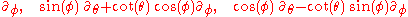
Here, saying that
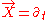is irrotational means that the vorticity tensor of the corresponding timelike congruenceCongruence (general relativity)
In general relativity, a congruence is the set of integral curves of a vector field in a four-dimensional Lorentzian manifold which is interpreted physically as a model of spacetime...
vanishes; thus, this Killing vector field is hypersurface orthogonal. The fact that the spacetime admits an irrotational timelike Killing vector field is in fact the defining characteristic of a static spacetime
Static spacetime
In general relativity, a spacetime is said to be static if it admits a global, non-vanishing, timelike Killing vector field K which is irrotational, i.e., whose orthogonal distribution is involutive...
. One immediate consequence is that the constant time coordinate surfaces
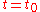form a family of (isometric) spatial hyperslices (spacelike hypersurfaces).Unlike the Schwarzschild chart, the isotropic chart is not well suited for constructing embedding diagrams of these hyperslices.
A family of static nested spheres
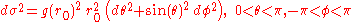
The surfaces appear as round spheres (when we plot loci in polar spherical fashion), and from the form of the line element, we see that the metric restricted to any of these surfaces isThat is, these nested coordinate spheres do in fact represent geometric spheres, but the appearance of
rather than shows that the radial coordinate does not correspond to area in the same way as for spheres in ordinary euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. Compare Schwarschild coordinates, where the radial coordinate does have its natural interpretation in terms of the nested spheres.
Coordinate singularities
The loci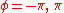 mark the boundaries of the isotropic chart, and just as in the Schwarschild chart, we tacitly assume that these two loci are identified, so that our putative round spheres are indeed topological spheres.Just as for the Schwarschild chart, the range of the radial coordinate may be limited if the metric or its inverse blows up for some value(s) of his coordinate.
A metric Ansatz
The line element given above, with f,g, regarded as undetermined functions of the isotropic coordinate r, is often used as a metric AnsatzAnsatz
Ansatz is a German noun with several meanings in the English language.It is widely encountered in physics and mathematics literature.Since ansatz is a noun, in German texts the initial a of this word is always capitalised.-Definition:...
in deriving static spherically symmetric solutions in general relativity (or other metric theories of gravitation).
As an illustration, we will sketch how to compute the connection and curvature using Cartan's exterior calculus method. First, we read off the line element a coframe field,
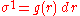
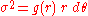
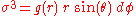
where we regard f,g as undetermined smooth functions of r. (The fact that our spacetime admits a frame having this particular trigonometric form is yet another equivalent expression of the notion of an isotropic chart in a static, spherically symmetric Lorentzian manifold). Taking the exterior derivatives and using the first Cartan structural equation, we find the nonvanishing connection one-forms
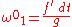
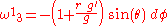
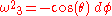
Taking exterior derivatives again and plugging into the second Cartan structural equation, we find the curvature two-forms.
See also
- static spacetimeStatic spacetimeIn general relativity, a spacetime is said to be static if it admits a global, non-vanishing, timelike Killing vector field K which is irrotational, i.e., whose orthogonal distribution is involutive...
, - spherically symmetric spacetimeSpherically symmetric spacetimeA spherically symmetric spacetime is a spacetime whose isometry group contains a subgroup which is isomorphic to the group SO and the orbits of this group are 2-dimensional spheres . The isometries are then interpreted as rotations and a spherically symmetric spacetime is often described as one...
, - static spherically symmetric perfect fluidStatic spherically symmetric perfect fluidIn metric theories of gravitation, particularly general relativity, a static spherically symmetric perfect fluid solution is a spacetime equipped with suitable tensor fields which models a static round ball of a fluid with isotropic pressure.Such solutions are often used as idealized models of...
s, - Schwarzschild coordinatesSchwarzschild coordinatesIn the theory of Lorentzian manifolds, spherically symmetric spacetimes admit a family of nested round spheres. In such a spacetime, a particularly important kind of coordinate chart is the Schwarzschild chart, a kind of polar spherical coordinate chart on a static and spherically symmetric...
, another popular chart for static spherically symmetric spacetimes, - frame fields in general relativityFrame fields in general relativityIn general relativity, a frame field is a set of four orthonormal vector fields, one timelike and three spacelike, defined on a Lorentzian manifold that is physically interpreted as a model of spacetime...
, for more about frame fields and coframe fields.