Charge (physics)
Encyclopedia
In physics
, a charge may refer to one of many different quantities, such as the electric charge
in electromagnetism
or the color charge
in quantum chromodynamics
. Charges are associated with conserved quantum number
s.
of a continuous symmetry
of the physical system under study. When a physical system has a symmetry of some sort, Noether's theorem
implies the existence of a conserved current
. The thing that "flows" in the current is the "charge", the charge is the generator of the (local) symmetry group. This charge is sometimes called the Noether charge.
Thus, for example, the electric charge
is the generator of the U(1) symmetry of electromagnetism
. The conserved current is the electric current
.
In the case of local, dynamical symmetries, associated with every charge is a gauge field; when quantized, the gauge field becomes a gauge boson
. The charges of the theory "radiate" the gauge field. Thus, for example, the gauge field of electromagnetism is the electromagnetic field
; and the gauge boson is the photon
.
Sometimes, the word "charge" is used as a synonym for "generator" in referring to the generator of the symmetry. More precisely, when the symmetry group is a Lie group
, then the charges are understood to correspond to the root system
of the Lie group; the discreteness of the root system accounting for the quantization of the charge.
. These include the charges of the Standard Model
:
Charges of approximate symmetries:
Hypothetical charges of extensions to the Standard Model:
In the formalism of particle theories charge-like quantum numbers can sometimes be inverted by means of a charge conjugation operator called C. Chiral fermions often cannot. Charge conjugation simply means that a given symmetry group occurs in two inequivalent (but still isomorphic) group representation
s. It is usually the case that the two charge-conjugate representations are fundamental representation
s of the Lie group. Their product then forms the adjoint representation
of the group.
Thus, a common example is that the product of two charge-conjugate fundamental representations of SL(2,C) (the spinors) forms the adjoint rep of the Lorentz group
SO(3,1); abstractly, one writes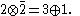
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, a charge may refer to one of many different quantities, such as the electric charge
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
in electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
or the color charge
Color charge
In particle physics, color charge is a property of quarks and gluons that is related to the particles' strong interactions in the theory of quantum chromodynamics . Color charge has analogies with the notion of electric charge of particles, but because of the mathematical complications of QCD,...
in quantum chromodynamics
Quantum chromodynamics
In theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
. Charges are associated with conserved quantum number
Quantum number
Quantum numbers describe values of conserved quantities in the dynamics of the quantum system. Perhaps the most peculiar aspect of quantum mechanics is the quantization of observable quantities. This is distinguished from classical mechanics where the values can range continuously...
s.
Formal definition
More abstractly, a charge is any generatorGenerating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
of a continuous symmetry
Continuous symmetry
In mathematics, continuous symmetry is an intuitive idea corresponding to the concept of viewing some symmetries as motions, as opposed to e.g. reflection symmetry, which is invariance under a kind of flip from one state to another. It has largely and successfully been formalised in the...
of the physical system under study. When a physical system has a symmetry of some sort, Noether's theorem
Noether's theorem
Noether's theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918...
implies the existence of a conserved current
Conserved current
In physics a conserved current is a current, j^\mu, that satisfies the continuity equation \partial_\mu j^\mu=0. The continuity equation represents a conservation law, hence the name....
. The thing that "flows" in the current is the "charge", the charge is the generator of the (local) symmetry group. This charge is sometimes called the Noether charge.
Thus, for example, the electric charge
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
is the generator of the U(1) symmetry of electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
. The conserved current is the electric current
Electric current
Electric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire...
.
In the case of local, dynamical symmetries, associated with every charge is a gauge field; when quantized, the gauge field becomes a gauge boson
Gauge boson
In particle physics, gauge bosons are bosonic particles that act as carriers of the fundamental forces of nature. More specifically, elementary particles whose interactions are described by gauge theory exert forces on each other by the exchange of gauge bosons, usually as virtual particles.-...
. The charges of the theory "radiate" the gauge field. Thus, for example, the gauge field of electromagnetism is the electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
; and the gauge boson is the photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
.
Sometimes, the word "charge" is used as a synonym for "generator" in referring to the generator of the symmetry. More precisely, when the symmetry group is a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
, then the charges are understood to correspond to the root system
Root system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
of the Lie group; the discreteness of the root system accounting for the quantization of the charge.
Examples
Various charge quantum numbers have been introduced by theories of particle physicsParticle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
. These include the charges of the Standard Model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
:
- The color chargeColor chargeIn particle physics, color charge is a property of quarks and gluons that is related to the particles' strong interactions in the theory of quantum chromodynamics . Color charge has analogies with the notion of electric charge of particles, but because of the mathematical complications of QCD,...
of quarks. The color charge generates the SU(3) color symmetry of quantum chromodynamicsQuantum chromodynamicsIn theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
. - The weak isospinWeak isospinIn particle physics, weak isospin is a quantum number relating to the weak interaction, and parallels the idea of isospin under the strong interaction. Weak isospin is usually given the symbol T or I with the third component written as Tz, T3, Iz or I3...
quantum numbers of the electroweak interactionElectroweak interactionIn particle physics, the electroweak interaction is the unified description of two of the four known fundamental interactions of nature: electromagnetism and the weak interaction. Although these two forces appear very different at everyday low energies, the theory models them as two different...
. It generates the SU(2) part of the electroweak SU(2) × U(1) symmetry. Weak isospin is a local symmetry, whose gauge bosonGauge bosonIn particle physics, gauge bosons are bosonic particles that act as carriers of the fundamental forces of nature. More specifically, elementary particles whose interactions are described by gauge theory exert forces on each other by the exchange of gauge bosons, usually as virtual particles.-...
s are the W and Z bosonsW and Z bosonsThe W and Z bosons are the elementary particles that mediate the weak interaction; their symbols are , and . The W bosons have a positive and negative electric charge of 1 elementary charge respectively and are each other's antiparticle. The Z boson is electrically neutral and its own...
. - The electric chargeElectric chargeElectric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
for electromagnetic interactions.
Charges of approximate symmetries:
- The strong isospin charges. The symmetry groups is SU(2) flavor symmetry; the gauge bosons are the pionPionIn particle physics, a pion is any of three subatomic particles: , , and . Pions are the lightest mesons and they play an important role in explaining the low-energy properties of the strong nuclear force....
s. The pions are not fundamental particles, and the symmetry is only approximate. It is a special case of flavor symmetry. - Particle flavor charges, such as strangenessStrangenessIn particle physics, strangeness S is a property of particles, expressed as a quantum number, for describing decay of particles in strong and electromagnetic reactions, which occur in a short period of time...
or charm. These generate the global SU(6) flavor symmetry of the fundamental particles; this symmetry is badly broken by the masses of the heavy quarks.
Hypothetical charges of extensions to the Standard Model:
- The magnetic charge, another charge in the theory of electromagnetism. Magnetic charges are not seen experimentally in laboratory experiments, but would be present for theories including magnetic monopoleMagnetic monopoleA magnetic monopole is a hypothetical particle in particle physics that is a magnet with only one magnetic pole . In more technical terms, a magnetic monopole would have a net "magnetic charge". Modern interest in the concept stems from particle theories, notably the grand unified and superstring...
s.
In the formalism of particle theories charge-like quantum numbers can sometimes be inverted by means of a charge conjugation operator called C. Chiral fermions often cannot. Charge conjugation simply means that a given symmetry group occurs in two inequivalent (but still isomorphic) group representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
s. It is usually the case that the two charge-conjugate representations are fundamental representation
Fundamental representation
In representation theory of Lie groups and Lie algebras, a fundamental representation is an irreducible finite-dimensional representation of a semisimple Lie group...
s of the Lie group. Their product then forms the adjoint representation
Adjoint representation
In mathematics, the adjoint representation of a Lie group G is the natural representation of G on its own Lie algebra...
of the group.
Thus, a common example is that the product of two charge-conjugate fundamental representations of SL(2,C) (the spinors) forms the adjoint rep of the Lorentz group
Lorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
SO(3,1); abstractly, one writes