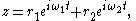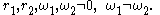Centered trochoid
Encyclopedia
In geometry
, a centered trochoid is the roulette
formed by a circle rolling along another circle. That is, the path traced by a point attached to a circle as the circle rolls without slipping along a fixed circle. The term encompasses both epitrochoid
and hypotrochoid
. The center of this curve is defined to be the center of the fixed circle.
Alternatively, a centered trochoid can be defined as the path traced by the sum of two vectors, each moving at a uniform speed in a circle. Specifically, a centered trochoid is a curve that can be parameterized in the complex plane
by
or in the Cartesian plane by
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a centered trochoid is the roulette
Roulette (curve)
In the differential geometry of curves, a roulette is a kind of curve, generalizing cycloids, epicycloids, hypocycloids, trochoids, and involutes....
formed by a circle rolling along another circle. That is, the path traced by a point attached to a circle as the circle rolls without slipping along a fixed circle. The term encompasses both epitrochoid
Epitrochoid
An epitrochoid is a roulette traced by a point attached to a circle of radius r rolling around the outside of a fixed circle of radius R, where the point is a distance d from the center of the exterior circle....
and hypotrochoid
Hypotrochoid
A hypotrochoid is a roulette traced by a point attached to a circle of radius r rolling around the inside of a fixed circle of radius R, where the point is a distance d from the center of the interior circle....
. The center of this curve is defined to be the center of the fixed circle.
Alternatively, a centered trochoid can be defined as the path traced by the sum of two vectors, each moving at a uniform speed in a circle. Specifically, a centered trochoid is a curve that can be parameterized in the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
by
or in the Cartesian plane by
-
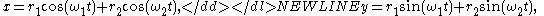
where
If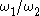 is rational then the curve is closed and algebraic. Otherwise the curve winds around the origin an infinite number of times, and is dense in the annulusAnnulus (mathematics)In mathematics, an annulus is a ring-shaped geometric figure, or more generally, a term used to name a ring-shaped object. Or, it is the area between two concentric circles...
is rational then the curve is closed and algebraic. Otherwise the curve winds around the origin an infinite number of times, and is dense in the annulusAnnulus (mathematics)In mathematics, an annulus is a ring-shaped geometric figure, or more generally, a term used to name a ring-shaped object. Or, it is the area between two concentric circles...
with outer radius and inner radius
and inner radius  .
.
Terminology
Most authors use epitrochoid to mean a roulette of a circle rolling around the outside of another circle, hypotrochoid to mean a roulette of a circle rolling around the inside of another circle, and trochoid to mean a roulette of a circle rolling along a line. However, some authors (for example http://www.monmouth.com/~chenrich/Trochoids/Trochoids.html following F. MorleyFrank MorleyFrank Morley was a leading mathematician, known mostly for his teaching and research in the fields of algebra and geometry...
) use "trochoid" to mean a roulette of a circle rolling along another circle, though this is inconsistent with the more common terminology. The term Centered trochoid as adopted by http://www.mathcurve.com/courbes2d/trochoid/trochoidale.shtml combines epitrochoid and hypotrochoid into a single concept to streamline mathematical exposition and remains consistent with the existing standard.
The term Trochoidal curve describes epitrochoids, hypotrochoids, and trochoids (see http://www.mathcurve.com/courbes2d/trochoid/trochoidale.shtml). A trochoidal curve can be defined as the path traced by the sum of two vectors, each moving at a uniform speed in a circle or in a straight line (but not both moving in a line).
In the parametric equations given above, the curve is an epitrochoid if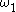 and
and 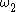 have the same sign, and a hypotrochoid if they have opposite signs.
have the same sign, and a hypotrochoid if they have opposite signs.
Dual generation
Let a circle of radius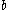 be rolled on a circle of radius
be rolled on a circle of radius  , and a point
, and a point 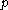 is attached to the rolling circle. The fixed curve can be parameterized as
is attached to the rolling circle. The fixed curve can be parameterized as 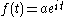 and the rolling curve can be parameterized as either
and the rolling curve can be parameterized as either 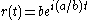 or
or 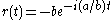 depending on whether the parameterization traverses the circle in the same direction or in the opposite direction as the parameterization of the fixed curve. In either case we may use
depending on whether the parameterization traverses the circle in the same direction or in the opposite direction as the parameterization of the fixed curve. In either case we may use 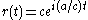 where
where 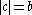 . Let
. Let 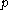 be attached to the rolling circle at
be attached to the rolling circle at 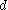 . Then, applying the formula for the rouletteRouletteRoulette is a casino game named after a French diminutive for little wheel. In the game, players may choose to place bets on either a single number or a range of numbers, the colors red or black, or whether the number is odd or even....
. Then, applying the formula for the rouletteRouletteRoulette is a casino game named after a French diminutive for little wheel. In the game, players may choose to place bets on either a single number or a range of numbers, the colors red or black, or whether the number is odd or even....
, the point traces out a curve given by: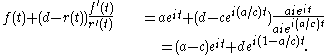
This is the parameterization given above with
 ,
,  ,
,  ,
, 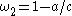 .
.
Conversely, given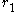 ,
, 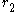 ,
,  , and
, and 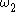 , the curve
, the curve
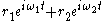 can be reparameterized as
can be reparameterized as
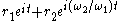 and the equations
and the equations
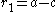 ,
, 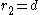 ,
, 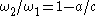
can be solved for ,
,  and
and  to get
to get

The curve remains the same if the indexes
remains the same if the indexes
1 and 2 are reversed but the resulting values of ,
,  and
and 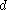 , in general, do not. This produces the Dual generation theorem which states that, with the exception of the special case discussed below, any centered trochoid can be generated in two essentially different ways as the roulette of a circle rolling on another circle.
, in general, do not. This produces the Dual generation theorem which states that, with the exception of the special case discussed below, any centered trochoid can be generated in two essentially different ways as the roulette of a circle rolling on another circle.
Cardioid
The cardioidCardioidA cardioid is a plane curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius. It is therefore a type of limaçon and can also be defined as an epicycloid having a single cusp...
is parameterized by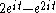 . Take
. Take 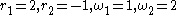 to get
to get  . The circles both have radius 1 and, since c < 0, the rolling circle is rolling around the outside of the fixed circle. The point p is 1 unit from the center of the rolling so it lies on its circumference. This is the usual definition of the cardioid. We may also parameterize the curve as
. The circles both have radius 1 and, since c < 0, the rolling circle is rolling around the outside of the fixed circle. The point p is 1 unit from the center of the rolling so it lies on its circumference. This is the usual definition of the cardioid. We may also parameterize the curve as 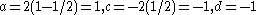 , so we may also take
, so we may also take
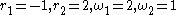
to get
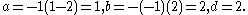 In this case the fixed circle has radius 1, the rolling circle has radius 2, and, since c > 0, the rolling circle revolves around the fixed circle in the fashion of a hula hoopHula hoopA hula hoop is a toy hoop that is twirled around the waist, limbs or neck.Although the exact origins of hula hoops are unknown, children and adults around the world have played with hoops, twirling, rolling and throwing them throughout history...
In this case the fixed circle has radius 1, the rolling circle has radius 2, and, since c > 0, the rolling circle revolves around the fixed circle in the fashion of a hula hoopHula hoopA hula hoop is a toy hoop that is twirled around the waist, limbs or neck.Although the exact origins of hula hoops are unknown, children and adults around the world have played with hoops, twirling, rolling and throwing them throughout history...
. This produces an essentially different definition of the same curve.
Ellipse
If then we obtain the parametric curve
then we obtain the parametric curve 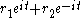 , or
, or
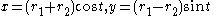 . If
. If 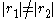 , this is the equation of an ellipseEllipseIn geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
, this is the equation of an ellipseEllipseIn geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
with axes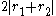 and
and 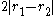 . Evaluating
. Evaluating  ,
,  , and
, and  as before; either
as before; either 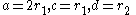 or
or 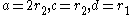 . This gives two different ways of generating an ellipse, both of which involve a circle rolling inside a circle with twice the diameter.
. This gives two different ways of generating an ellipse, both of which involve a circle rolling inside a circle with twice the diameter.
Straight line
If additionally, next to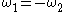 ,
, 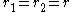 , then
, then 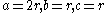 in both cases and the two ways of generating the curve are the same. In this case the curve is simply
in both cases and the two ways of generating the curve are the same. In this case the curve is simply 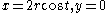 or a segment of the x-axis.
or a segment of the x-axis.
Likewise, if , then
, then 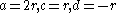 or
or 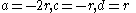 . The circle is symmetric about the origin, so both of these give the same pair of circles. In this case the curve is simply
. The circle is symmetric about the origin, so both of these give the same pair of circles. In this case the curve is simply 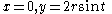 : a segment of the y-axis.
: a segment of the y-axis.
So the case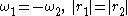 is an exception (in fact the only exception) to the dual generation theorem stated above. This degenerate case, in which the curve is a straight-line segment, underlies the Tusi-coupleTusi-coupleThe Tusi-couple is a mathematical device in which a small circle rotates inside a larger circle twice the diameter of the smaller circle. Rotations of the circles cause a point on the circumference of the smaller circle to oscillate back and forth in linear motion along a diameter of the larger...
is an exception (in fact the only exception) to the dual generation theorem stated above. This degenerate case, in which the curve is a straight-line segment, underlies the Tusi-coupleTusi-coupleThe Tusi-couple is a mathematical device in which a small circle rotates inside a larger circle twice the diameter of the smaller circle. Rotations of the circles cause a point on the circumference of the smaller circle to oscillate back and forth in linear motion along a diameter of the larger...
.
External links
- Introduction and Flash Animation of Epitrochoid (Spanish)
- Introduction and Flash Animation of Hypotrochoid (Spanish)
- Flash Animation of Epitrochoid
- Flash Animation of Hypotrochoid
- Epitrochoid at Mathworld
- Hypotrochoid at Mathworld
- Visual Dictionary of Special Plane Curves
- Visual Dictionary of Special Plane Curves
- "Trochoid" at Springer Online Encyclopaedia of Mathematics
-