Trochoid
Encyclopedia
Gilles de Roberval
Gilles Personne de Roberval , French mathematician, was born at Roberval, Oise, near Beauvais, France. His name was originally Gilles Personne or Gilles Personier, that of Roberval, by which he is known, being taken from the place of his birth.Like René Descartes, he was present at the siege of La...
for the curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
described by a fixed point as a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
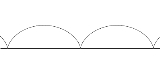
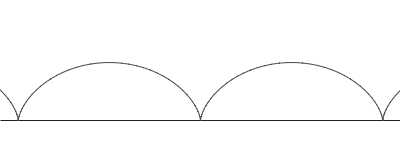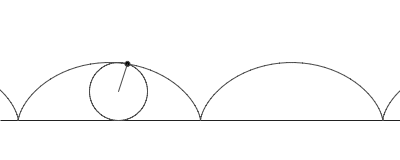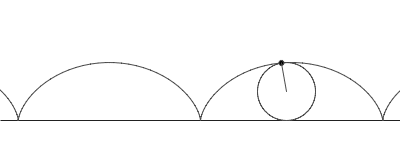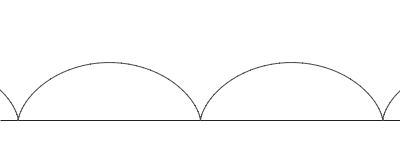
rolls along a straight line. As a circle of radius a rolls without slipping along a line L, the center C moves parallel to L, and every other point P in the rotating plane rigidly attached to the circle traces the curve called the trochoid. Let CP = b. If P lies inside the circle (b < a), on its circumference (b = a), or outside (b > a), the trochoid is described as being curtate, common, or prolate, respectively. Parametric equation
Parametric equation
In mathematics, parametric equation is a method of defining a relation using parameters. A simple kinematic example is when one uses a time parameter to determine the position, velocity, and other information about a body in motion....
s of the trochoid, which assume L is the x-axis, are
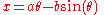
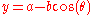
where θ is the variable angle through which the circle rolls. A curtate trochoid is traced by a pedal when a bicycle is pedaled along a straight line. A prolate, or extended trochoid is traced by the tip of a paddle when a boat is driven with constant velocity by paddle wheels; this curve contains loops. A common trochoid, also called a cycloid
Cycloid
A cycloid is the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line.It is an example of a roulette, a curve generated by a curve rolling on another curve....
, has cusp
Cusp (singularity)
In the mathematical theory of singularities a cusp is a type of singular point of a curve. Cusps are local singularities in that they are not formed by self intersection points of the curve....
s at the points where P touches the L.
A more general approach would define a trochoid as the locus
Locus (mathematics)
In geometry, a locus is a collection of points which share a property. For example a circle may be defined as the locus of points in a plane at a fixed distance from a given point....
of a point
orbitingOrbit
In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
at a constant rate around an axis located at
,
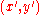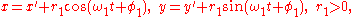
which axis is being translated in the x-y-plane at a constant rate in either a straight line,
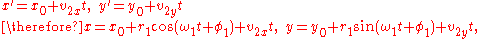
or a circular path (another orbit) around
(the hypotrochoidHypotrochoid
A hypotrochoid is a roulette traced by a point attached to a circle of radius r rolling around the inside of a fixed circle of radius R, where the point is a distance d from the center of the interior circle....
/epitrochoid
Epitrochoid
An epitrochoid is a roulette traced by a point attached to a circle of radius r rolling around the outside of a fixed circle of radius R, where the point is a distance d from the center of the exterior circle....
case),
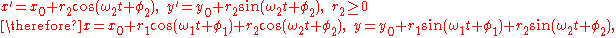
The ratio of the rates of motion and whether the moving axis translates in a straight or circular path determines the shape of the trochoid. In the case of a straight path, one full rotation coincides with one period of a periodic
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
(repeating) locus. In the case of a circular path for the moving axis, the locus is periodic only if the ratio of these angular motions,
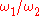, is a rational number, say 
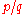, where 
& 
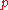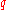are coprimeCoprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
, in which case, one period consists of
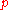orbits around the moving axis and 
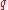orbits of the moving axis around the point 
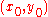. The special cases of the epicycloidEpicycloid
In geometry, an epicycloid is a plane curve produced by tracing the path of a chosen point of a circle — called an epicycle — which rolls without slipping around a fixed circle...
and hypocycloid
Hypocycloid
In geometry, a hypocycloid is a special plane curve generated by the trace of a fixed point on a small circle that rolls within a larger circle...
, generated by tracing the locus of a point on the perimeter of a circle of radius
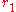while it is rolled on the perimeter of a stationary circle of radius 
, have the following properties: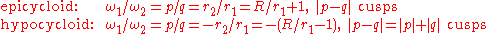
where
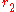is the radius of the orbit of the moving axis. The number of cusps given above also hold true for any epitrochoid and hypotrochoid, with "cusps" replaced by either "radial maxima" or "radial minima."See also
- EpitrochoidEpitrochoidAn epitrochoid is a roulette traced by a point attached to a circle of radius r rolling around the outside of a fixed circle of radius R, where the point is a distance d from the center of the exterior circle....
- HypotrochoidHypotrochoidA hypotrochoid is a roulette traced by a point attached to a circle of radius r rolling around the inside of a fixed circle of radius R, where the point is a distance d from the center of the interior circle....
- CycloidCycloidA cycloid is the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line.It is an example of a roulette, a curve generated by a curve rolling on another curve....
- EpicycloidEpicycloidIn geometry, an epicycloid is a plane curve produced by tracing the path of a chosen point of a circle — called an epicycle — which rolls without slipping around a fixed circle...
- HypocycloidHypocycloidIn geometry, a hypocycloid is a special plane curve generated by the trace of a fixed point on a small circle that rolls within a larger circle...
- SpirographSpirographSpirograph is a geometric drawing toy that produces mathematical curves of the variety technically known as hypotrochoids and epitrochoids. The term has also been used to describe a variety of software applications that display similar curves, and applied to the class of curves that can be produced...
External links
- http://www.xahlee.org/SpecialPlaneCurves_dir/Trochoid_dir/trochoid.html
- Online experiments with the Trochoid using JSXGraph