Proper acceleration
Encyclopedia
In relativity theory, proper acceleration is the physical acceleration (i.e., measurable acceleration as by an accelerometer
) experienced by an object. It is acceleration relative to a free-fall
, or inertial, observer who is momentarily at rest relative to the object being measured. This contrasts with coordinate acceleration, which is dependent on choice of coordinate system
s and thus upon choice of observers.
In the standard inertial coordinates of special relativity, for unidirectional motion, proper acceleration is the rate of change of proper velocity
with respect to coordinate time.
The proper acceleration 3-vector, combined with a null time-component, yields the object's four-acceleration
, which makes proper-acceleration's magnitude Lorentz-invariant. Thus it comes in handy: (i) with accelerated coordinate systems, (ii) at relativistic speeds, and (iii) in curved spacetime.
In an accelerating rocket after launch, or even in a rocket standing at the gantry, the proper acceleration is the acceleration felt by the occupants, and which is described as g-force
(see that article for more discussion of proper acceleration). Neither the acceleration of gravity or "force of gravity" contribute to proper accelerations, and thus the proper acceleration felt by observers standing on the ground is due to the mechanical force from the ground, not due to gravity. If the ground is removed and the observer allowed to fall, the observer will experience coordinate acceleration, but no proper acceleration, and no g-force. Similarly, objects in ballistic paths (in vacuum) and objects in orbit (neglecting tidal forces) experience no proper acceleration. This state is also known as "zero gravity," or "free-fall," and it produces a feeling of weightlessness
.
Proper acceleration reduces to coordinate acceleration
in an inertial coordinate system in flat spacetime (i.e. in the absence of gravity), provided the magnitude of the object's proper-velocity (momentum per unit mass) is much less than the speed of light c. Only in such situations is coordinate acceleration entirely felt as a "g-force" (i.e., a proper acceleration, also defined as one that produces measurable weight).
In situations in which gravitation is absent but the chosen coordinate system is not inertial, but is accelerated with the observer (such as the accelerated reference frame of an accelerating rocket, or a frame fixed upon objects in a centrifuge), then g-forces and corresponding proper accelerations felt by observers in these coordinate systems are caused by the mechanical forces which resist their weight
in such systems. This weight, in turn, is produced by fictitious force
s or "inertial forces" which appear in all such accelerated coordinate systems, in a manner somewhat like the weight produced by the "force of gravity" in systems where objects are fixed in space with regard to the gravitating body (as on the surface of the Earth).
The total (mechanical) force which is calculated to induce the proper acceleration on a mass at rest in a coordinate system that has a proper acceleration, via Newton's law F = m a, is called the proper force. As seen above, the proper force is equal to the opposing reaction force that is measured as an object's "operational weight" (i.e., its weight as measured by a device like a spring scale, in vacuum, in the object's coordinate system). Thus, the proper force on an object is always equal and opposite to its measured weight.
you experience a radially inward (centripetal) proper-acceleration due to the interaction between the hand-hold and your hand. This cancels the radially outward geometric acceleration associated with your spinning coordinate frame
. This outward acceleration (from the spinning frame's perspective) will become the coordinate acceleration when you let go, causing you to fly off along a zero proper-acceleration (geodesic
) path. Unaccelerated observers, of course, in their frame simply see your equal proper and coordinate accelerations vanish when you let go.
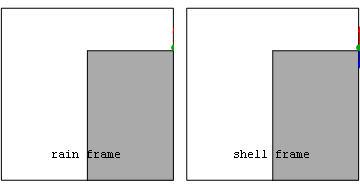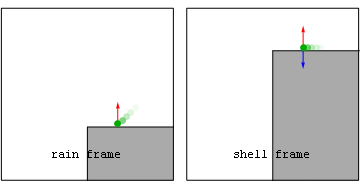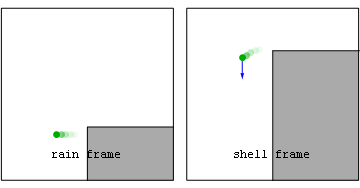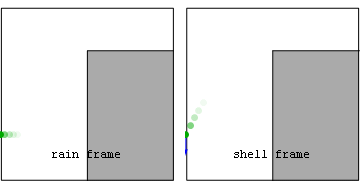
Similarly, standing on a non-rotating planet (and on earth for practical purposes) we experience an upward proper-acceleration due to the normal-force exerted by the earth on the bottom of our shoes. This cancels the downward geometric acceleration due to our choice of coordinate system (a so-called shell-frame). That downward acceleration becomes coordinate if we inadvertently step off a cliff into a zero proper-acceleration (geodesic or rain-frame) trajectory.
Note that geometric accelerations (due to the connection
term in the coordinate system's covariant derivative
below) act on every ounce of our being, while proper-accelerations are usually caused by an external force. Introductory physics courses often treat gravity's downward (geometric) acceleration as one that's due to a mass-proportional force. This, along with diligent avoidance of unaccelerated frames, allows them to treat proper and coordinate acceleration as the same thing.
Even then if an object maintains a constant proper-acceleration from rest over an extended period in flat spacetime, observers in the rest frame will see the object's coordinate acceleration decrease as its coordinate velocity approaches lightspeed. The rate at which the object's proper-velocity goes up, nevertheless, remains constant.
Thus the distinction between proper-acceleration and coordinate acceleration allows one to track the experience of accelerated travelers from various non-Newtonian perspectives. These perspectives include those of accelerated coordinate systems (like a carousel), of high speeds (where proper time differs from coordinate time), and of curved spacetime (like that associated with gravity on earth).
For example, an object subjected to physical or proper acceleration ao will be seen by observers in a coordinate system undergoing constant acceleration aframe to have coordinate acceleration: .
.
Thus if the object is accelerating with the frame, observers fixed to the frame will see no acceleration at all.
Similarly, an object undergoing physical or proper acceleration ao will be seen by observers in a frame rotating with angular velocity ω to have coordinate acceleration: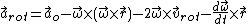 .
.
In the equation above, there are three geometric acceleration terms on the right hand side. The first "centrifugal acceleration" term depends only on the radial position r and not the velocity of our object, the second "Coriolis acceleration" term depends only on the object's velocity in the rotating frame vrot but not its position, and the third "Euler acceleration" term depends only on position and the rate of change of the frame's angular velocity.
In each of these cases, physical or proper acceleration differs from coordinate acceleration because the latter can be affected by your choice of coordinate system as well as by physical forces acting on the object. Those components of coordinate acceleration not caused by physical forces (like direct contact or electrostatic attraction) are often attributed (as in the Newtonian example above) to forces that: (i) act on every ounce of the object, (ii) cause mass-independent accelerations, and (iii) don't exist from all points of view. Such geometric (or improper) forces include Coriolis forces, Euler
forces, g-forces
, centrifugal force
s and (as we see below) gravity forces as well.
's flat-space metric equation (cdτ)2 = (cdt)2 - (dx)2. Here a single reference frame of yardsticks and synchronized clocks define map position x and map time t respectively, the traveling object's clocks define proper time
τ, and the "d" preceding a coordinate means infinitesimal change. These relationships allow one to tackle various problems of "anyspeed engineering", albeit only from the vantage point of an observer whose extended map frame defines simultaneity.
 In the unidirectional case i.e. when the object's acceleration is parallel or anti-parallel to its velocity in the spacetime slice of the observer, proper acceleration α and coordinate acceleration a are related through the Lorentz factor
In the unidirectional case i.e. when the object's acceleration is parallel or anti-parallel to its velocity in the spacetime slice of the observer, proper acceleration α and coordinate acceleration a are related through the Lorentz factor
γ by α=γ3a. Hence the change in proper-velocity w=dx/dτ is the integral of proper acceleration over map-time t i.e. Δw=αΔt for constant α. At low speeds this reduces to the well-known relation
between coordinate velocity
and coordinate acceleration times map-time, i.e. Δv=aΔt.
For constant unidirectional proper-acceleration, similar relationships exist between rapidity
η and elapsed proper time Δτ, as well as between Lorentz factor γ and distance traveled Δx. To be specific:
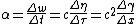 ,
,
where the various velocity parameters are related by .
.
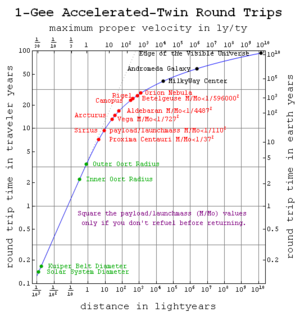
These equations describe some consequences of accelerated travel at high speed. For example, imagine a spaceship that can accelerate its passengers at "1 gee" (or 1.0 lightyears per year squared) halfway to their destination, and then decelerate them at "1 gee" for the remaining half so as to provide earth-like artificial gravity from point A to point B over the shortest possible time. For a map-distance of ΔxAB, the first equation above predicts a mid-point Lorentz factor (up from its unit rest value) of γmid=1+α(ΔxAB/2)/c2. Hence the round-trip time on traveler clocks will be Δτ = 4(c/α) cosh−1(γmid), during which the time elapsed on map clocks will be Δt = 4(c/α) sinh[cosh−1(γmid)].
This imagined spaceship could offer round trips to Proxima Centauri
lasting about 7.1 traveler years (~12 years on Earth clocks), round trips to the Milky Way
's central black hole
of about 40 years (~54,000 years elapsed on earth clocks), and round trips to Andromeda Galaxy
lasting around 57 years (over 5 million years on Earth clocks). Unfortunately, sustaining 1-gee acceleration for years is easier said than done, as illustrated by the maximum payload to launch mass ratios shown in the figure at right.
, the components of an object's acceleration four-vector A (whose magnitude is proper acceleration) are related to elements of the four-velocity
via a covariant derivative
D with respect to proper time τ:
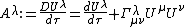
Here U is the object's four-velocity
, and Γ represents the coordinate system's 64 connection coefficients or Christoffel symbols
. Note that the Greek subscripts take on four possible values, namely 0 for the time-axis and 1-3 for spatial coordinate axes, and that repeated indices are used to indicate summation over all values of that index. Trajectories with zero proper acceleration are referred to as geodesic
s.
The left hand side of this set of four equations (one each for the time-like and three spacelike values of index λ) is the object's proper-acceleration 3-vector combined with a null time component as seen from the vantage point of a reference or book-keeper coordinate system. The first term on the right hand side lists the rate at which the time-like (energy/mc) and space-like (momentum/m) components of the object's four-velocity U change, per unit time τ on traveler clocks.
Let's solve for that first term on the right since at low speeds its spacelike components represent the coordinate acceleration. More generally, when that first term goes to zero the object's coordinate acceleration goes to zero. This yields...
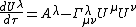 .
.
Thus, as exemplified with the first two animations above, coordinate acceleration goes to zero whenever proper-acceleration is exactly canceled by the connection (or geometric acceleration) term on the far right. Caution: This term may be a sum of as many as sixteen separate velocity and position dependent terms, since the repeated indices μ and ν are by convention summed over all pairs of their four allowed values.
. Consider local book-keeper coordinates for the metric (e.g. a local Lorentz tetrad like that which global positioning system
s provide information on) to describe time in seconds, and space in distance units along perpendicular axes. If we multiply the above equation by the traveling object's rest mass m, and divide by Lorentz factor γ = dt/dτ, the spacelike components express the rate of momentum change for that object from the perspective of the coordinates used to describe the metric.
This in turn can be broken down into parts due to proper and geometric components of acceleration and force. If we further multiply the time-like component by lightspeed c, and define coordinate velocity as v = dx/dt, we get an expression for rate of energy change as well:
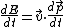 (timelike) and
(timelike) and 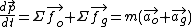 (spacelike).
(spacelike).
Here ao is an acceleration due to proper forces and ag is, by default, a geometric acceleration that we see applied to the object because of our coordinate system choice. At low speeds these accelerations combine to generate a coordinate acceleration like a=d2x/dt2, while for unidirectional motion at any speed ao's magnitude is that of proper acceleration α as in the section above where α = γ3a when ag is zero. In general expressing these accelerations and forces can be complicated.
Nonetheless if we use this breakdown to describe the connection coefficient (Γ) term above in terms of geometric forces, then the motion of objects from the point of view of any coordinate system (at least at low speeds) can be seen as locally Newtonian. This is already common practice e.g. with centrifugal force and gravity. Thus the equivalence principle extends the local usefulness of Newton's laws to accelerated coordinate systems and beyond.
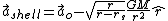
where the planet or star's Schwarzschild radius
rs=2GM/c2. As our shell observer's radius approaches the Schwarzschild radius, the proper acceleration ao needed to keep it from falling in becomes intolerable.
On the other hand for r>>rs, an upward proper force of only GMm/r2 is needed to prevent one from accelerating downward. At the Earth's surface this becomes:
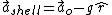
where g is the downward 9.8 m/s2 acceleration due to gravity, and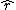 is a unit vector in the radially outward direction from the center of the gravitating body. Thus here an outward proper force of mg is needed to keep one from accelerating downward.
is a unit vector in the radially outward direction from the center of the gravitating body. Thus here an outward proper force of mg is needed to keep one from accelerating downward.
:
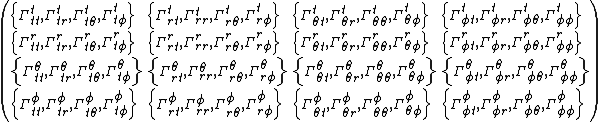
for the far-coordinate Schwarzschild metric
, where rs is the Schwarzschild radius
2GM/c2. The resulting array of coefficients becomes: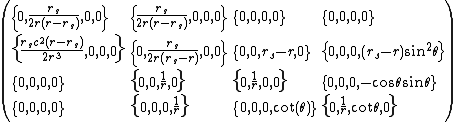 .
.
From this you can obtain the shell-frame proper acceleration by setting coordinate acceleration to zero and thus requiring that proper acceleration cancel the geometric acceleration of a stationary object i.e.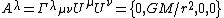 . This does not solve the problem yet, since Schwarzschild coordinates
. This does not solve the problem yet, since Schwarzschild coordinates
in curved spacetime are book-keeper coordinates but not those of a local observer. The magnitude of the above proper acceleration 4-vector, namely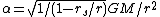 , is however precisely what we want i.e. the upward frame-invariant proper acceleration needed to counteract the downward geometric acceleration felt by dwellers on the surface of a planet.
, is however precisely what we want i.e. the upward frame-invariant proper acceleration needed to counteract the downward geometric acceleration felt by dwellers on the surface of a planet.
A special case of the above Christoffel symbol set is the flat-space spherical coordinate set obtained by setting rs or M above to zero:
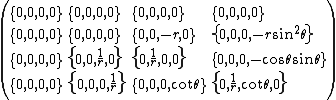 .
.
From this we can obtain, for example, the centripetal proper acceleration needed to cancel the centrifugal geometric acceleration of an object moving at constant angular velocity ω=dφ/dτ at the equator where θ=π/2. Forming the same 4-vector sum as above for the case of dθ/dτ and dr/dτ zero yields nothing more than the classical acceleration for rotational motion given above, i.e. so that ao=ω2r. Coriolis effects also reside in these connection coefficients, and similarly arise from coordinate-frame geometry alone.
so that ao=ω2r. Coriolis effects also reside in these connection coefficients, and similarly arise from coordinate-frame geometry alone.
Accelerometer
An accelerometer is a device that measures proper acceleration, also called the four-acceleration. This is not necessarily the same as the coordinate acceleration , but is rather the type of acceleration associated with the phenomenon of weight experienced by a test mass that resides in the frame...
) experienced by an object. It is acceleration relative to a free-fall
Free-fall
Free fall is any motion of a body where gravity is the only force acting upon it, at least initially. These conditions produce an inertial trajectory so long as gravity remains the only force. Since this definition does not specify velocity, it also applies to objects initially moving upward...
, or inertial, observer who is momentarily at rest relative to the object being measured. This contrasts with coordinate acceleration, which is dependent on choice of coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
s and thus upon choice of observers.
In the standard inertial coordinates of special relativity, for unidirectional motion, proper acceleration is the rate of change of proper velocity
Proper velocity
In relativity, proper-velocity, also known as celerity, is an alternative to velocity for measuring motion. Whereas velocity relative to an observer is distance per unit time where both distance and time are measured by the observer, proper velocity relative to an observer divides observer-measured...
with respect to coordinate time.
The proper acceleration 3-vector, combined with a null time-component, yields the object's four-acceleration
Four-acceleration
In special relativity, four-acceleration is a four-vector and is defined as the change in four-velocity over the particle's proper time:whereandand \gamma_u is the Lorentz factor for the speed u...
, which makes proper-acceleration's magnitude Lorentz-invariant. Thus it comes in handy: (i) with accelerated coordinate systems, (ii) at relativistic speeds, and (iii) in curved spacetime.
In an accelerating rocket after launch, or even in a rocket standing at the gantry, the proper acceleration is the acceleration felt by the occupants, and which is described as g-force
G-force
The g-force associated with an object is its acceleration relative to free-fall. This acceleration experienced by an object is due to the vector sum of non-gravitational forces acting on an object free to move. The accelerations that are not produced by gravity are termed proper accelerations, and...
(see that article for more discussion of proper acceleration). Neither the acceleration of gravity or "force of gravity" contribute to proper accelerations, and thus the proper acceleration felt by observers standing on the ground is due to the mechanical force from the ground, not due to gravity. If the ground is removed and the observer allowed to fall, the observer will experience coordinate acceleration, but no proper acceleration, and no g-force. Similarly, objects in ballistic paths (in vacuum) and objects in orbit (neglecting tidal forces) experience no proper acceleration. This state is also known as "zero gravity," or "free-fall," and it produces a feeling of weightlessness
Weightlessness
Weightlessness is the condition that exists for an object or person when they experience little or no acceleration except the acceleration that defines their inertial trajectory, or the trajectory of pure free-fall...
.
Proper acceleration reduces to coordinate acceleration
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
in an inertial coordinate system in flat spacetime (i.e. in the absence of gravity), provided the magnitude of the object's proper-velocity (momentum per unit mass) is much less than the speed of light c. Only in such situations is coordinate acceleration entirely felt as a "g-force" (i.e., a proper acceleration, also defined as one that produces measurable weight).
In situations in which gravitation is absent but the chosen coordinate system is not inertial, but is accelerated with the observer (such as the accelerated reference frame of an accelerating rocket, or a frame fixed upon objects in a centrifuge), then g-forces and corresponding proper accelerations felt by observers in these coordinate systems are caused by the mechanical forces which resist their weight
Weight
In science and engineering, the weight of an object is the force on the object due to gravity. Its magnitude , often denoted by an italic letter W, is the product of the mass m of the object and the magnitude of the local gravitational acceleration g; thus:...
in such systems. This weight, in turn, is produced by fictitious force
Fictitious force
A fictitious force, also called a pseudo force, d'Alembert force or inertial force, is an apparent force that acts on all masses in a non-inertial frame of reference, such as a rotating reference frame....
s or "inertial forces" which appear in all such accelerated coordinate systems, in a manner somewhat like the weight produced by the "force of gravity" in systems where objects are fixed in space with regard to the gravitating body (as on the surface of the Earth).
The total (mechanical) force which is calculated to induce the proper acceleration on a mass at rest in a coordinate system that has a proper acceleration, via Newton's law F = m a, is called the proper force. As seen above, the proper force is equal to the opposing reaction force that is measured as an object's "operational weight" (i.e., its weight as measured by a device like a spring scale, in vacuum, in the object's coordinate system). Thus, the proper force on an object is always equal and opposite to its measured weight.
Examples
For instance, when holding onto a carousel that turns at constant angular velocityAngular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
you experience a radially inward (centripetal) proper-acceleration due to the interaction between the hand-hold and your hand. This cancels the radially outward geometric acceleration associated with your spinning coordinate frame
Rotating reference frame
A rotating frame of reference is a special case of a non-inertial reference frame that is rotating relative to an inertial reference frame. An everyday example of a rotating reference frame is the surface of the Earth. A rotating frame of reference is a special case of a non-inertial reference...
. This outward acceleration (from the spinning frame's perspective) will become the coordinate acceleration when you let go, causing you to fly off along a zero proper-acceleration (geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
) path. Unaccelerated observers, of course, in their frame simply see your equal proper and coordinate accelerations vanish when you let go.
| Animation: lost grip on a carousel |
|---|
 |
Similarly, standing on a non-rotating planet (and on earth for practical purposes) we experience an upward proper-acceleration due to the normal-force exerted by the earth on the bottom of our shoes. This cancels the downward geometric acceleration due to our choice of coordinate system (a so-called shell-frame). That downward acceleration becomes coordinate if we inadvertently step off a cliff into a zero proper-acceleration (geodesic or rain-frame) trajectory.
| Animation: ball that rolls off a cliff |
|---|
 |
Note that geometric accelerations (due to the connection
Affine connection
In the branch of mathematics called differential geometry, an affine connection is a geometrical object on a smooth manifold which connects nearby tangent spaces, and so permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space...
term in the coordinate system's covariant derivative
Covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
below) act on every ounce of our being, while proper-accelerations are usually caused by an external force. Introductory physics courses often treat gravity's downward (geometric) acceleration as one that's due to a mass-proportional force. This, along with diligent avoidance of unaccelerated frames, allows them to treat proper and coordinate acceleration as the same thing.
Even then if an object maintains a constant proper-acceleration from rest over an extended period in flat spacetime, observers in the rest frame will see the object's coordinate acceleration decrease as its coordinate velocity approaches lightspeed. The rate at which the object's proper-velocity goes up, nevertheless, remains constant.
| Animation: high speed trip up then down |
|---|
 where c is lightspeed and α is the (red) proper acceleration's magnitude. This first leg takes about 2 years if the acceleration's magnitude is about 1-gee. It then accelerates downward (first slowing and then speeding up) over twice that period, followed by a 2*c/α upward deceleration to return to the original height. Note that the coordinate acceleration (green) is significant only during the low-speed segments of this voyage. |
Thus the distinction between proper-acceleration and coordinate acceleration allows one to track the experience of accelerated travelers from various non-Newtonian perspectives. These perspectives include those of accelerated coordinate systems (like a carousel), of high speeds (where proper time differs from coordinate time), and of curved spacetime (like that associated with gravity on earth).
Classical applications
At low speeds in the inertial coordinate systems of Newtonian physics, proper acceleration simply equals the coordinate acceleration a=d2x/dt2. As reviewed above, however, it differs from coordinate acceleration if one chooses (against Newton's advice) to describe the world from the perspective of an accelerated coordinate system like a motor vehicle accelerating from rest, or a stone being spun around in a slingshot. If one chooses to recognize that gravity is caused by the curvature of spacetime (see below), proper acceleration also differs from coordinate acceleration in a gravitational field.For example, an object subjected to physical or proper acceleration ao will be seen by observers in a coordinate system undergoing constant acceleration aframe to have coordinate acceleration:
 .
.Thus if the object is accelerating with the frame, observers fixed to the frame will see no acceleration at all.
| Animation: driving from block to block |
|---|
 |
Similarly, an object undergoing physical or proper acceleration ao will be seen by observers in a frame rotating with angular velocity ω to have coordinate acceleration:
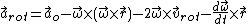 .
.In the equation above, there are three geometric acceleration terms on the right hand side. The first "centrifugal acceleration" term depends only on the radial position r and not the velocity of our object, the second "Coriolis acceleration" term depends only on the object's velocity in the rotating frame vrot but not its position, and the third "Euler acceleration" term depends only on position and the rate of change of the frame's angular velocity.
| Newtonian example: constant speed slingshot |
|---|
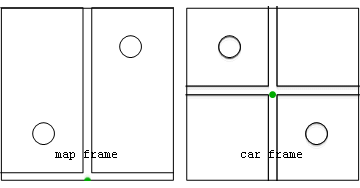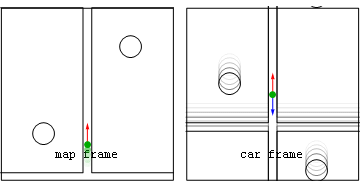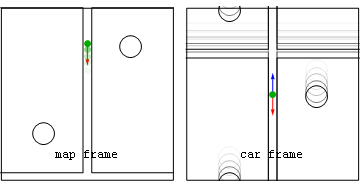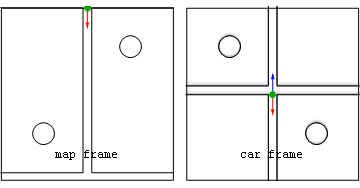
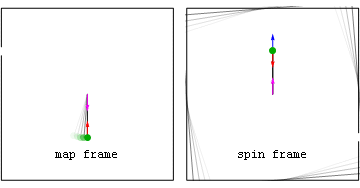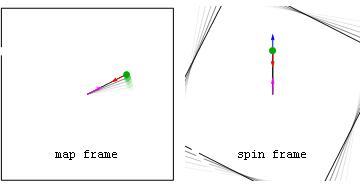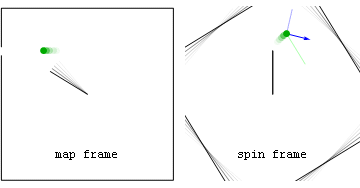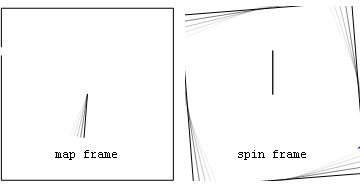 Note that after release in the spin frame that the centrifugal component (light blue) is always radial, while the Coriolis component (green) is always perpendicular to spin frame velocity. Also seen in both frames is the force on the rope's anchor point (magenta) caused by Newton's 3rd Law action-reaction to the centripetal force on the stone. Before projectile launchThe following alternate analyses of motion before the stone is released consider only forces acting in the radial direction. Both analyses predict that string tension T=mv2/r. For example if the radius of the sling is r=1 metre, the velocity of the stone in the map frame is v=25 metres per second, and the stone's mass m=0.2 kilogram, then the tension in the string will be 125 newtons.
Here the stone is seen to be continually accelerated inward so as to follow a circular path of radius r. The inward radial acceleration of aradial=v2/r is caused by a single unbalanced centripetal force T. The fact that the tension force is unbalanced means that, in this frame, the centrifugal (radially-outward) force on the stone is zero.
From the spin frame perspective the stone may be said to experience balanced inward centripetal (T) and outward centrifugal (mv2/r) forces, which result in no acceleration at all from the perspective of that frame. Unlike the centripetal force, the frame-dependent centrifugal force acts on every bit of the circling stone much as gravity acts on every ounce of you. Moreover the centrifugal force magnitude is proportional to the stone's mass so that, if allowed to cause acceleration, the acceleration would be mass-independent. After projectile launchAfter the stone is released, in the spin frame both centripetal and Coriolis forces act in a delocalized way on all parts of the stone with accelerations that are independent of the stone's mass. By comparison in the map frame, after release no forces are acting on the projectile at all. |
In each of these cases, physical or proper acceleration differs from coordinate acceleration because the latter can be affected by your choice of coordinate system as well as by physical forces acting on the object. Those components of coordinate acceleration not caused by physical forces (like direct contact or electrostatic attraction) are often attributed (as in the Newtonian example above) to forces that: (i) act on every ounce of the object, (ii) cause mass-independent accelerations, and (iii) don't exist from all points of view. Such geometric (or improper) forces include Coriolis forces, Euler
Euler force
In classical mechanics, the Euler acceleration , also known as azimuthal acceleration or transverse acceleration is an acceleration that appears when a non-uniformly rotating reference frame is used for analysis of motion and there is variation in the angular velocity of the reference frame's axes...
forces, g-forces
G force
The g-force associated with an object is its acceleration relative to free-fall.It may also refer to:* G-Force , a 2009 film by Disney** G-Force , a 2009 video game based on the film...
, centrifugal force
Centrifugal force
Centrifugal force can generally be any force directed outward relative to some origin. More particularly, in classical mechanics, the centrifugal force is an outward force which arises when describing the motion of objects in a rotating reference frame...
s and (as we see below) gravity forces as well.
Viewed from a flat spacetime slice
Proper-acceleration's relationships to coordinate acceleration in a specified slice of flat spacetime follow from MinkowskiHermann Minkowski
Hermann Minkowski was a German mathematician of Ashkenazi Jewish descent, who created and developed the geometry of numbers and who used geometrical methods to solve difficult problems in number theory, mathematical physics, and the theory of relativity.- Life and work :Hermann Minkowski was born...
's flat-space metric equation (cdτ)2 = (cdt)2 - (dx)2. Here a single reference frame of yardsticks and synchronized clocks define map position x and map time t respectively, the traveling object's clocks define proper time
Proper time
In relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
τ, and the "d" preceding a coordinate means infinitesimal change. These relationships allow one to tackle various problems of "anyspeed engineering", albeit only from the vantage point of an observer whose extended map frame defines simultaneity.
Acceleration in (1+1)D

Lorentz factor
The Lorentz factor or Lorentz term appears in several equations in special relativity, including time dilation, length contraction, and the relativistic mass formula. Because of its ubiquity, physicists generally represent it with the shorthand symbol γ . It gets its name from its earlier...
γ by α=γ3a. Hence the change in proper-velocity w=dx/dτ is the integral of proper acceleration over map-time t i.e. Δw=αΔt for constant α. At low speeds this reduces to the well-known relation
Equation of motion
Equations of motion are equations that describe the behavior of a system in terms of its motion as a function of time...
between coordinate velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
and coordinate acceleration times map-time, i.e. Δv=aΔt.
For constant unidirectional proper-acceleration, similar relationships exist between rapidity
Rapidity
In relativity, rapidity is an alternative to speed as a framework for measuring motion. On parallel velocities rapidities are simply additive, unlike speeds at relativistic velocities. For low speeds, rapidity and speed are proportional, but for high speeds, rapidity takes a larger value. The...
η and elapsed proper time Δτ, as well as between Lorentz factor γ and distance traveled Δx. To be specific:
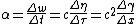 ,
,where the various velocity parameters are related by
 .
.These equations describe some consequences of accelerated travel at high speed. For example, imagine a spaceship that can accelerate its passengers at "1 gee" (or 1.0 lightyears per year squared) halfway to their destination, and then decelerate them at "1 gee" for the remaining half so as to provide earth-like artificial gravity from point A to point B over the shortest possible time. For a map-distance of ΔxAB, the first equation above predicts a mid-point Lorentz factor (up from its unit rest value) of γmid=1+α(ΔxAB/2)/c2. Hence the round-trip time on traveler clocks will be Δτ = 4(c/α) cosh−1(γmid), during which the time elapsed on map clocks will be Δt = 4(c/α) sinh[cosh−1(γmid)].
This imagined spaceship could offer round trips to Proxima Centauri
Proxima Centauri
Proxima Centauri is a red dwarf star about 4.2 light-years distant in the constellation of Centaurus. It was discovered in 1915 by Robert Innes, the Director of the Union Observatory in South Africa, and is the nearest known star to the Sun, although it is too faint to be seen with the naked eye...
lasting about 7.1 traveler years (~12 years on Earth clocks), round trips to the Milky Way
Milky Way
The Milky Way is the galaxy that contains the Solar System. This name derives from its appearance as a dim un-resolved "milky" glowing band arching across the night sky...
's central black hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
of about 40 years (~54,000 years elapsed on earth clocks), and round trips to Andromeda Galaxy
Andromeda Galaxy
The Andromeda Galaxy is a spiral galaxy approximately 2.5 million light-years from Earth in the constellation Andromeda. It is also known as Messier 31, M31, or NGC 224, and is often referred to as the Great Andromeda Nebula in older texts. Andromeda is the nearest spiral galaxy to the...
lasting around 57 years (over 5 million years on Earth clocks). Unfortunately, sustaining 1-gee acceleration for years is easier said than done, as illustrated by the maximum payload to launch mass ratios shown in the figure at right.
| Animation: roundtrip to a star 6.9 ly away |
|---|
 Time dilation In the theory of relativity, time dilation is an observed difference of elapsed time between two events as measured by observers either moving relative to each other or differently situated from gravitational masses. An accurate clock at rest with respect to one observer may be measured to tick at... in action. Other differences include the distance changes between co-moving stars, seen in the traveler frame. This is length contraction Length contraction In physics, length contraction – according to Hendrik Lorentz – is the physical phenomenon of a decrease in length detected by an observer of objects that travel at any non-zero velocity relative to that observer... in action. Coordinate acceleration (green) seen in the map frame is only significant in the year before and after each launch, while the proper-acceleration (red) felt by the traveler is significant throughout the voyage. Note also the trace of a light signal initiated from each launch point, but 0.886 map years after launch. This pulse reaches the traveler at the voyage midpoint to remind them to begin deceleration. In the map frame Proxima Centauri sees the turnaround pulse before the destination star does, but the converse is true in the traveler frame. This is relative simultaneity Relativity of simultaneity In physics, the relativity of simultaneity is the concept that simultaneity–whether two events occur at the same time–is not absolute, but depends on the observer's reference frame. According to the special theory of relativity, it is impossible to say in an absolute sense whether two events occur... in action. Nonetheless both observers agree on the sequence of events along any time-like world line. |
In curved spacetime
In the language of general relativityGeneral relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, the components of an object's acceleration four-vector A (whose magnitude is proper acceleration) are related to elements of the four-velocity
Four-velocity
In physics, in particular in special relativity and general relativity, the four-velocity of an object is a four-vector that replaces classicalvelocity...
via a covariant derivative
Covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
D with respect to proper time τ:
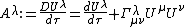
Here U is the object's four-velocity
Four-velocity
In physics, in particular in special relativity and general relativity, the four-velocity of an object is a four-vector that replaces classicalvelocity...
, and Γ represents the coordinate system's 64 connection coefficients or Christoffel symbols
Christoffel symbols
In mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
. Note that the Greek subscripts take on four possible values, namely 0 for the time-axis and 1-3 for spatial coordinate axes, and that repeated indices are used to indicate summation over all values of that index. Trajectories with zero proper acceleration are referred to as geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
s.
The left hand side of this set of four equations (one each for the time-like and three spacelike values of index λ) is the object's proper-acceleration 3-vector combined with a null time component as seen from the vantage point of a reference or book-keeper coordinate system. The first term on the right hand side lists the rate at which the time-like (energy/mc) and space-like (momentum/m) components of the object's four-velocity U change, per unit time τ on traveler clocks.
Let's solve for that first term on the right since at low speeds its spacelike components represent the coordinate acceleration. More generally, when that first term goes to zero the object's coordinate acceleration goes to zero. This yields...
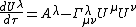 .
.Thus, as exemplified with the first two animations above, coordinate acceleration goes to zero whenever proper-acceleration is exactly canceled by the connection (or geometric acceleration) term on the far right. Caution: This term may be a sum of as many as sixteen separate velocity and position dependent terms, since the repeated indices μ and ν are by convention summed over all pairs of their four allowed values.
Force and equivalence
The above equation also offers some perspective on forces and the equivalence principleEquivalence principle
In the physics of general relativity, the equivalence principle is any of several related concepts dealing with the equivalence of gravitational and inertial mass, and to Albert Einstein's assertion that the gravitational "force" as experienced locally while standing on a massive body is actually...
. Consider local book-keeper coordinates for the metric (e.g. a local Lorentz tetrad like that which global positioning system
Global Positioning System
The Global Positioning System is a space-based global navigation satellite system that provides location and time information in all weather, anywhere on or near the Earth, where there is an unobstructed line of sight to four or more GPS satellites...
s provide information on) to describe time in seconds, and space in distance units along perpendicular axes. If we multiply the above equation by the traveling object's rest mass m, and divide by Lorentz factor γ = dt/dτ, the spacelike components express the rate of momentum change for that object from the perspective of the coordinates used to describe the metric.
This in turn can be broken down into parts due to proper and geometric components of acceleration and force. If we further multiply the time-like component by lightspeed c, and define coordinate velocity as v = dx/dt, we get an expression for rate of energy change as well:
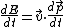 (timelike) and
(timelike) and 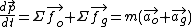 (spacelike).
(spacelike).Here ao is an acceleration due to proper forces and ag is, by default, a geometric acceleration that we see applied to the object because of our coordinate system choice. At low speeds these accelerations combine to generate a coordinate acceleration like a=d2x/dt2, while for unidirectional motion at any speed ao's magnitude is that of proper acceleration α as in the section above where α = γ3a when ag is zero. In general expressing these accelerations and forces can be complicated.
Nonetheless if we use this breakdown to describe the connection coefficient (Γ) term above in terms of geometric forces, then the motion of objects from the point of view of any coordinate system (at least at low speeds) can be seen as locally Newtonian. This is already common practice e.g. with centrifugal force and gravity. Thus the equivalence principle extends the local usefulness of Newton's laws to accelerated coordinate systems and beyond.
Surface dwellers on a planet
For low speed observers being held at fixed radius from the center of a spherical planet or star, coordinate acceleration ashell is approximately related to proper acceleration ao by: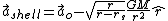
where the planet or star's Schwarzschild radius
Schwarzschild radius
The Schwarzschild radius is the distance from the center of an object such that, if all the mass of the object were compressed within that sphere, the escape speed from the surface would equal the speed of light...
rs=2GM/c2. As our shell observer's radius approaches the Schwarzschild radius, the proper acceleration ao needed to keep it from falling in becomes intolerable.
On the other hand for r>>rs, an upward proper force of only GMm/r2 is needed to prevent one from accelerating downward. At the Earth's surface this becomes:
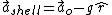
where g is the downward 9.8 m/s2 acceleration due to gravity, and
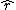 is a unit vector in the radially outward direction from the center of the gravitating body. Thus here an outward proper force of mg is needed to keep one from accelerating downward.
is a unit vector in the radially outward direction from the center of the gravitating body. Thus here an outward proper force of mg is needed to keep one from accelerating downward.Four-vector derivations
The spacetime equations of this section allow one to address all deviations between proper and coordinate acceleration in a single calculation. For example, let's calculate the Christoffel symbolsChristoffel symbols
In mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
:
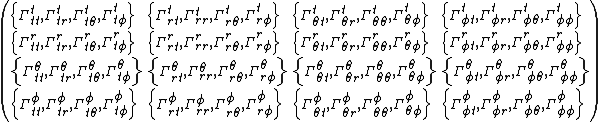
for the far-coordinate Schwarzschild metric
Schwarzschild metric
In Einstein's theory of general relativity, the Schwarzschild solution describes the gravitational field outside a spherical, uncharged, non-rotating mass such as a star, planet, or black hole. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth or...
, where rs is the Schwarzschild radius
Schwarzschild radius
The Schwarzschild radius is the distance from the center of an object such that, if all the mass of the object were compressed within that sphere, the escape speed from the surface would equal the speed of light...
2GM/c2. The resulting array of coefficients becomes:
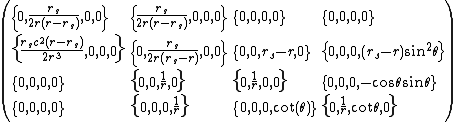 .
.From this you can obtain the shell-frame proper acceleration by setting coordinate acceleration to zero and thus requiring that proper acceleration cancel the geometric acceleration of a stationary object i.e.
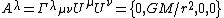 . This does not solve the problem yet, since Schwarzschild coordinates
. This does not solve the problem yet, since Schwarzschild coordinatesSchwarzschild coordinates
In the theory of Lorentzian manifolds, spherically symmetric spacetimes admit a family of nested round spheres. In such a spacetime, a particularly important kind of coordinate chart is the Schwarzschild chart, a kind of polar spherical coordinate chart on a static and spherically symmetric...
in curved spacetime are book-keeper coordinates but not those of a local observer. The magnitude of the above proper acceleration 4-vector, namely
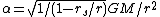 , is however precisely what we want i.e. the upward frame-invariant proper acceleration needed to counteract the downward geometric acceleration felt by dwellers on the surface of a planet.
, is however precisely what we want i.e. the upward frame-invariant proper acceleration needed to counteract the downward geometric acceleration felt by dwellers on the surface of a planet.A special case of the above Christoffel symbol set is the flat-space spherical coordinate set obtained by setting rs or M above to zero:
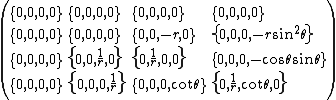 .
.From this we can obtain, for example, the centripetal proper acceleration needed to cancel the centrifugal geometric acceleration of an object moving at constant angular velocity ω=dφ/dτ at the equator where θ=π/2. Forming the same 4-vector sum as above for the case of dθ/dτ and dr/dτ zero yields nothing more than the classical acceleration for rotational motion given above, i.e.
 so that ao=ω2r. Coriolis effects also reside in these connection coefficients, and similarly arise from coordinate-frame geometry alone.
so that ao=ω2r. Coriolis effects also reside in these connection coefficients, and similarly arise from coordinate-frame geometry alone.See also
- KinematicsKinematicsKinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....
: for studying ways that position changes with time - Uniform acceleration: holding coordinate acceleration fixed
- Four-vectorFour-vectorIn the theory of relativity, a four-vector is a vector in a four-dimensional real vector space, called Minkowski space. It differs from a vector in that it can be transformed by Lorentz transformations. The usage of the four-vector name tacitly assumes that its components refer to a standard basis...
: making the connection between space and time explicit - Fictitious forceFictitious forceA fictitious force, also called a pseudo force, d'Alembert force or inertial force, is an apparent force that acts on all masses in a non-inertial frame of reference, such as a rotating reference frame....
: one name for mass times geometric acceleration
External links
- Excerpts from the first edition of Spacetime Physics, and other resources posted by Edwin F. Taylor
- James Hartle's gravity book page including Mathematica programs to calculate Christoffel symbols.
- Andrew Hamilton's notes and programs for working with local tetrads at U. Colorado, Boulder.