Pp-wave spacetime
Encyclopedia
In general relativity
, the pp-wave spacetimes, or pp-waves for short, are an important family of exact solutions of Einstein's field equation. These solutions model radiation
moving at the speed of light
. This radiation may consist of:
or any combination of these, so long as the radiation is all moving in the same direction.
A special type of pp-wave spacetime, the plane wave spacetimes,
provide the most general analog in general relativity of the plane waves
familiar to students of electromagnetism
.
In particular, in general relativity, we must take into account the gravitational effects
of the energy density of the electromagnetic field
itself. When we do this,
purely electromagnetic plane waves provide the direct generalization of ordinary
plane wave solutions in Maxwell's theory.
Furthermore, in general relativity, disturbances in the gravitational field itself can
propagate, at the speed of light, as "wrinkles" in the curvature of spacetime. Such
gravitational radiation is the gravitational field analog of electromagnetic radiation.
In general relativity, the gravitational analogue of electromagnetic plane waves
are precisely the vacuum solutions
among the plane wave spacetimes.
They are called gravitational plane wave
s.
There are physically important examples of pp-wave spacetimes which are not
plane wave spacetimes.
In particular, the physical experience of an observer who whizzes by a gravitating object
(such as a star or a black hole) at nearly the speed of light can be modelled by an
impulsive pp-wave spacetime called the Aichelburg-Sexl ultraboost
.
The gravitational field of a beam of light is modelled, in general relativity, by a certain
axi-symmetric pp-wave.
Pp-waves were introduced by Hans Brinkmann in 1925 and have been rediscovered many times since, most notably by Albert Einstein
and Nathan Rosen
in 1937.
The term pp stands for plane-fronted waves with parallel propagation, and was introduced in 1962 by Jürgen Ehlers
and Wolfgang Kundt.
can be described, with respect to
Brinkmann coordinates
, in the form
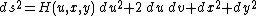
where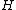
is any smooth function
. This was the original definition of Brinkmann, and it has the virtue of being easy to understand.
The definition which is now standard in the literature is more sophisticated.
It makes no reference to any coordinate chart, so it is a coordinate-free definition.
It states that any Lorentzian manifold which admits a covariantly constant null vector
field
is called a pp-wave spacetime. That is, the covariant derivative
of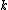
must vanish identically:
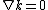
This definition was introduced by Ehlers and Kundt in 1962. To relate Brinkmann's definition to this one, take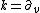
, the coordinate vector
orthogonal to the hypersurfaces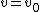
. In the index-gymnastics notation for tensor equations, the condition on 
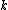can be written 
.
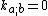Neither of these definitions make any mention of any field equation; in fact,
they are entirely independent of physics. In this sense, the notion of a pp-wave spacetime is entirely mathematical and belongs to the study of
pseudo-Riemannian geometry
.
In the next section, we will turn to the physical interpretation of pp-waves.
Ehlers and Kundt gave several more coordinate-free characterizations, including:
of the Einstein tensor
of any pp-wave spacetime vanishes identically. Equivalently, we can find a Newman/Penrose tetrad such that the Ricci spinor (describing any matter or nongravitational fields which may be present in a spacetime)
and the Weyl spinor (describing any gravitational field which may be present)
each have only one nonvanishing component.
Specifically, with respect to the NP tetrad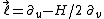
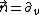
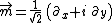
the only nonvanishing component of the Ricci spinor is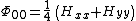
and the only nonvanishing component of the Weyl spinor is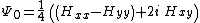
This means that any pp-wave spacetime can be interpreted, in the context of general relativity,
as a null dust solution
. Also, the Weyl tensor
always has Petrov type
N as may be verified by using the Bel criteria.
In other words, pp-waves model various kinds of classical and massless radiation
traveling at the local speed of light
. This radiation can be gravitational, electromagnetic, some hypothetical kind of massless radiation other than these two, or any combination of these. All this radiation is traveling in the same direction, and the null vector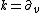
plays the role of a wave vector
.
In any pp-wave spacetime,
the covariantly constant vector field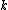
always has identically vanishing optical scalars
. Therefore, pp-waves belong to the Kundt class
(the class of Lorentzian manifolds admitting a null congruence with vanishing optical scalars).
Going in the other direction, pp-waves include several important special cases.
From the form of Ricci spinor given in the preceding section, it is immediately apparent that a pp-wave spacetime (written in the Brinkmann chart) is a vacuum solution
if and only if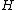
is a harmonic function
(with respect to the spatial coordinates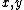
). Physically, these represent purely gravitational radiation propagating along the null rays 
.
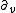Ehlers and Kundt and Sippel and Gönner have classified vacuum pp-wave spacetimes by their autometry group, or group of self-isometries. This is always a Lie group
, and as usual it is easier to classify the underlying Lie algebras of Killing vector fields. It turns out that the most general pp-wave spacetime has only one Killing vector field, the null geodesic congruence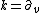
. However, for various special forms of 
, there are additional Killing vector fields.
The most important class of particularly symmetric pp-waves are the plane wave spacetimes, which were first studied by Baldwin and Jeffery.
A plane wave is a pp-wave in which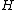
is quadratic, and can hence be transformed to the simple form
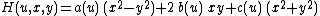
Here,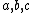
are arbitrary smooth functions of 
.
Physically speaking,
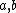describe the wave profiles of the two linearly independent polarization modes of gravitational radiation which may be present,
while
describes the wave profile of any nongravitational radiation.
If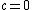
, we have the vacuum plane waves, which are often called plane gravitational waves.
Equivalently, a plane-wave is a pp-wave with at least a five dimensional Lie algebra of Killing vector fields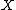
, including 
and four more which have the form
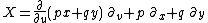
where
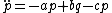
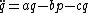
Intuitively, the distinction is that the wavefronts of plane waves are truly planar; all points on a given two-dimensional wavefront are equivalent. This not quite true for more general pp-waves.
Plane waves are important for many reasons; to mention just one, they are essential
for the beautiful topic of colliding plane waves.
A more general subclass consists of the axisymmetric pp-waves, which in general have a two dimensional Abelian
Lie algebra of Killing vector fields.
These are also called SG2 plane waves, because they are the second type in the symmetry
classification of Sippel and Gönner.
A limiting case of certain axisymmetric pp-waves yields
the Aichelburg/Sexl ultraboost modeling an ultrarelativistic encounter with an isolated spherically
symmetric object.
(See also the article on plane wave spacetimes for a discussion of physically important special cases
of plane waves.)
J. D. Steele has introduced the notion of generalised pp-wave spacetimes.
These are nonflat Lorentzian spacetimes which admit a self-dual covariantly constant null bivector field.
The name is potentially misleading, since as Steele points out, these are nominally a special case of nonflat pp-waves in the sense defined above. They are only a generalization in the sense that although the Brinkmann metric form is preserved, they are not necessarily the vacuum solutions studied by Ehlers and Kundt, Sippel and Gönner, etc.
Another important special class of pp-waves are the sandwich waves. These have vanishing curvature except on some range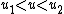
, and represent a gravitational wave moving through a Minkowski spacetime background.
classical field theories of gravitation
. In particular, pp-waves are exact solutions in the
Brans-Dicke theory
,
various higher curvature theories and Kaluza-Klein theories,
and certain gravitation theories of J. W. Moffat.
Indeed, B. O. J. Tupper has shown that the common vacuum solutions in general relativity and in the Brans/Dicke theory are precisely the vacuum pp-waves (but the Brans/Dicke theory admits further wavelike solutions). Hans-Jürgen Schmidt has reformulated the theory of (four-dimensional) pp-waves in terms of a two-dimensional metric-dilaton theory of gravity.
Pp-waves also play an important role in the search for quantum gravity
, because as Gary Gibbons
has pointed out, all loop term quantum corrections vanish identically for any pp-wave spacetime. This means that studying tree-level quantizations of pp-wave spacetimes offers a glimpse into the yet unknown world of quantum gravity.
It is natural to generalize pp-waves to higher dimensions, where they enjoy similar properties to those we have discussed. C. M. Hull has shown that such
higher dimensional pp-waves are essential building blocks for eleven-dimensional supergravity
.
Consider an inertial observer in Minkowski spacetime who encounters a sandwich plane wave. Such an observer will experience some interesting optical effects. If he looks into the oncoming wavefronts at distant galaxies which have already encountered the wave, he will see their images undistorted. This must be the case, since he cannot know the wave is coming until it reaches his location, for it is traveling at the speed of light. However, this can be confirmed by direct computation of the optical scalars of the null congruence
. Now suppose that after the wave passes, our observer turns about face and looks through the departing wavefronts at distant galaxies which the wave has not yet reached. Now he sees their optical images sheared and magnified (or demagnified) in a time-dependent manner. If the wave happens to be a polarized gravitational plane wave, he will see circular images alternately squeezed horizontally while expanded vertically, and squeezed vertically while expanded horizontally. This directly exhibits the characteristic effect of a gravitational wave in general relativity on light.
The effect of a passing polarized gravitational plane wave on the relative positions of a cloud of (initially static) test particles will be qualitatively very similar. We might mention here that in general, the motion of test particles in pp-wave spacetimes can exhibit chaos
.
The fact that Einstein's field equation is nonlinear is well-known. This implies that if you have two exact solutions, there is almost never any way to linearly superimpose
them. PP waves provide a rare exception to this rule:
if you have two PP waves sharing the same covariantly constant null vector (the same geodesic null congruence, i.e. the same wave vector field), with metric functions
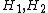respectively, then 
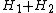gives a third exact solution.
Roger Penrose
has observed that near a null geodesic, every Lorentzian spacetime looks like a plane wave. To show this, he used techniques imported from algebraic geometry to "blow up" the spacetime so that the given null geodesic becomes the covariantly constant null geodesic congruence of a plane wave. This construction is called a Penrose limit.
Penrose also pointed out that in a pp-wave spacetime, all the polynomial scalar invariants of the Riemann tensor
vanish identically, yet the curvature is almost never zero. This is because in four-dimension all pp-waves belong to the class of VSI spacetime
s. Such statement does not hold in higher-dimensions since there are higher-dimensional pp-waves of algebraic type II with non-vanishing polynomial scalar invariants. If you view the Riemann tensor as a second rank tensor acting on bivectors, the vanishing of invariants is analogous to the fact that a nonzero null vector has vanishing squared length.
Penrose was also the first to understand the strange nature of causality in
pp-sandwich wave spacetimes. He showed that some or all of the null geodesics emitted at a given event will be refocused at a later event (or string of events). The details depend upon whether the wave is purely gravitational, purely electromagnetic, or neither.
Every pp-wave admits many different Brinkmann charts. These are related by coordinate transformations, which in this context may be considered to be gauge transformations. In the case of plane waves, these gauge transformations allow us to always regard two colliding plane waves to have parallel wavefronts,
and thus the waves can be said to collide head-on.
This is an exact result in fully nonlinear general relativity which is analogous to a similar result concerning electromagnetic plane wave
s as treated in special relativity
.
("Explicit" means that the metric functions can be written down in terms of elementary functions
or perhaps well-known special functions
such as Mathieu function
s.)
Explicit examples of axisymmetric pp-waves include
Explicit examples of plane wave spacetimes include
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, the pp-wave spacetimes, or pp-waves for short, are an important family of exact solutions of Einstein's field equation. These solutions model radiation
Radiation
In physics, radiation is a process in which energetic particles or energetic waves travel through a medium or space. There are two distinct types of radiation; ionizing and non-ionizing...
moving at the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
. This radiation may consist of:
- electromagnetic radiationElectromagnetic radiationElectromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
, - gravitational radiation,
- massless radiation associated with some hypothetical distinct type relativistic classical field,
or any combination of these, so long as the radiation is all moving in the same direction.
A special type of pp-wave spacetime, the plane wave spacetimes,
provide the most general analog in general relativity of the plane waves
familiar to students of electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
.
In particular, in general relativity, we must take into account the gravitational effects
of the energy density of the electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
itself. When we do this,
purely electromagnetic plane waves provide the direct generalization of ordinary
plane wave solutions in Maxwell's theory.
Furthermore, in general relativity, disturbances in the gravitational field itself can
propagate, at the speed of light, as "wrinkles" in the curvature of spacetime. Such
gravitational radiation is the gravitational field analog of electromagnetic radiation.
In general relativity, the gravitational analogue of electromagnetic plane waves
are precisely the vacuum solutions
Vacuum solution (general relativity)
In general relativity, a vacuum solution is a Lorentzian manifold whose Einstein tensor vanishes identically. According to the Einstein field equation, this means that the stress-energy tensor also vanishes identically, so that no matter or non-gravitational fields are present.More generally, a...
among the plane wave spacetimes.
They are called gravitational plane wave
Gravitational plane wave
In general relativity, a gravitational plane wave is a special class of a vacuum pp-wave spacetime, and may be defined in terms of Brinkmann coordinates byds^2=[a+2bxy]du^2+2dudv+dx^2+dy^2...
s.
There are physically important examples of pp-wave spacetimes which are not
plane wave spacetimes.
In particular, the physical experience of an observer who whizzes by a gravitating object
(such as a star or a black hole) at nearly the speed of light can be modelled by an
impulsive pp-wave spacetime called the Aichelburg-Sexl ultraboost
Aichelburg-Sexl ultraboost
In general relativity, the Aichelburg–Sexl ultraboost is an exact solution which models the physical experience of an observer moving past a spherically symmetric gravitating object at nearly the speed of light. It was introduced by Peter C. Aichelburg and Roman U...
.
The gravitational field of a beam of light is modelled, in general relativity, by a certain
axi-symmetric pp-wave.
Pp-waves were introduced by Hans Brinkmann in 1925 and have been rediscovered many times since, most notably by Albert Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
and Nathan Rosen
Nathan Rosen
Nathan Rosen was an American-Israeli physicist noted for his study on the structure of the hydrogen molecule and his work with Albert Einstein and Boris Podolsky on entangled wave functions and the EPR paradox.-Background:Nathan Rosen was born into a Jewish family in Brooklyn, New York...
in 1937.
The term pp stands for plane-fronted waves with parallel propagation, and was introduced in 1962 by Jürgen Ehlers
Jürgen Ehlers
Jürgen Ehlers was a German physicist who made notable contributions to the current understanding of Albert Einstein's theory of general relativity...
and Wolfgang Kundt.
Mathematical definition
A pp-wave spacetime is any Lorentzian manifold whose metric tensorMetric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
can be described, with respect to
Brinkmann coordinates
Brinkmann coordinates
Brinkmann coordinates are a particular coordinate system for a spacetime belonging to the family of pp-wave metrics. In terms of these coordinates, the metric tensor can be written asds^2 \, = H du^2 + 2 du dv + dx^2 + dy^2...
, in the form
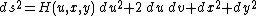
where
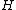is any smooth functionSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
. This was the original definition of Brinkmann, and it has the virtue of being easy to understand.
The definition which is now standard in the literature is more sophisticated.
It makes no reference to any coordinate chart, so it is a coordinate-free definition.
It states that any Lorentzian manifold which admits a covariantly constant null vector
Null vector
Null vector can refer to:* Null vector * A causal structure in Minkowski space...
field
is called a pp-wave spacetime. That is, the covariant derivativeCovariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
of
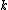must vanish identically: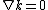This definition was introduced by Ehlers and Kundt in 1962. To relate Brinkmann's definition to this one, take
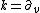, the coordinate vectorCoordinate vector
In linear algebra, a coordinate vector is an explicit representation of a vector in an abstract vector space as an ordered list of numbers or, equivalently, as an element of the coordinate space Fn....
orthogonal to the hypersurfaces
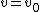. In the index-gymnastics notation for tensor equations, the condition on 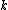can be written 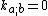.Neither of these definitions make any mention of any field equation; in fact,
they are entirely independent of physics. In this sense, the notion of a pp-wave spacetime is entirely mathematical and belongs to the study of
pseudo-Riemannian geometry
Pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
.
In the next section, we will turn to the physical interpretation of pp-waves.
Ehlers and Kundt gave several more coordinate-free characterizations, including:
- A Lorentzian manifold is a pp-wave if and only if it admits a one-parameter subgroup of isometries having null orbits, and whose curvature tensor has vanishing eigenvalues.
- A Lorentzian manifold with nonvanishing curvature is a (nontrivial) pp-wave if and only if it admits a covariantly constant bivectorBivectorIn mathematics, a bivector or 2-vector is a quantity in geometric algebra or exterior algebra that generalises the idea of a vector. If a scalar is considered a zero dimensional quantity, and a vector is a one dimensional quantity, then a bivector can be thought of as two dimensional. Bivectors...
. (If so, this bivector is a null bivector.)
Physical interpretation
It is a purely mathematical fact that the characteristic polynomialCharacteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of the Einstein tensor
Einstein tensor
In differential geometry, the Einstein tensor , named after Albert Einstein, is used to express the curvature of a Riemannian manifold...
of any pp-wave spacetime vanishes identically. Equivalently, we can find a Newman/Penrose tetrad such that the Ricci spinor (describing any matter or nongravitational fields which may be present in a spacetime)
and the Weyl spinor (describing any gravitational field which may be present)
each have only one nonvanishing component.
Specifically, with respect to the NP tetrad
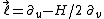
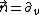
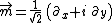
the only nonvanishing component of the Ricci spinor is
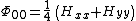
and the only nonvanishing component of the Weyl spinor is
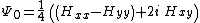
This means that any pp-wave spacetime can be interpreted, in the context of general relativity,
as a null dust solution
Null dust solution
In mathematical physics, a null dust solution is a Lorentzian manifold in which the Einstein tensor is null...
. Also, the Weyl tensor
Weyl tensor
In differential geometry, the Weyl curvature tensor, named after Hermann Weyl, is a measure of the curvature of spacetime or, more generally, a pseudo-Riemannian manifold. Like the Riemann curvature tensor, the Weyl tensor expresses the tidal force that a body feels when moving along a geodesic...
always has Petrov type
Petrov classification
In differential geometry and theoretical physics, the Petrov classification describes the possible algebraic symmetries of the Weyl tensor at each event in a Lorentzian manifold....
N as may be verified by using the Bel criteria.
In other words, pp-waves model various kinds of classical and massless radiation
Radiation
In physics, radiation is a process in which energetic particles or energetic waves travel through a medium or space. There are two distinct types of radiation; ionizing and non-ionizing...
traveling at the local speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
. This radiation can be gravitational, electromagnetic, some hypothetical kind of massless radiation other than these two, or any combination of these. All this radiation is traveling in the same direction, and the null vector
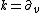plays the role of a wave vectorWave vector
In physics, a wave vector is a vector which helps describe a wave. Like any vector, it has a magnitude and direction, both of which are important: Its magnitude is either the wavenumber or angular wavenumber of the wave , and its direction is ordinarily the direction of wave propagation In...
.
Relation to other classes of exact solutions
Unfortunately, the terminology concerning pp-waves, while fairly standard, is highly confusing and tends to promote misunderstanding.In any pp-wave spacetime,
the covariantly constant vector field
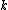always has identically vanishing optical scalarsOptical scalars
In general relativity, optical scalars are a set of scalars that describe various properties of null geodesic congruences. The three optical scalars used in general relativity are expansion, shear and twist and were first defined and used by Sachs...
. Therefore, pp-waves belong to the Kundt class
Kundt spacetime
In mathematical physics, Kundt spacetimes are Lorentzian manifolds admitting a geodesic null congruence with vanishing optical scalars . A well known member of Kundt class is pp-wave. Ricci-flat Kundt spacetimes in arbitrary dimension are algebraically special. In four dimensions Ricci-flat ...
(the class of Lorentzian manifolds admitting a null congruence with vanishing optical scalars).
Going in the other direction, pp-waves include several important special cases.
From the form of Ricci spinor given in the preceding section, it is immediately apparent that a pp-wave spacetime (written in the Brinkmann chart) is a vacuum solution
Vacuum solution
A vacuum solution is a solution of a field equation in which the sources of the field are taken to be identically zero. That is, such field equations are written without matter interaction .-Examples:...
if and only if
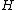is a harmonic functionHarmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
(with respect to the spatial coordinates
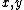). Physically, these represent purely gravitational radiation propagating along the null rays 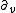.Ehlers and Kundt and Sippel and Gönner have classified vacuum pp-wave spacetimes by their autometry group, or group of self-isometries. This is always a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
, and as usual it is easier to classify the underlying Lie algebras of Killing vector fields. It turns out that the most general pp-wave spacetime has only one Killing vector field, the null geodesic congruence
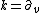. However, for various special forms of , there are additional Killing vector fields.The most important class of particularly symmetric pp-waves are the plane wave spacetimes, which were first studied by Baldwin and Jeffery.
A plane wave is a pp-wave in which
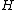is quadratic, and can hence be transformed to the simple form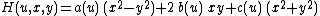Here,
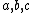are arbitrary smooth functions of .Physically speaking,
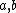describe the wave profiles of the two linearly independent polarization modes of gravitational radiation which may be present,while
describes the wave profile of any nongravitational radiation.If
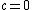, we have the vacuum plane waves, which are often called plane gravitational waves.Equivalently, a plane-wave is a pp-wave with at least a five dimensional Lie algebra of Killing vector fields
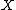, including and four more which have the form
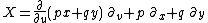
where
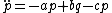
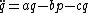
Intuitively, the distinction is that the wavefronts of plane waves are truly planar; all points on a given two-dimensional wavefront are equivalent. This not quite true for more general pp-waves.
Plane waves are important for many reasons; to mention just one, they are essential
for the beautiful topic of colliding plane waves.
A more general subclass consists of the axisymmetric pp-waves, which in general have a two dimensional Abelian
Abelian
In mathematics, Abelian refers to any of number of different mathematical concepts named after Niels Henrik Abel:- Group theory :*Abelian group, a group in which the binary operation is commutative...
Lie algebra of Killing vector fields.
These are also called SG2 plane waves, because they are the second type in the symmetry
classification of Sippel and Gönner.
A limiting case of certain axisymmetric pp-waves yields
the Aichelburg/Sexl ultraboost modeling an ultrarelativistic encounter with an isolated spherically
symmetric object.
(See also the article on plane wave spacetimes for a discussion of physically important special cases
of plane waves.)
J. D. Steele has introduced the notion of generalised pp-wave spacetimes.
These are nonflat Lorentzian spacetimes which admit a self-dual covariantly constant null bivector field.
The name is potentially misleading, since as Steele points out, these are nominally a special case of nonflat pp-waves in the sense defined above. They are only a generalization in the sense that although the Brinkmann metric form is preserved, they are not necessarily the vacuum solutions studied by Ehlers and Kundt, Sippel and Gönner, etc.
Another important special class of pp-waves are the sandwich waves. These have vanishing curvature except on some range
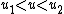, and represent a gravitational wave moving through a Minkowski spacetime background.Relation to other theories
Since they constitute a very simple and natural class of Lorentzian manifolds, defined in terms of a null congruence, it is not very surprising that they are also important in other relativisticTheory of relativity
The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
classical field theories of gravitation
Gravitation
Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
. In particular, pp-waves are exact solutions in the
Brans-Dicke theory
Brans-Dicke theory
In theoretical physics, the Brans–Dicke theory of gravitation is a theoretical framework to explain gravitation. It is a well-known competitor of Einstein's more popular theory of general relativity...
,
various higher curvature theories and Kaluza-Klein theories,
and certain gravitation theories of J. W. Moffat.
Indeed, B. O. J. Tupper has shown that the common vacuum solutions in general relativity and in the Brans/Dicke theory are precisely the vacuum pp-waves (but the Brans/Dicke theory admits further wavelike solutions). Hans-Jürgen Schmidt has reformulated the theory of (four-dimensional) pp-waves in terms of a two-dimensional metric-dilaton theory of gravity.
Pp-waves also play an important role in the search for quantum gravity
Quantum gravity
Quantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...
, because as Gary Gibbons
Gary Gibbons
Gary William Gibbons , FRS, is a British theoretical physicist. Gibbons studied in Cambridge,where in 1969 he became a research student under the supervision of Dennis Sciama. When Sciama moved to Oxford, he became a student of Stephen Hawking, obtaining his PhD from Cambridge in 1973...
has pointed out, all loop term quantum corrections vanish identically for any pp-wave spacetime. This means that studying tree-level quantizations of pp-wave spacetimes offers a glimpse into the yet unknown world of quantum gravity.
It is natural to generalize pp-waves to higher dimensions, where they enjoy similar properties to those we have discussed. C. M. Hull has shown that such
higher dimensional pp-waves are essential building blocks for eleven-dimensional supergravity
Supergravity
In theoretical physics, supergravity is a field theory that combines the principles of supersymmetry and general relativity. Together, these imply that, in supergravity, the supersymmetry is a local symmetry...
.
Geometric and physical properties
PP-waves enjoy numerous striking properties. Some of their more abstract mathematical properties have already been mentioned. In this section we can discuss only a few additional properties.Consider an inertial observer in Minkowski spacetime who encounters a sandwich plane wave. Such an observer will experience some interesting optical effects. If he looks into the oncoming wavefronts at distant galaxies which have already encountered the wave, he will see their images undistorted. This must be the case, since he cannot know the wave is coming until it reaches his location, for it is traveling at the speed of light. However, this can be confirmed by direct computation of the optical scalars of the null congruence
. Now suppose that after the wave passes, our observer turns about face and looks through the departing wavefronts at distant galaxies which the wave has not yet reached. Now he sees their optical images sheared and magnified (or demagnified) in a time-dependent manner. If the wave happens to be a polarized gravitational plane wave, he will see circular images alternately squeezed horizontally while expanded vertically, and squeezed vertically while expanded horizontally. This directly exhibits the characteristic effect of a gravitational wave in general relativity on light.The effect of a passing polarized gravitational plane wave on the relative positions of a cloud of (initially static) test particles will be qualitatively very similar. We might mention here that in general, the motion of test particles in pp-wave spacetimes can exhibit chaos
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
.
The fact that Einstein's field equation is nonlinear is well-known. This implies that if you have two exact solutions, there is almost never any way to linearly superimpose
Superposition principle
In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
them. PP waves provide a rare exception to this rule:
if you have two PP waves sharing the same covariantly constant null vector (the same geodesic null congruence, i.e. the same wave vector field), with metric functions
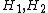respectively, then 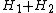gives a third exact solution.Roger Penrose
Roger Penrose
Sir Roger Penrose OM FRS is an English mathematical physicist and Emeritus Rouse Ball Professor of Mathematics at the Mathematical Institute, University of Oxford and Emeritus Fellow of Wadham College...
has observed that near a null geodesic, every Lorentzian spacetime looks like a plane wave. To show this, he used techniques imported from algebraic geometry to "blow up" the spacetime so that the given null geodesic becomes the covariantly constant null geodesic congruence of a plane wave. This construction is called a Penrose limit.
Penrose also pointed out that in a pp-wave spacetime, all the polynomial scalar invariants of the Riemann tensor
Riemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
vanish identically, yet the curvature is almost never zero. This is because in four-dimension all pp-waves belong to the class of VSI spacetime
VSI spacetime
In mathematical physics, VSI spacetimes are Lorentzian manifolds with all polynomial curvature invariants of all orders vanishing. An example with this property in four dimensions is a pp-wave. VSI spacetimes however also contain some other four-dimensional Kundt spacetimes of Petrov type N and III...
s. Such statement does not hold in higher-dimensions since there are higher-dimensional pp-waves of algebraic type II with non-vanishing polynomial scalar invariants. If you view the Riemann tensor as a second rank tensor acting on bivectors, the vanishing of invariants is analogous to the fact that a nonzero null vector has vanishing squared length.
Penrose was also the first to understand the strange nature of causality in
pp-sandwich wave spacetimes. He showed that some or all of the null geodesics emitted at a given event will be refocused at a later event (or string of events). The details depend upon whether the wave is purely gravitational, purely electromagnetic, or neither.
Every pp-wave admits many different Brinkmann charts. These are related by coordinate transformations, which in this context may be considered to be gauge transformations. In the case of plane waves, these gauge transformations allow us to always regard two colliding plane waves to have parallel wavefronts,
and thus the waves can be said to collide head-on.
This is an exact result in fully nonlinear general relativity which is analogous to a similar result concerning electromagnetic plane wave
Plane wave
In the physics of wave propagation, a plane wave is a constant-frequency wave whose wavefronts are infinite parallel planes of constant peak-to-peak amplitude normal to the phase velocity vector....
s as treated in special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
.
Examples
There are many noteworthy explicit examples of pp-waves.("Explicit" means that the metric functions can be written down in terms of elementary functions
or perhaps well-known special functions
Special functions
Special functions are particular mathematical functions which have more or less established names and notations due to their importance in mathematical analysis, functional analysis, physics, or other applications....
such as Mathieu function
Mathieu function
In mathematics, the Mathieu functions are certain special functions useful for treating a variety of problems in applied mathematics, including*vibrating elliptical drumheads,*quadrupoles mass filters and quadrupole ion traps for mass spectrometry...
s.)
Explicit examples of axisymmetric pp-waves include
- The Aichelburg-Sexl ultraboostAichelburg-Sexl ultraboostIn general relativity, the Aichelburg–Sexl ultraboost is an exact solution which models the physical experience of an observer moving past a spherically symmetric gravitating object at nearly the speed of light. It was introduced by Peter C. Aichelburg and Roman U...
is an impulsive plane wave which models the physical experience of an observer who whizzes by a spherically symmetric gravitating objectSchwarzschild metricIn Einstein's theory of general relativity, the Schwarzschild solution describes the gravitational field outside a spherical, uncharged, non-rotating mass such as a star, planet, or black hole. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth or...
at nearly the speed of light,
- The Bonnor beamBonnor beamIn general relativity, the Bonnor beam is an exact solution which models an infinitely long, straight beam of light. It is an explicit example of a pp-wave spacetime. It is named after William B...
is an axisymmetric plane wave which models the gravitational field of an infinitely long beam of incoherent electromagnetic radiation.
Explicit examples of plane wave spacetimes include
- exact monochromatic gravitational plane wave and monochromatic electromagnetic plane waveMonochromatic electromagnetic plane waveIn general relativity, the monochromatic electromagnetic plane wave spacetime is the analog of the monochromatic plane waves known from Maxwell's theory...
solutions, which generalize solutions which are well-known from weak-field approximation,
- the Schwarzschild generating plane wave, a gravitational plane wave which, should it collide head-on with a twin, will produce in the interaction zone of the resulting colliding plane wave solution a region which is locally isometric to part of the interior of a Schwarzschild black holeSchwarzschild metricIn Einstein's theory of general relativity, the Schwarzschild solution describes the gravitational field outside a spherical, uncharged, non-rotating mass such as a star, planet, or black hole. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth or...
, thereby permitting a classical peek at the local geometry inside the event horizonEvent horizonIn general relativity, an event horizon is a boundary in spacetime beyond which events cannot affect an outside observer. In layman's terms it is defined as "the point of no return" i.e. the point at which the gravitational pull becomes so great as to make escape impossible. The most common case...
,
- the uniform electromagnetic plane wave; this spacetime is foliated by spacelike hyperslices which are isometric to
,
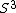- the wave of death is a gravitational plane wave exhibiting a strong nonscalar null curvature singularity, which propagates through an initially flat spacetime, progressively destroying the universe,
- homogeneous plane waves, or SG11 plane waves (type 11 in the Sippel and Gönner symmetry classification), which exhibit a weak nonscalar null curvature singularity and which arise as the Penrose limits of an appropriate null geodesic approaching the curvature singularity which is present in many physically important solutions, including the Schwarzschild black holesSchwarzschild metricIn Einstein's theory of general relativity, the Schwarzschild solution describes the gravitational field outside a spherical, uncharged, non-rotating mass such as a star, planet, or black hole. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth or...
and FRW cosmological models.