Poisson-Lie group
Encyclopedia
In mathematics
, a Poisson–Lie group is a Poisson manifold
that is also a Lie group
, with the group multiplication being compatible with the Poisson algebra
structure on the manifold. The algebra of a Poisson–Lie group is a Lie bialgebra
.
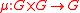with 
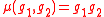is a Poisson map, where the manifold G×G has been given the structure of a product Poisson manifold.
Explicitly, the following identity must hold for a Poisson–Lie group:
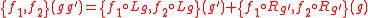
where f1 and f2 are real-valued, smooth functions on the Lie group, while g and g' are elements of the Lie group. Here, Lg denotes left-multiplication and Rg denotes right-multiplication.
If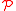
denotes the corresponding Poisson bivector on G, the condition above can be equivalently stated as
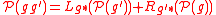
Note that for Poisson-Lie group always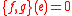
, or equivalently 
. This means that non-trivial Poisson-Lie structure is never symplectic, not even of constant rank.
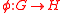is defined to be both a Lie group homomorphism and a Poisson map. Although this is the "obvious" definition, neither left translations nor right translations are Poisson maps. Also, the inversion map 
taking 
is not a Poisson map either, although it is an anti-Poisson map:
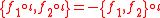
for any two smooth functions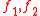
on G.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Poisson–Lie group is a Poisson manifold
Poisson manifold
In mathematics, a Poisson manifold is a differentiable manifold M such that the algebra C^\infty\, of smooth functions over M is equipped with a bilinear map called the Poisson bracket, turning it into a Poisson algebra...
that is also a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
, with the group multiplication being compatible with the Poisson algebra
Poisson algebra
In mathematics, a Poisson algebra is an associative algebra together with a Lie bracket that also satisfies Leibniz' law; that is, the bracket is also a derivation. Poisson algebras appear naturally in Hamiltonian mechanics, and are also central in the study of quantum groups...
structure on the manifold. The algebra of a Poisson–Lie group is a Lie bialgebra
Lie bialgebra
In mathematics, a Lie bialgebra is the Lie-theoretic case of a bialgebra: its a set with a Lie algebra and a Lie coalgebra structure which are compatible....
.
Definition
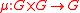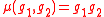A Poisson–Lie group is a Lie group G equipped with a Poisson bracket for which the group multiplication with is a Poisson map, where the manifold G×G has been given the structure of a product Poisson manifold.Explicitly, the following identity must hold for a Poisson–Lie group:
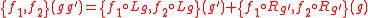
where f1 and f2 are real-valued, smooth functions on the Lie group, while g and g' are elements of the Lie group. Here, Lg denotes left-multiplication and Rg denotes right-multiplication.
If
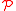denotes the corresponding Poisson bivector on G, the condition above can be equivalently stated as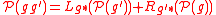Note that for Poisson-Lie group always
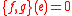, or equivalently . This means that non-trivial Poisson-Lie structure is never symplectic, not even of constant rank.Homomorphisms
A Poisson–Lie group homomorphism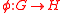 is defined to be both a Lie group homomorphism and a Poisson map. Although this is the "obvious" definition, neither left translations nor right translations are Poisson maps. Also, the inversion map taking is not a Poisson map either, although it is an anti-Poisson map: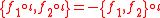for any two smooth functions
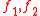on G.