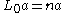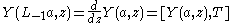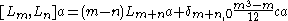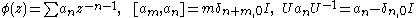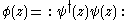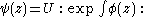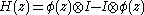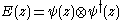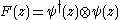Vertex operator algebra
Encyclopedia
In mathematics
, a vertex operator algebra (VOA) is an algebraic structure that plays an important role in conformal field theory
and related areas of physics. Vertex operator algebras have proven useful in purely mathematical contexts such as monstrous moonshine
and the geometric Langlands correspondence.
Vertex operator algebras were first introduced by Richard Borcherds
in 1986, motivated by the vertex operators arising from field insertions in two dimensional conformal field theory, a framework that is essential to define string theory
. The axioms of a vertex operator algebra are a formal algebraic interpretation of what physicists called chiral algebra
s, whose definition was made mathematically rigorous by Alexander Beilinson
and Vladimir Drinfel'd
.
Important examples of vertex operator algebras include lattice VOAs (modeling lattice conformal field theories), VOAs given by representations of affine Kac-Moody algebras (from the WZW model
), the Virasoro VOAs (i.e., VOAs corresponding to representations of the Virasoro algebra
) and the moonshine module V♮, constructed by Frenkel
, Lepowsky
and Meurman
in 1988.
V, together with an identity element 1∈V, an endomorphism
T: V → V, and a linear multiplication map
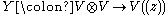
from the tensor product
of V with itself to the space V((z)) of all formal Laurent series with coefficients in V, written as:
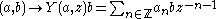
and satisfying the following axioms:
The multiplication map is often written as a state-field correspondence
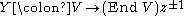
associating an operator-valued formal distribution (called a vertex operator) to each vector. Physically, the correspondence is an insertion at the origin, and T is a generator of infinitesimal translations. The four-point axiom combines associativity and commutativity, up to singularities. Note that the translation axiom implies Ta = a-21, so T is determined by Y.
A vertex algebra V is Z+-graded if

such that if a ∈ Vk and b ∈ Vm, then an b ∈ Vk+m-n-1.
A vertex operator algebra is a Z+-graded vertex algebra equipped with a Virasoro element ω ∈ V2, such that the vertex operator
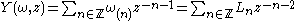
satisfies for any a ∈ Vn, the relations:
where c is a constant called the central charge, or rank of V. In particular, this gives V the structure of a representation of the Virasoro algebra.
of operators in a 2D Euclidean chiral conformal field theory. The two dimensional Euclidean space is treated as a Riemann sphere
with the point at infinity removed. V is taken to be the space of all operators at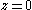 . The operator product expansion is holomorphic in z and so, we can make a Laurent expansion of it. 1 is the identity operator. We treat an operator valued holomorphic map over
. The operator product expansion is holomorphic in z and so, we can make a Laurent expansion of it. 1 is the identity operator. We treat an operator valued holomorphic map over 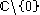 as a formal Laurent series. This is denoted by the notation V((z)). A holomorphic map over
as a formal Laurent series. This is denoted by the notation V((z)). A holomorphic map over  is given by a Taylor series
is given by a Taylor series
and as a formal power series
, this is denoted byVz
.
The operator b(0) is abstracted to b and the operator a(z) to Y(a,z). The derivative a'(z) is abstracted to -Ta.
If one considers only the singular part of the OPE in a Vertex algebra, one arrives at the definition of a Lie conformal algebra
. Since one is often only concerned with the singular part of the OPE, this makes Lie conformal algebras a natural object to study.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a vertex operator algebra (VOA) is an algebraic structure that plays an important role in conformal field theory
Conformal field theory
A conformal field theory is a quantum field theory that is invariant under conformal transformations...
and related areas of physics. Vertex operator algebras have proven useful in purely mathematical contexts such as monstrous moonshine
Monstrous moonshine
In mathematics, monstrous moonshine, or moonshine theory, is a term devised by John Horton Conway and Simon P. Norton in 1979, used to describe the connection between the monster group M and modular functions .- History :Specifically, Conway and Norton, following an initial observationby John...
and the geometric Langlands correspondence.
Vertex operator algebras were first introduced by Richard Borcherds
Richard Borcherds
Richard Ewen Borcherds is a British mathematician specializing in lattices, number theory, group theory, and infinite-dimensional algebras. He was awarded the Fields Medal in 1998.- Personal life :...
in 1986, motivated by the vertex operators arising from field insertions in two dimensional conformal field theory, a framework that is essential to define string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
. The axioms of a vertex operator algebra are a formal algebraic interpretation of what physicists called chiral algebra
Chiral algebra
In mathematics, a chiral algebra is an algebraic structure introduced by as a rigorous version of the rather vague concept of a chiral algebra in physics....
s, whose definition was made mathematically rigorous by Alexander Beilinson
Alexander Beilinson
Alexander A. Beilinson is the David and Mary Winton Green University Professor at the University of Chicago and works on mathematics. His research has spanned representation theory, algebraic geometry and mathematical physics...
and Vladimir Drinfel'd
Vladimir Drinfel'd
Vladimir Gershonovich Drinfel'd is a Ukrainian and Soviet mathematician at the University of Chicago.The work of Drinfeld related algebraic geometry over finite fields with number theory, especially the theory of automorphic forms, through the notions of elliptic module and the theory of the...
.
Important examples of vertex operator algebras include lattice VOAs (modeling lattice conformal field theories), VOAs given by representations of affine Kac-Moody algebras (from the WZW model
Wess-Zumino-Witten model
In theoretical physics and mathematics, the Wess–Zumino–Witten model, also called the Wess–Zumino–Novikov–Witten model, is a simple model of conformal field theory whose solutions are realized by affine Kac–Moody algebras...
), the Virasoro VOAs (i.e., VOAs corresponding to representations of the Virasoro algebra
Virasoro algebra
In mathematics, the Virasoro algebra is a complex Lie algebra, given as a central extension of the complex polynomial vector fields on the circle, and is widely used in conformal field theory and string theory....
) and the moonshine module V♮, constructed by Frenkel
Igor Frenkel
Igor Borisovich Frenkel is a mathematician at Yale University working in representation theory and mathematical physics.-Biography:...
, Lepowsky
James Lepowsky
James Lepowsky is a professor of mathematics at Rutgers University, New Jersey. Previously he taught at Yale University. He received his Ph.D from M.I.T. in 1970 where his advisor was Bertram Kostant. Lepowsky graduated from Stuyvesant High School in 1961, 16 years after Kostant...
and Meurman
Arne Meurman
Arne Meurman is a Swedish mathematician working on finite groups and vertex operator algebras. Currently he is a professor at Lund University....
in 1988.
Formal definition
A vertex algebra is a vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V, together with an identity element 1∈V, an endomorphism
Endomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
T: V → V, and a linear multiplication map
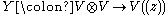
from the tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of V with itself to the space V((z)) of all formal Laurent series with coefficients in V, written as:
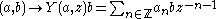
and satisfying the following axioms:
- (Identity) For any a ∈ V,
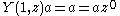 and
and 
- (Translation) T(1) = 0, and for any a, b ∈ V,

- (Four point function) For any a, b, c ∈ V, there is an element

such that Y(a,z)Y(b,w)c, Y(b,w)Y(a,z)c, and Y(Y(a,z-w)b,w)c are the expansions of X(a,b,c;z,w) in V((z))((w)), V((w))((z)), and V((w))((z-w)), respectively.
The multiplication map is often written as a state-field correspondence
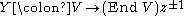
associating an operator-valued formal distribution (called a vertex operator) to each vector. Physically, the correspondence is an insertion at the origin, and T is a generator of infinitesimal translations. The four-point axiom combines associativity and commutativity, up to singularities. Note that the translation axiom implies Ta = a-21, so T is determined by Y.
A vertex algebra V is Z+-graded if

such that if a ∈ Vk and b ∈ Vm, then an b ∈ Vk+m-n-1.
A vertex operator algebra is a Z+-graded vertex algebra equipped with a Virasoro element ω ∈ V2, such that the vertex operator
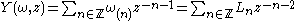
satisfies for any a ∈ Vn, the relations:
where c is a constant called the central charge, or rank of V. In particular, this gives V the structure of a representation of the Virasoro algebra.
Motivation and related algebraic structures
The axioms of a vertex algebra are obtained from abstracting away the essentials of the operator product expansionOperator product expansion
- 2D Euclidean quantum field theory :In quantum field theory, the operator product expansion is a Laurent series expansion of two operators...
of operators in a 2D Euclidean chiral conformal field theory. The two dimensional Euclidean space is treated as a Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
with the point at infinity removed. V is taken to be the space of all operators at
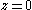 . The operator product expansion is holomorphic in z and so, we can make a Laurent expansion of it. 1 is the identity operator. We treat an operator valued holomorphic map over
. The operator product expansion is holomorphic in z and so, we can make a Laurent expansion of it. 1 is the identity operator. We treat an operator valued holomorphic map over  as a formal Laurent series. This is denoted by the notation V((z)). A holomorphic map over
as a formal Laurent series. This is denoted by the notation V((z)). A holomorphic map over  is given by a Taylor series
is given by a Taylor seriesTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
and as a formal power series
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
, this is denoted by
Z
Z is the twenty-sixth and final letter of the basic modern Latin alphabet.-Name and pronunciation:In most dialects of English, the letter's name is zed , reflecting its derivation from the Greek zeta but in American English, its name is zee , deriving from a late 17th century English dialectal...
The operator b(0) is abstracted to b and the operator a(z) to Y(a,z). The derivative a'(z) is abstracted to -Ta.
If one considers only the singular part of the OPE in a Vertex algebra, one arrives at the definition of a Lie conformal algebra
Lie conformal algebra
A Lie conformal algebra is in some sense a generalization of a Lie algebra in the sense that it too is a "Lie algebra," though a in different pseudo-tensor category...
. Since one is often only concerned with the singular part of the OPE, this makes Lie conformal algebras a natural object to study.
Alternative definitions
Another way to think of vertex algebras is as a generalisation of a Lie algebra with the addition of a continuous variable to both the generators of the algebra and the structure constant. (The structure constants define the algebra). So we would have:-
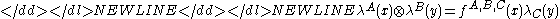
which can also be expressed without the y dependence as:
-
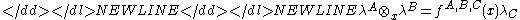
which reveals the Vertex Multiplication as a group operation in which the group constants vary with their position on the conformal sheet.
Jacobi identity
The vertex algebras satisfy the Jacobi identity given by:
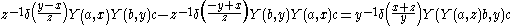
which can also be written as
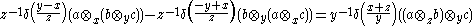
where the delta function is defined formally by:
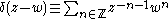
(always expanded in terms of the second variable w)
A trivial example
To make things more concrete a trivial example of a commutative vertex algebra is presented. We take the vector space V to consist of 2-vectors, v, with components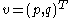 . If we think of this vector as a complex number, p+qi, the Y function can be seen as taking it from its vector form to a 2x2 matrix form of (p-qz)+qi. The p and q are real numbers.
. If we think of this vector as a complex number, p+qi, the Y function can be seen as taking it from its vector form to a 2x2 matrix form of (p-qz)+qi. The p and q are real numbers.

So that multiplication between two vectors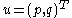 and
and  is defined by:
is defined by:
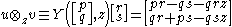
The identity element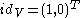 so that:
so that:
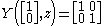
and

and the operator T in this example is:
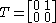
it is easy to check:
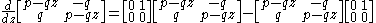
Since the Y matrices commute, locality is satisfied trivially. Non-trivial vertex algebras and vertex operator algebras would require infinite sized matrices to represent them. All the terms with powers of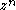 with n<0 must be zero when applied to the identity vector
with n<0 must be zero when applied to the identity vector 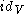 . i.e. of the form:
. i.e. of the form:
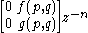
but adding a single term like this won't commute with the other terms. Hence our example would no longer be trivial since we may need an infinite number of terms to restore locality.
Heisenberg Lie algebra example
The Heisenberg Lie algebra is defined by the commutation relations: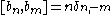
One representation is to define the operators b, in terms of the dummy variables x as:
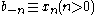

and .
.
This can be made into a vertex algebra by the definition: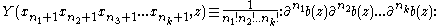
where :..: denotes normal ordering (i.e. moving all derivatives in x to the right). Thus Y(1,z) = Id.
T is defined by the conditions T.1 = 0 and

Setting

it follows that
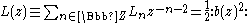
and hence:
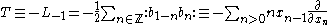
Virasoro vertex operator algebra example
The Virasoro vertex operator algebra is a conformal vertex algebra. It is defined as follows:

With L(z) defined as above. So we have and with
and with  and
and 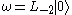 . We see that this satisfies the axioms of a vertex algebra and includes a representation of the Virasoro algebra. The fact that the Virasoro field
. We see that this satisfies the axioms of a vertex algebra and includes a representation of the Virasoro algebra. The fact that the Virasoro field 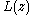 is local can be deduced from the formula for its self-commutator:
is local can be deduced from the formula for its self-commutator:
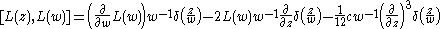
where c is central charge.
Monster Vertex Algebra
The monster vertex algebraMonster vertex algebraThe monster vertex algebra is a vertex algebra acted on by the monster group that was constructed by Igor Frenkel, James Lepowsky, and Arne Meurman. R...
is a conformal vertex operator derived from 26 dimensional bosonic string theory compactified on the hyper-torus induced by the Leech latticeLeech latticeIn mathematics, the Leech lattice is an even unimodular lattice Λ24 in 24-dimensional Euclidean space E24 found by .-History:Many of the cross-sections of the Leech lattice, including the Coxeter–Todd lattice and Barnes–Wall lattice, in 12 and 16 dimensions, were found much earlier than...
and orbifolded by the two-element reflection group. It is denoted as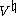 . It was used to prove the Monstrous moonshineMonstrous moonshineIn mathematics, monstrous moonshine, or moonshine theory, is a term devised by John Horton Conway and Simon P. Norton in 1979, used to describe the connection between the monster group M and modular functions .- History :Specifically, Conway and Norton, following an initial observationby John...
. It was used to prove the Monstrous moonshineMonstrous moonshineIn mathematics, monstrous moonshine, or moonshine theory, is a term devised by John Horton Conway and Simon P. Norton in 1979, used to describe the connection between the monster group M and modular functions .- History :Specifically, Conway and Norton, following an initial observationby John...
conjectures.
In the string model the vectors a in Y(a,z) are the different states or vibrational modes of the string which correspond to different particles and polarisations and z is a point (or vertex) on the world sheet which corresponds to an ingoing or outgoing string. Hence why it is called a Vertex Algebra.
Vertex operator superalgebra
When the underlying vector space V has a Z2 grading, so that it splits as a sum of even and odd parts
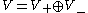
with 1 in V+, the structure of a vertex superalgebra can be defined on V by incorporating the usual rule of signs
in the axiom for the four point function:
- (Four point function) For any a, b, c ∈ V±, there is an element
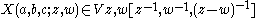
such that Y(a,z)Y(b,w)c, εY(b,w)Y(a,z)c, and Y(Y(a,z-w)b,w)c are the expansions of X(a,b,c;z,w) in V((z))((w)), V((w))((z)), and V((w))((z-w)), respectively, where ε is -1 if both a and b are odd and 1 otherwise.
If in addition there is a Virasoro element ω in the even part of V2, then V is called a vertex operator superalgebra.
One of the simplest examples is the vertex operator superalgebra generated by a single complex fermion.
Vertex operator algebra defined by a lattice
Let Λ be an integral lattice in Euclidean space X = RN, i.e. a subgroup isomorphic to Zn with m ≤ N and such that (α,β) lies in Z for α,β in Λ . The lattice is said to be even if (α,α) is even for each α in Λ. Setting

there is an essentially unique normalised cocycle ε(α,β) with values ±1 such that
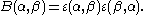
and the cocycle identity
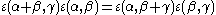
is satisfied along with the normalisation conditions

A cocycle representation can be defined on C[Λ], with basis eα (α in Λ), by

Thus
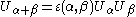
and
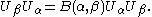
The operators Uα are unitary if the eα are taken to be orthonormal.
There is a bosonic system associated to X, namely operators vn depending linearly on v in X such that

In addition the system has a derivation D satisfying with
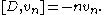
There is a unique irreducible representation of this system characterised by the existence of a vacuum vector Ω with vn Ω = 0 for n ≥ 0. The underlying space S has a unique inner product structure for which vn* = v–n.
The vector space V of the vertex superalgebra is defined by
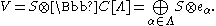
The operators vn with n non-zero act on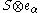 exactly as they act on S,
exactly as they act on S,

The operators v0 act as scalars on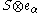 :
:

For each v in X define the field

For each α in Λ define

where
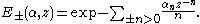
If v(i) is an orthonormal basis of X, define
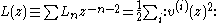
where the normal ordering is given by

Then the vertex operators v(z) and Φα(z) generate a vertex operator superalgebra with underlying space
V. The operators D and T are given by L0 and L–1 respectively.
Examples
- The lattice Z in R gives the vertex operator superalgebra corresponding to a single complex fermion. This is another way of phrasing the celebrated fermion-boson correspondence. The fermion field ψ(z) and its conjugate field ψ†(z) are defined by
-
- The correspondence between fermions and a single charged boson field
- takes the form
- where the normal ordered exponential is interpreted as a vertex operator of the type constructed above.
- The lattice √2 Z in R gives the vertex operator algebra corresponding to the affine Kac-Moody algebra
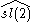 at level one. It is realised by the fields
at level one. It is realised by the fields
- If Λ is even, is generated by its "root vectors" (those satisfying (α,α)=2), spans X, and any two root vectors are joined by a chain of root vectors with consecutive inner products non-zero then the vertex operator algebra corresponds to the affine Kac-Moody algebra of a simply laced simple Lie algebra at level one. The zero modes of the v(z)'s and the Φα(z)'s corresponding to root vectors give a construction of the underlying simple Lie algebra, related to a presentation originally due to Jacques TitsJacques TitsJacques Tits is a Belgian and French mathematician who works on group theory and geometry and who introduced Tits buildings, the Tits alternative, and the Tits group.- Career :Tits received his doctorate in mathematics at the age of 20...
. The definition of the vertex operators Φα(z) in this context is originally due to Victor KacVictor KacVictor G. Kac is a Soviet and American mathematician at MIT, known for his work in representation theory. He discovered Kac–Moody algebras, and used the Weyl–Kac character formula for them to reprove the Macdonald identities...
, Igor FrenkelIgor FrenkelIgor Borisovich Frenkel is a mathematician at Yale University working in representation theory and mathematical physics.-Biography:...
and independently Graeme SegalGraeme SegalGraeme Bryce Segal is a British mathematician, and professor at the University of Oxford.Segal was educated at the University of Sydney, where he received his BSc degree in 1961. He went on to receive his D.Phil...
. It is based on the earlier construction by Sergio FubiniSergio FubiniSergio Fubini was an Italian theoretical physicist. He was one of the pioneers of string theory. Politically he engaged himself actively for peace in the Middle East.- Biography :...
and Gabriele VenezianoGabriele VenezianoGabriele Veneziano, born in Florence, Italy), is an Italian theoretical physicist and the founder of string theory. . Has spent most of his scientific activities at CERN in Geneva, Switzerland...
of the tachyonic vertex operatorTachyonA tachyon is a hypothetical subatomic particle that always moves faster than light. In the language of special relativity, a tachyon would be a particle with space-like four-momentum and imaginary proper time. A tachyon would be constrained to the space-like portion of the energy-momentum graph...
in the dual resonance modelDual resonance modelIn theoretical physics, a dual resonance model arose the early investigation of string theory as an S-matrix theory of the strong interaction....
.
- (Four point function) For any a, b, c ∈ V±, there is an element
-