Substitution tiling
Encyclopedia
In geometry, a tile substitution is a useful method for constructing highly ordered tiling
s. Most importantly, some tile substitutions generate aperiodic tiling
s, which are tilings whose prototiles do not admit any tiling with translational symmetry
. The most famous of these are the Penrose tiling
s.
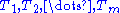 , an expanding map
, an expanding map  and a dissection rule showing how to dissect the expanded prototiles
and a dissection rule showing how to dissect the expanded prototiles  to form copies of some prototiles
to form copies of some prototiles 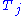 . Intuitively, higher and higher iterations of tile substitution produce a tiling of the plane called a substitution tiling. Some substitution tilings are periodic
. Intuitively, higher and higher iterations of tile substitution produce a tiling of the plane called a substitution tiling. Some substitution tilings are periodic
, defined as having translational symmetry
. Among the nonperiodic substitution tilings are some aperiodic tiling
s, those whose prototiles cannot be rearranged to form a periodic tiling (usually if one requires in addition some matching rules).
A simple example that produces a periodic tiling has only one prototile, namely a square:
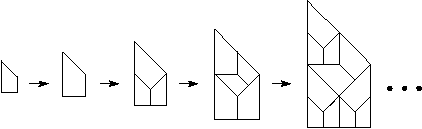
By iterating this tile substitution, larger and larger regions of the plane are covered with a square grid. A more sophisticated example with two prototiles is shown below, with the two steps of blowing up and dissecting are merged into one step in the figure.
One may intuitively get an idea how this procedure yields a substitution tiling of the entire plane
. A mathematically proper definition is given below. Substitution tilings are notably useful as ways of defining aperiodic tiling
s, which are objects of interest in many fields of mathematics
, including automata theory
, combinatorics
, discrete geometry
, dynamical systems, group theory
, harmonic analysis
and number theory
, not to mention the impact which were induced by those tilings in crystallography
and chemistry
. In particular, the celebrated Penrose tiling
is an example of an aperiodic substitution tiling.
discovered a family of aperiodic tilings, now called Penrose tiling
s. The first description was given in terms of 'matching rules' treating the prototiles as jigsaw puzzle
pieces. The proof that copies of these prototiles can be put together to form a tiling
of the plane, but cannot do so periodically, uses a construction that can be cast as a substitution tiling of the prototiles. In 1977 Robert Ammann
discovered a number of sets of aperiodic prototiles, i.e., prototiles with matching rules forcing nonperiodic tilings; in particular, he rediscovered Penrose's first example. This work gave an impact to scientists working in crystallography
, eventually leading to the discovery of quasicrystals. In turn, the interest in quasicrystals led to the discovery of several well-ordered aperiodic tilings. Many of them can be easily described as substitution tilings.
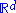 that are well-behaved
that are well-behaved
, in the sense that a region is a nonempty compact subset that is the closure
of its interior
.
We take a set of regions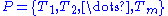 as prototiles. A placement of a prototile
as prototiles. A placement of a prototile 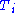 is a pair
is a pair 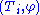 where
where 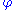 is an isometry
is an isometry
of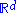 . The image
. The image 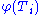 is called the placement's region. A tiling T is a set of prototile placements whose regions have pairwise disjoint interiors. We say that the tiling T is a tiling of W where W is the union of the regions of the placements in T.
is called the placement's region. A tiling T is a set of prototile placements whose regions have pairwise disjoint interiors. We say that the tiling T is a tiling of W where W is the union of the regions of the placements in T.
A tile substitution is often loosely defined in the literature. A precise definition is as follows.
A tile substitution with respect to the prototiles P is a pair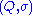 , where
, where 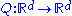 is a linear map, all of whose eigenvalues are larger than one in modulus, together with a substitution rule
is a linear map, all of whose eigenvalues are larger than one in modulus, together with a substitution rule  that maps each
that maps each 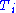 to a tiling of
to a tiling of 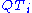 . The tile substitution
. The tile substitution  induces a map from any tiling T of a region W to a tiling
induces a map from any tiling T of a region W to a tiling 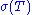 of
of  , defined by
, defined by
Note, that the prototiles can be deduced from the tile substitution. Therefore it is not necessary to include them in the tile substitution .
.
Every tiling of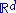 , where any finite part of it is congruent to a subset
, where any finite part of it is congruent to a subset
of some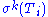 is called a substitution tiling (for the tile substitution
is called a substitution tiling (for the tile substitution 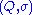 ).
).
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
s. Most importantly, some tile substitutions generate aperiodic tiling
Aperiodic tiling
An aperiodic tiling is a tiling obtained from an aperiodic set of tiles. Properly speaking, aperiodicity is a property of particular sets of tiles; any given finite tiling is either periodic or non-periodic...
s, which are tilings whose prototiles do not admit any tiling with translational symmetry
Translational symmetry
In geometry, a translation "slides" an object by a a: Ta = p + a.In physics and mathematics, continuous translational symmetry is the invariance of a system of equations under any translation...
. The most famous of these are the Penrose tiling
Penrose tiling
A Penrose tiling is a non-periodic tiling generated by an aperiodic set of prototiles named after Sir Roger Penrose, who investigated these sets in the 1970s. The aperiodicity of the Penrose prototiles implies that a shifted copy of a Penrose tiling will never match the original...
s.
Introduction
A tile substitution is described by a set of prototiles (tile shapes)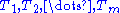 , an expanding map
, an expanding map  and a dissection rule showing how to dissect the expanded prototiles
and a dissection rule showing how to dissect the expanded prototiles 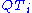 to form copies of some prototiles
to form copies of some prototiles 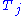 . Intuitively, higher and higher iterations of tile substitution produce a tiling of the plane called a substitution tiling. Some substitution tilings are periodic
. Intuitively, higher and higher iterations of tile substitution produce a tiling of the plane called a substitution tiling. Some substitution tilings are periodicPeriodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
, defined as having translational symmetry
Translational symmetry
In geometry, a translation "slides" an object by a a: Ta = p + a.In physics and mathematics, continuous translational symmetry is the invariance of a system of equations under any translation...
. Among the nonperiodic substitution tilings are some aperiodic tiling
Aperiodic tiling
An aperiodic tiling is a tiling obtained from an aperiodic set of tiles. Properly speaking, aperiodicity is a property of particular sets of tiles; any given finite tiling is either periodic or non-periodic...
s, those whose prototiles cannot be rearranged to form a periodic tiling (usually if one requires in addition some matching rules).
A simple example that produces a periodic tiling has only one prototile, namely a square:
By iterating this tile substitution, larger and larger regions of the plane are covered with a square grid. A more sophisticated example with two prototiles is shown below, with the two steps of blowing up and dissecting are merged into one step in the figure.
One may intuitively get an idea how this procedure yields a substitution tiling of the entire plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
. A mathematically proper definition is given below. Substitution tilings are notably useful as ways of defining aperiodic tiling
Aperiodic tiling
An aperiodic tiling is a tiling obtained from an aperiodic set of tiles. Properly speaking, aperiodicity is a property of particular sets of tiles; any given finite tiling is either periodic or non-periodic...
s, which are objects of interest in many fields of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, including automata theory
Automata theory
In theoretical computer science, automata theory is the study of abstract machines and the computational problems that can be solved using these machines. These abstract machines are called automata...
, combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, discrete geometry
Discrete geometry
Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles,...
, dynamical systems, group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, harmonic analysis
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
and number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, not to mention the impact which were induced by those tilings in crystallography
Crystallography
Crystallography is the experimental science of the arrangement of atoms in solids. The word "crystallography" derives from the Greek words crystallon = cold drop / frozen drop, with its meaning extending to all solids with some degree of transparency, and grapho = write.Before the development of...
and chemistry
Chemistry
Chemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds....
. In particular, the celebrated Penrose tiling
Penrose tiling
A Penrose tiling is a non-periodic tiling generated by an aperiodic set of prototiles named after Sir Roger Penrose, who investigated these sets in the 1970s. The aperiodicity of the Penrose prototiles implies that a shifted copy of a Penrose tiling will never match the original...
is an example of an aperiodic substitution tiling.
History
In 1973 and 1974, Roger PenroseRoger Penrose
Sir Roger Penrose OM FRS is an English mathematical physicist and Emeritus Rouse Ball Professor of Mathematics at the Mathematical Institute, University of Oxford and Emeritus Fellow of Wadham College...
discovered a family of aperiodic tilings, now called Penrose tiling
Penrose tiling
A Penrose tiling is a non-periodic tiling generated by an aperiodic set of prototiles named after Sir Roger Penrose, who investigated these sets in the 1970s. The aperiodicity of the Penrose prototiles implies that a shifted copy of a Penrose tiling will never match the original...
s. The first description was given in terms of 'matching rules' treating the prototiles as jigsaw puzzle
Jigsaw puzzle
A jigsaw puzzle is a tiling puzzle that requires the assembly of numerous small, often oddly shaped, interlocking and tessellating pieces.Each piece usually has a small part of a picture on it; when complete, a jigsaw puzzle produces a complete picture...
pieces. The proof that copies of these prototiles can be put together to form a tiling
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
of the plane, but cannot do so periodically, uses a construction that can be cast as a substitution tiling of the prototiles. In 1977 Robert Ammann
Robert Ammann
Robert Ammann was an amateur mathematician who made several significant and groundbreaking contributions to the theory of quasicrystals and aperiodic tilings....
discovered a number of sets of aperiodic prototiles, i.e., prototiles with matching rules forcing nonperiodic tilings; in particular, he rediscovered Penrose's first example. This work gave an impact to scientists working in crystallography
Crystallography
Crystallography is the experimental science of the arrangement of atoms in solids. The word "crystallography" derives from the Greek words crystallon = cold drop / frozen drop, with its meaning extending to all solids with some degree of transparency, and grapho = write.Before the development of...
, eventually leading to the discovery of quasicrystals. In turn, the interest in quasicrystals led to the discovery of several well-ordered aperiodic tilings. Many of them can be easily described as substitution tilings.
Mathematical definition
We will consider regions in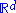 that are well-behaved
that are well-behavedWell-behaved
Mathematicians very frequently speak of whether a mathematical object — a function, a set, a space of one sort or another — is "well-behaved" or not. The term has no fixed formal definition, and is dependent on mathematical interests, fashion, and taste...
, in the sense that a region is a nonempty compact subset that is the closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of its interior
Interior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
.
We take a set of regions
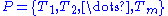 as prototiles. A placement of a prototile
as prototiles. A placement of a prototile 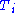 is a pair
is a pair 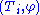 where
where 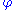 is an isometry
is an isometryIsometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
of
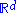 . The image
. The image 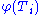 is called the placement's region. A tiling T is a set of prototile placements whose regions have pairwise disjoint interiors. We say that the tiling T is a tiling of W where W is the union of the regions of the placements in T.
is called the placement's region. A tiling T is a set of prototile placements whose regions have pairwise disjoint interiors. We say that the tiling T is a tiling of W where W is the union of the regions of the placements in T.A tile substitution is often loosely defined in the literature. A precise definition is as follows.
A tile substitution with respect to the prototiles P is a pair
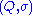 , where
, where 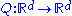 is a linear map, all of whose eigenvalues are larger than one in modulus, together with a substitution rule
is a linear map, all of whose eigenvalues are larger than one in modulus, together with a substitution rule  that maps each
that maps each 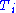 to a tiling of
to a tiling of 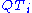 . The tile substitution
. The tile substitution  induces a map from any tiling T of a region W to a tiling
induces a map from any tiling T of a region W to a tiling 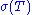 of
of  , defined by
, defined by
Note, that the prototiles can be deduced from the tile substitution. Therefore it is not necessary to include them in the tile substitution
 .
.Every tiling of
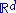 , where any finite part of it is congruent to a subset
, where any finite part of it is congruent to a subsetof some
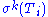 is called a substitution tiling (for the tile substitution
is called a substitution tiling (for the tile substitution 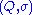 ).
).External links
- Dirk Frettlöh's and Edmund Harriss's Encyclopedia of Substitution Tilings