Pell's equation
Encyclopedia
Pell's equation is any Diophantine equation
of the form
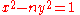
where n is a nonsquare
integer
. The word Diophantine means that integer values of x and y are sought. Trivially, x = 1 and y = 0 always solve this equation. Lagrange
proved that for any natural number
n that is not a perfect square
there are x and y > 0 that satisfy Pell's equation. Moreover, infinitely many such solutions of this equation exist. These solutions yield good rational
approximations of the form x/y to the square root
of n.
The name of this equation arose from Leonhard Euler
's mistakenly attributing
its study to John Pell
. Euler was aware of the work of Lord Brouncker, the first European mathematician to find a general solution of the equation, but apparently confused Brouncker with Pell. This equation was first studied extensively in ancient India
, starting with Brahmagupta
, who developed the chakravala method
to solve Pell's equation and other quadratic indeterminate equations in his Brahma Sphuta Siddhanta
in 628, about a thousand years before Pell's time. His Brahma Sphuta Siddhanta was translated into Arabic in 773
and was subsequently translated into Latin
in 1126. Bhaskara II in the 12th century and Narayana Pandit
in the 14th century both found general solutions to Pell's equation and other quadratic indeterminate equations. Solutions to specific examples of the Pell equation, such as the Pell number
s arising from the equation with n = 2, had been known for much longer, since the time of Pythagoras
in Greece
and to a similar date in India.
For a more detailed discussion of much of the material here, see Lenstra (2002) and Barbeau (2003).
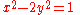
because of its connection to the square root of two. Indeed, if x and y are integers satisfying this equation, then x / y is an approximation of √2. For example, Baudhayana
discovered that x = 17, y = 12 and x = 577, y = 408 are two solutions to the Pell equation, and gave very close approximations to the square root of two.
Later, Archimedes used a similar equation to approximate the square root of 3, and found 1351/780.
Around AD 250, Diophantus
created a different form of the Pell equation
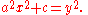
He solved this equation for a = 1, and c = −1, 1, and 12, and also solved for a = 3 and c = 9.
Brahmagupta
created a general way to solve Pell's equation known as the chakravala method
. Bhāskara I
created a way to create new solutions to Pell equations from one solution. E. Strachey published the work of Bhāskara I
in English in 1813. Alkarkhi
worked on similar problems to Diophantus.
Brahmagupta discovered that (see Brahmagupta's identity)
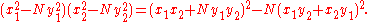
Using this, he was able to "compose" triples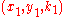
and 
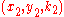that were solutions of 
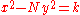, to generate the new triple
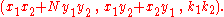
Not only did this give a way to generate infinitely many solutions to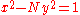
starting with one solution, but also, by dividing such a composition by 
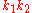, integer or "nearly integer" solutions could often be obtained. For instance, for 
, Brahmagupta composed the triple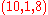 
(since 
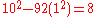) with itself to get the new triple 
. Dividing throughout by 64 gave the triple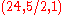 
, which when composed with itself gave the desired integer solution 
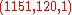. Brahmagupta solved many Pell equations with this method; in particular he showed how to obtain solutions starting from an integer solution of 
for k=±1, ±2, or ±4.
The first general method for solving the Pell equation (for all N) was given by Bhaskara II in 1150, extending the methods of Brahmagupta. Called the chakravala (cyclic) method
, it starts by composing any triple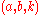
(that is, one which satisfies 
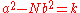) with the trivial triple 
to get the triple 
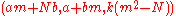, which can be scaled down to
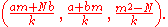
When m is chosen so that (a+bm)/k is an integer, so are the other two numbers in the triple. Among such m, the method chooses one that minimizes (m²-N)/k, and repeats the process. This method always terminates with a solution (proved by Lagrange in 1768). Bhaskara used it to give the solution x=1766319049, y=226153980 to the notorious N=61 case.
The general theory of Pell's equation, based on continued fractions and algebraic manipulations with numbers of the form
was developed by Lagrange
in 1766–1769.
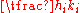denote the sequence of convergents
to the continued fraction
for
. Then the pair (x1,y1) solving Pell's equation and minimizing x satisfies x1 = hi and y1 = ki for some i. This pair is called the fundamental solution. Thus, the fundamental solution may be found by performing the continued fraction expansion and testing each successive convergent until a solution to Pell's equation is found.
As describes, the time for finding the fundamental solution using the continued fraction method, with the aid of the Schönhage–Strassen algorithm for fast integer multiplication, is within a logarithmic factor of the solution size, the number of digits in the pair (x1,y1). However, this is not a polynomial time algorithm because the number of digits in the solution may be as large as √n, far larger than a polynomial in the number of digits in the input value n .
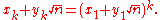
Equivalently, we may calculate subsequent solutions via the recurrence relation
s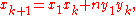
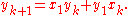
An alternative method to solving, once finding the first non-trivial solution, one could take the original equation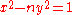
and factor the left hand side as a difference of squares, yielding 
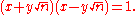Once in this form, one can simply raise each side of the equation to the kth power, and recombining the factored form to a single difference statement. The solution 
will be of the form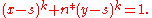 
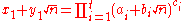
using much smaller coefficients ai, bi, and ci.
For instance, Archimedes' cattle problem
may be solved using a Pell equation, the fundamental solution of which has 206545 digits if written out explicitly. However, instead of writing the solution as a pair of numbers, it may be written using the formula
where
and
and 
only have 45 and 41 decimal digits, respectively. Alternatively, one may write even more concisely
.
Methods related to the quadratic sieve
approach for integer factorization
may be used to collect relations between prime numbers in the number field generated by √n, and to combine these relations to find a product representation of this type. The resulting algorithm for solving Pell's equation is more efficient than the continued fraction method, though it still does not take polynomial time. Under the assumption of the generalized Riemann hypothesis
, it can be shown to take time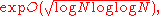
where N = log n is the input size, similarly to the quadratic sieve .
can find a product representation, as described above, for the solution to Pell's equation in polynomial time. Hallgren's algorithm, which can be interpreted as an algorithm for finding the group of units of a real quadratic number field, was extended to more general fields by .
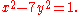
The sequence of convergents for the square root of seven are
Therefore, the fundamental solution is formed by the pair (8, 3). Applying the recurrence formula to this solution generates the infinite sequence of solutions
s, as the formula
is the norm
for the ring
and for the closely related quadratic field
. Thus, a pair of integers 
solves Pell's equation if and only if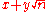 
is a unit
with norm 1 in
. Dirichlet's unit theorem
, that all units of
can be expressed as powers of a single fundamental unit
(and multiplication by a sign), is an algebraic restatement of the fact that all solutions to the Pell equation can be generated from the fundamental solution. The fundamental unit can in general be found by solving a Pell-like equation but it does not always correspond directly to the fundamental solution of Pell's equation itself.
:
If Ti (x) and Ui (x) are the Chebyshev polynomials of the first and second kind, respectively, then these polynomials satisfy a form of Pell's equation in any polynomial ring
R[x], with n = x2 − 1:
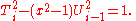
Thus, these polynomials can be generated by the standard technique for Pell equations of taking powers of a fundamental solution:
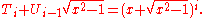
It may further be observed that, if (xi,yi) are the solutions to any integer Pell equation, then xi = Ti (x1) and yi = y1Ui − 1(x1) (Barbeau, chapter 3).
s can be presented, as the solutions x and y are approximates to the square root of n and thus are a special case of continued fraction approximations for quadratic irrational
s.
The relationship to the continued fractions implies that the solutions to Pell's equation form a semigroup
subset of the modular group
. Thus, for example, if p and q satisfy Pell's equation, then
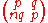
is a matrix of unit determinant
. Products of such matrices take exactly the same form, and thus all such products yield solutions to Pell's equation. This can be understood in part to arise from the fact that successive convergents of a continued fraction share the same property: If pk−1/qk−1 and pk/qk are two successive convergents of a continued fraction, then the matrix
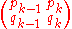
has determinant (−1)k.
Størmer's theorem
applies Pell equations to find pairs of consecutive smooth number
s. As part of this theory, Størmer
also investigated divisibility relations among solutions to Pell's equation; in particular, he showed that each solution other than the fundamental solution has a prime factor
that does not divide n.
As Lenstra (2002) describes, Pell's equation can also be used to solve Archimedes' cattle problem
.
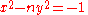(eq.1)
It has also been extensively studied; it can be solved by the same method of using continued fractions and will have solutions when the period of the continued fraction has odd length. However we do not know which roots have odd period lengths so we do not know when the negative Pell equation is solvable. But we can eliminate certain n since a necessary but not sufficient condition for solvability is that n is not divisible by a prime of form 4m+3. Thus, for example, x2-3py2 = -1 is never solvable, but x2-5py2 = -1 may be, such as when p = 1 or 13, though not when p = 41.
demonstrate that the proportion of square-free n for which the negative Pell equation is soluble is at least 40%. If it does have a solution, then it can be shown that its fundamental solution leads to the fundamental one for the positive case by squaring both sides of eq.1,
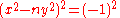
to get,
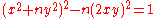
Or, since ny2 = x2+1 from eq.1, then,
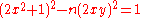
showing that fundamental solutions to the positive case are bigger than those for the negative case.
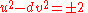(eq.2)
can be used to find solutions to the positive Pell equation for certain d. Legendre
proved that all primes of form d = 4m + 3 solve one case of eq.2, with the form 8m + 3 solving the negative, and 8m + 7 for the positive. Their fundamental solution then leads to the one for x2−dy2 = 1. This can be shown by squaring both sides of eq. 2,
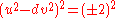
to get,
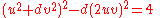
Since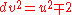
from eq.2, then,
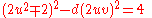
or simply,
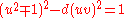
showing that fundamental solutions to eq.2 are smaller than eq.1. For example, u2-3v2 = -2 is {u,v} = {1,1}, so x2 − 3y2 = 1 has {x,y} = {2,1}. On the other hand, u2 − 7v2 = 2 is {u,v} = {3,1}, so x2 − 7y2 = 1 has {x,y} = {8,3}.
II. Another related equation,
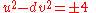(eq.3)
can also be used to find solutions to Pell equations for certain d, this time for the positive and negative case. For the following transformations, if fundamental {u,v} are both odd, then it leads to fundamental {x,y}.
1. If u2 − dv2 = −4, and {x,y} = {(u2 + 3)u/2, (u2 + 1)v/2}, then x2 − dy2 = −1.
Ex. Let d = 13, then {u,v} = {3, 1} and {x,y} = {18, 5}.
2. If u2 − dv2 = 4, and {x,y} = {(u2 − 3)u/2, (u2 − 1)v/2}, then x2 − dy2 = 1.
Ex. Let d = 13, then {u,v} = {11, 3} and {x,y} = {649, 180}.
3. If u2 − dv2 = −4, and {x,y} = {(u4 + 4u2 + 1)(u2 + 2)/2, (u2 + 3)(u2 + 1)uv/2}, then x2 − dy2 = 1.
Ex. Let d = 61, then {u,v} = {39, 5} and {x,y} = {1766319049, 226153980}.
Especially for the last transformation, it can be seen how solutions to {u,v} are much smaller than {x,y}, since the latter are sextic and quintic polynomials in terms of u.
Diophantine equation
In mathematics, a Diophantine equation is an indeterminate polynomial equation that allows the variables to be integers only. Diophantine problems have fewer equations than unknown variables and involve finding integers that work correctly for all equations...
of the form
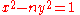
where n is a nonsquare
Square number
In mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
. The word Diophantine means that integer values of x and y are sought. Trivially, x = 1 and y = 0 always solve this equation. Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
proved that for any natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
n that is not a perfect square
Square number
In mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
there are x and y > 0 that satisfy Pell's equation. Moreover, infinitely many such solutions of this equation exist. These solutions yield good rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
approximations of the form x/y to the square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
of n.
The name of this equation arose from Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
's mistakenly attributing
Stigler's law of eponymy
Stigler's law of eponymy is a process proposed by University of Chicago statistics professor Stephen Stigler in his 1980 publication "Stigler’s law of eponymy". In its simplest and strongest form it says: "No scientific discovery is named after its original discoverer." Stigler named the...
its study to John Pell
John Pell
-Early life:He was born at Southwick in Sussex. He was educated at Steyning Grammar School, and entered Trinity College, Cambridge, at the age of thirteen. During his university career he became an accomplished linguist, and even before he took his B.A. degree corresponded with Henry Briggs and...
. Euler was aware of the work of Lord Brouncker, the first European mathematician to find a general solution of the equation, but apparently confused Brouncker with Pell. This equation was first studied extensively in ancient India
Indian mathematics
Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics , important contributions were made by scholars like Aryabhata, Brahmagupta, and Bhaskara II. The decimal number system in use today was first...
, starting with Brahmagupta
Brahmagupta
Brahmagupta was an Indian mathematician and astronomer who wrote many important works on mathematics and astronomy. His best known work is the Brāhmasphuṭasiddhānta , written in 628 in Bhinmal...
, who developed the chakravala method
Chakravala method
The chakravala method is a cyclic algorithm to solve indeterminate quadratic equations, including Pell's equation. It is commonly attributed to Bhāskara II, although some attribute it to Jayadeva...
to solve Pell's equation and other quadratic indeterminate equations in his Brahma Sphuta Siddhanta
Brahmasphutasiddhanta
The main work of Brahmagupta, Brāhmasphuṭasiddhānta , written c.628, contains ideas including a good understanding of the mathematical role of zero, rules for manipulating both negative and positive numbers, a method for computing square roots, methods of solving linear and some quadratic...
in 628, about a thousand years before Pell's time. His Brahma Sphuta Siddhanta was translated into Arabic in 773
773
Year 773 was a common year starting on Friday of the Julian calendar. The denomination 773 for this year has been used since the early medieval period, when the Anno Domini calendar era became the prevalent method in Europe for naming years.- Europe :* At request of the Pope Adrian I, Charlemagne...
and was subsequently translated into Latin
Latin
Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
in 1126. Bhaskara II in the 12th century and Narayana Pandit
Narayana Pandit
Narayana Pandita was a major mathematician of India. Plofker writes that his texts were the most significant Sanskrit mathematics treatises after those of Bhaskara II, other than the Kerala school. He wrote the Ganita Kaumudi in 1356 about mathematical operations. The work anticipated many...
in the 14th century both found general solutions to Pell's equation and other quadratic indeterminate equations. Solutions to specific examples of the Pell equation, such as the Pell number
Pell number
In mathematics, the Pell numbers are an infinite sequence of integers that have been known since ancient times, the denominators of the closest rational approximations to the square root of 2. This sequence of approximations begins 1/1, 3/2, 7/5, 17/12, and 41/29, so the sequence of Pell numbers...
s arising from the equation with n = 2, had been known for much longer, since the time of Pythagoras
Pythagoras
Pythagoras of Samos was an Ionian Greek philosopher, mathematician, and founder of the religious movement called Pythagoreanism. Most of the information about Pythagoras was written down centuries after he lived, so very little reliable information is known about him...
in Greece
Greek mathematics
Greek mathematics, as that term is used in this article, is the mathematics written in Greek, developed from the 7th century BC to the 4th century AD around the Eastern shores of the Mediterranean. Greek mathematicians lived in cities spread over the entire Eastern Mediterranean, from Italy to...
and to a similar date in India.
For a more detailed discussion of much of the material here, see Lenstra (2002) and Barbeau (2003).
History
Pell's equations were studied as early as 400 BC in India and Greece. They were mainly interested in the equation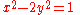because of its connection to the square root of two. Indeed, if x and y are integers satisfying this equation, then x / y is an approximation of √2. For example, Baudhayana
Baudhayana
Baudhāyana, was an Indian mathematician, whowas most likely also a priest. He is noted as the author of the earliest Sulba Sūtra—appendices to the Vedas giving rules for the construction of altars—called the , which contained several important mathematical results. He is older than the other...
discovered that x = 17, y = 12 and x = 577, y = 408 are two solutions to the Pell equation, and gave very close approximations to the square root of two.
Later, Archimedes used a similar equation to approximate the square root of 3, and found 1351/780.
Around AD 250, Diophantus
Diophantus
Diophantus of Alexandria , sometimes called "the father of algebra", was an Alexandrian Greek mathematician and the author of a series of books called Arithmetica. These texts deal with solving algebraic equations, many of which are now lost...
created a different form of the Pell equation
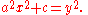
He solved this equation for a = 1, and c = −1, 1, and 12, and also solved for a = 3 and c = 9.
Brahmagupta
Brahmagupta
Brahmagupta was an Indian mathematician and astronomer who wrote many important works on mathematics and astronomy. His best known work is the Brāhmasphuṭasiddhānta , written in 628 in Bhinmal...
created a general way to solve Pell's equation known as the chakravala method
Chakravala method
The chakravala method is a cyclic algorithm to solve indeterminate quadratic equations, including Pell's equation. It is commonly attributed to Bhāskara II, although some attribute it to Jayadeva...
. Bhāskara I
Bhaskara I
Bhāskara was a 7th century Indian mathematician, who was apparently the first to write numbers in the Hindu-Arabic decimal system with a circle for the zero, and who gave a unique and remarkable rational approximation of the sine function in his commentary on Aryabhata's work...
created a way to create new solutions to Pell equations from one solution. E. Strachey published the work of Bhāskara I
Bhaskara I
Bhāskara was a 7th century Indian mathematician, who was apparently the first to write numbers in the Hindu-Arabic decimal system with a circle for the zero, and who gave a unique and remarkable rational approximation of the sine function in his commentary on Aryabhata's work...
in English in 1813. Alkarkhi
Al-Karaji
' was a 10th century Persian Muslim mathematician and engineer. His three major works are Al-Badi' fi'l-hisab , Al-Fakhri fi'l-jabr wa'l-muqabala , and Al-Kafi fi'l-hisab .Because al-Karaji's original works in Arabic are lost, it is not...
worked on similar problems to Diophantus.
Brahmagupta discovered that (see Brahmagupta's identity)
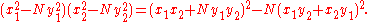
Using this, he was able to "compose" triples
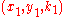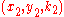and that were solutions of 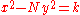, to generate the new triple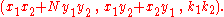Not only did this give a way to generate infinitely many solutions to
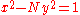starting with one solution, but also, by dividing such a composition by 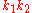, integer or "nearly integer" solutions could often be obtained. For instance, for , Brahmagupta composed the triple 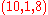(since 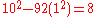) with itself to get the new triple . Dividing throughout by 64 gave the triple 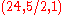, which when composed with itself gave the desired integer solution 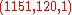. Brahmagupta solved many Pell equations with this method; in particular he showed how to obtain solutions starting from an integer solution of for k=±1, ±2, or ±4.The first general method for solving the Pell equation (for all N) was given by Bhaskara II in 1150, extending the methods of Brahmagupta. Called the chakravala (cyclic) method
Chakravala method
The chakravala method is a cyclic algorithm to solve indeterminate quadratic equations, including Pell's equation. It is commonly attributed to Bhāskara II, although some attribute it to Jayadeva...
, it starts by composing any triple
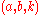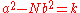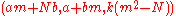(that is, one which satisfies ) with the trivial triple to get the triple , which can be scaled down to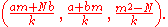When m is chosen so that (a+bm)/k is an integer, so are the other two numbers in the triple. Among such m, the method chooses one that minimizes (m²-N)/k, and repeats the process. This method always terminates with a solution (proved by Lagrange in 1768). Bhaskara used it to give the solution x=1766319049, y=226153980 to the notorious N=61 case.
The general theory of Pell's equation, based on continued fractions and algebraic manipulations with numbers of the form
was developed by LagrangeJoseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
in 1766–1769.
Fundamental solution via continued fractions
Let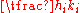 denote the sequence of convergentsConvergent (continued fraction)
A convergent is one of a sequence of values obtained by evaluating successive truncations of a continued fraction The nth convergent is also known as the nth approximant of a continued fraction.-Representation of real numbers:...
to the continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
for
. Then the pair (x1,y1) solving Pell's equation and minimizing x satisfies x1 = hi and y1 = ki for some i. This pair is called the fundamental solution. Thus, the fundamental solution may be found by performing the continued fraction expansion and testing each successive convergent until a solution to Pell's equation is found.As describes, the time for finding the fundamental solution using the continued fraction method, with the aid of the Schönhage–Strassen algorithm for fast integer multiplication, is within a logarithmic factor of the solution size, the number of digits in the pair (x1,y1). However, this is not a polynomial time algorithm because the number of digits in the solution may be as large as √n, far larger than a polynomial in the number of digits in the input value n .
Additional solutions from the fundamental solution
Once the fundamental solution is found, all remaining solutions may be calculated algebraically as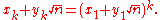Equivalently, we may calculate subsequent solutions via the recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
s
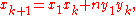
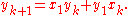
An alternative method to solving, once finding the first non-trivial solution, one could take the original equation
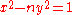and factor the left hand side as a difference of squares, yielding 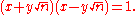Once in this form, one can simply raise each side of the equation to the kth power, and recombining the factored form to a single difference statement. The solution will be of the form 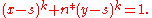Concise representation and faster algorithms
Although writing out the fundamental solution (x1,y1) as a pair of binary numbers may require a large number of bits, it may in many cases be represented more compactly in the form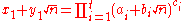using much smaller coefficients ai, bi, and ci.
For instance, Archimedes' cattle problem
Archimedes' cattle problem
Archimedes' cattle problem is a problem in Diophantine analysis, the study of polynomial equations with integer solutions. Attributed to Archimedes, the problem involves computing the number of cattle in a herd of the sun god from a given set of restrictions...
may be solved using a Pell equation, the fundamental solution of which has 206545 digits if written out explicitly. However, instead of writing the solution as a pair of numbers, it may be written using the formula
where
and
and only have 45 and 41 decimal digits, respectively. Alternatively, one may write even more concisely.
Methods related to the quadratic sieve
Quadratic sieve
The quadratic sieve algorithm is a modern integer factorization algorithm and, in practice, the second fastest method known . It is still the fastest for integers under 100 decimal digits or so, and is considerably simpler than the number field sieve...
approach for integer factorization
Integer factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
may be used to collect relations between prime numbers in the number field generated by √n, and to combine these relations to find a product representation of this type. The resulting algorithm for solving Pell's equation is more efficient than the continued fraction method, though it still does not take polynomial time. Under the assumption of the generalized Riemann hypothesis
Generalized Riemann hypothesis
The Riemann hypothesis is one of the most important conjectures in mathematics. It is a statement about the zeros of the Riemann zeta function. Various geometrical and arithmetical objects can be described by so-called global L-functions, which are formally similar to the Riemann zeta-function...
, it can be shown to take time
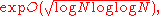
where N = log n is the input size, similarly to the quadratic sieve .
Quantum algorithms
showed that a quantum computerQuantum computer
A quantum computer is a device for computation that makes direct use of quantum mechanical phenomena, such as superposition and entanglement, to perform operations on data. Quantum computers are different from traditional computers based on transistors...
can find a product representation, as described above, for the solution to Pell's equation in polynomial time. Hallgren's algorithm, which can be interpreted as an algorithm for finding the group of units of a real quadratic number field, was extended to more general fields by .
Example
As an example, consider the instance of Pell's equation for n = 7; that is,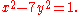The sequence of convergents for the square root of seven are
| h / k (Convergent) | h2 −7k2 (Pell-type approximation) |
|---|---|
| 2 / 1 | −3 |
| 3 / 1 | +2 |
| 5 / 2 | −3 |
| 8 / 3 | +1 |
Therefore, the fundamental solution is formed by the pair (8, 3). Applying the recurrence formula to this solution generates the infinite sequence of solutions
- (127, 48); (2024, 765); (32257, 12192); (514088, 194307); (8193151; 3096720); (130576328, 49353213); ..
Algebraic number theory
Pell's equation is closely related to the theory of algebraic numberAlgebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s, as the formula
is the norm
Field norm
In mathematics, the norm is a mapping defined in field theory, to map elements of a larger field into a smaller one.-Formal definitions:1. Let K be a field and L a finite extension of K...
for the ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
and for the closely related quadratic fieldQuadratic field
In algebraic number theory, a quadratic field is an algebraic number field K of degree two over Q. It is easy to show that the map d ↦ Q is a bijection from the set of all square-free integers d ≠ 0, 1 to the set of all quadratic fields...
. Thus, a pair of integers solves Pell's equation if and only if 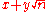is a unitUnit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
with norm 1 in
. Dirichlet's unit theoremDirichlet's unit theorem
In mathematics, Dirichlet's unit theorem is a basic result in algebraic number theory due to Gustav Lejeune Dirichlet. It determines the rank of the group of units in the ring OK of algebraic integers of a number field K...
, that all units of
can be expressed as powers of a single fundamental unitFundamental unit (number theory)
In algebraic number theory, a fundamental unit is a generator for the torsion-free unit group of the ring of integers of a number field, when that group is infinite cyclic...
(and multiplication by a sign), is an algebraic restatement of the fact that all solutions to the Pell equation can be generated from the fundamental solution. The fundamental unit can in general be found by solving a Pell-like equation but it does not always correspond directly to the fundamental solution of Pell's equation itself.
Chebyshev polynomials
Demeyer (2007) mentions a connection between Pell's equation and the Chebyshev polynomialsChebyshev polynomials
In mathematics the Chebyshev polynomials, named after Pafnuty Chebyshev, are a sequence of orthogonal polynomials which are related to de Moivre's formula and which can be defined recursively. One usually distinguishes between Chebyshev polynomials of the first kind which are denoted Tn and...
:
If Ti (x) and Ui (x) are the Chebyshev polynomials of the first and second kind, respectively, then these polynomials satisfy a form of Pell's equation in any polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
R[x], with n = x2 − 1:
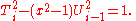
Thus, these polynomials can be generated by the standard technique for Pell equations of taking powers of a fundamental solution:
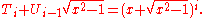
It may further be observed that, if (xi,yi) are the solutions to any integer Pell equation, then xi = Ti (x1) and yi = y1Ui − 1(x1) (Barbeau, chapter 3).
Continued fractions
A general development of solutions of Pell's equation in terms of continued fractionContinued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
s can be presented, as the solutions x and y are approximates to the square root of n and thus are a special case of continued fraction approximations for quadratic irrational
Quadratic irrational
In mathematics, a quadratic irrational is an irrational number that is the solution to some quadratic equation with rational coefficients...
s.
The relationship to the continued fractions implies that the solutions to Pell's equation form a semigroup
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
subset of the modular group
Modular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
. Thus, for example, if p and q satisfy Pell's equation, then
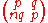
is a matrix of unit determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
. Products of such matrices take exactly the same form, and thus all such products yield solutions to Pell's equation. This can be understood in part to arise from the fact that successive convergents of a continued fraction share the same property: If pk−1/qk−1 and pk/qk are two successive convergents of a continued fraction, then the matrix
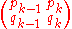
has determinant (−1)k.
Størmer's theorem
Størmer's theorem
In number theory, Størmer's theorem, named after Carl Størmer, gives a finite bound on the number of consecutive pairs of smooth numbers that exist, for a given degree of smoothness, and provides a method for finding all such pairs using Pell equations...
applies Pell equations to find pairs of consecutive smooth number
Smooth number
In number theory, a smooth number is an integer which factors completely into small prime numbers. The term seems to have been coined by Leonard Adleman. Smooth numbers are especially important in cryptography relying on factorization.-Definition:...
s. As part of this theory, Størmer
Carl Størmer
Fredrik Carl Mülertz Størmer was a Norwegian mathematician and physicist, known both for his work in number theory and for studying the movement of charged particles in the magnetosphere and the formation of aurorae....
also investigated divisibility relations among solutions to Pell's equation; in particular, he showed that each solution other than the fundamental solution has a prime factor
Prime factor
In number theory, the prime factors of a positive integer are the prime numbers that divide that integer exactly, without leaving a remainder. The process of finding these numbers is called integer factorization, or prime factorization. A prime factor can be visualized by understanding Euclid's...
that does not divide n.
As Lenstra (2002) describes, Pell's equation can also be used to solve Archimedes' cattle problem
Archimedes' cattle problem
Archimedes' cattle problem is a problem in Diophantine analysis, the study of polynomial equations with integer solutions. Attributed to Archimedes, the problem involves computing the number of cattle in a herd of the sun god from a given set of restrictions...
.
The negative Pell equation
The negative Pell equation is given by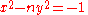 (eq.1)It has also been extensively studied; it can be solved by the same method of using continued fractions and will have solutions when the period of the continued fraction has odd length. However we do not know which roots have odd period lengths so we do not know when the negative Pell equation is solvable. But we can eliminate certain n since a necessary but not sufficient condition for solvability is that n is not divisible by a prime of form 4m+3. Thus, for example, x2-3py2 = -1 is never solvable, but x2-5py2 = -1 may be, such as when p = 1 or 13, though not when p = 41.
demonstrate that the proportion of square-free n for which the negative Pell equation is soluble is at least 40%. If it does have a solution, then it can be shown that its fundamental solution leads to the fundamental one for the positive case by squaring both sides of eq.1,
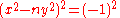
to get,
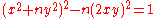
Or, since ny2 = x2+1 from eq.1, then,
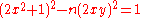
showing that fundamental solutions to the positive case are bigger than those for the negative case.
Transformations
I. The related equation,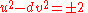 (eq.2)can be used to find solutions to the positive Pell equation for certain d. Legendre
Adrien-Marie Legendre
Adrien-Marie Legendre was a French mathematician.The Moon crater Legendre is named after him.- Life :...
proved that all primes of form d = 4m + 3 solve one case of eq.2, with the form 8m + 3 solving the negative, and 8m + 7 for the positive. Their fundamental solution then leads to the one for x2−dy2 = 1. This can be shown by squaring both sides of eq. 2,
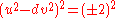
to get,
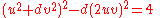
Since
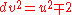from eq.2, then,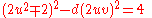or simply,
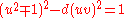
showing that fundamental solutions to eq.2 are smaller than eq.1. For example, u2-3v2 = -2 is {u,v} = {1,1}, so x2 − 3y2 = 1 has {x,y} = {2,1}. On the other hand, u2 − 7v2 = 2 is {u,v} = {3,1}, so x2 − 7y2 = 1 has {x,y} = {8,3}.
II. Another related equation,
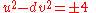(eq.3)can also be used to find solutions to Pell equations for certain d, this time for the positive and negative case. For the following transformations, if fundamental {u,v} are both odd, then it leads to fundamental {x,y}.
1. If u2 − dv2 = −4, and {x,y} = {(u2 + 3)u/2, (u2 + 1)v/2}, then x2 − dy2 = −1.
Ex. Let d = 13, then {u,v} = {3, 1} and {x,y} = {18, 5}.
2. If u2 − dv2 = 4, and {x,y} = {(u2 − 3)u/2, (u2 − 1)v/2}, then x2 − dy2 = 1.
Ex. Let d = 13, then {u,v} = {11, 3} and {x,y} = {649, 180}.
3. If u2 − dv2 = −4, and {x,y} = {(u4 + 4u2 + 1)(u2 + 2)/2, (u2 + 3)(u2 + 1)uv/2}, then x2 − dy2 = 1.
Ex. Let d = 61, then {u,v} = {39, 5} and {x,y} = {1766319049, 226153980}.
Especially for the last transformation, it can be seen how solutions to {u,v} are much smaller than {x,y}, since the latter are sextic and quintic polynomials in terms of u.
External links
- IMO Compendium text on Pell's equation in problem solving.