
Smooth number
Encyclopedia
In number theory
, a smooth number is an integer
which factors
completely into small prime number
s. The term seems to have been coined by Leonard Adleman
. Smooth numbers are especially important in cryptography
relying on factorization.
is called B-smooth if none of its prime factor
s is greater than B. For example, 1,620 has prime factorization 22 × 34 × 5; therefore 1,620 is 5-smooth because none of its prime factors is greater than 5. It is worth note that this definition includes numbers that lack some of the smaller prime factors. For example, both 10 and 12 are 5-smooth, despite the fact that they miss out prime factors 3 and 5 respectively. 5-smooth numbers are also called regular number
s or Hamming numbers; 7-smooth numbers are sometimes called highly composite, although this conflicts with another meaning of that term
.
Note that B does not have to be a prime factor. If the largest prime factor of a number is p then the number is B-smooth for any B ≥ p. Usually B is given as a prime, but composite number
s work as well. A number is B-smooth if and only if
it is p-smooth, where p is the largest prime less than or equal to B.
(FFT) algorithms such as the Cooley–Tukey FFT algorithm that operate by recursively breaking down a problem of a given size n into problems the size of its factors. By using B-smooth numbers, one ensures that the base cases of this recursion are small primes, for which efficient algorithms exist. (Large prime sizes require less-efficient algorithms such as Bluestein's FFT algorithm
.)
5-smooth or regular number
s play a special role in Babylonian mathematics
. They are also important in music theory
, (see Limit (music)
) and the problem of generating these numbers efficiently has been used as a test problem for functional programming
.
Smooth numbers have a number of applications to cryptography. Although most applications involve cryptanalysis, the VSH
hash function is one example of a constructive use of smoothness to obtain a provably secure design
.
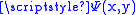 denote the number of y-smooth integers less than or equal to x (the de Bruijn function).
denote the number of y-smooth integers less than or equal to x (the de Bruijn function).
If the smoothness bound B is fixed and small, there is a good estimate for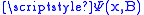 :
:
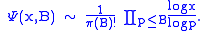
Otherwise, define the parameter u as u = log x / log y: that is, x = yu. Then,
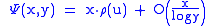
where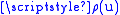 is the Dickman function.
is the Dickman function.
 dividing m satisfy:
dividing m satisfy:
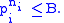
For example, 243251 is 16-powersmooth since its greatest prime factor power is 24 = 16. The number is also 17-powersmooth, 18-powersmooth, 19-powersmooth, etc.
B-smooth and B-powersmooth numbers have applications in number theory, such as in Pollard's p − 1 algorithm. Such applications are often said to work with "smooth numbers," with no B specified; this means the numbers involved must be B-smooth for some unspecified small number B; as B increases, the performance of the algorithm or method in question degrades rapidly. For example, the Pohlig–Hellman algorithm for computing discrete logarithm
s has a running time of O(B1/2) for group
s of B-smooth order.
(OEIS)
lists B-smooth numbers for small Bs:
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, a smooth number is an integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
which factors
Integer factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
completely into small prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s. The term seems to have been coined by Leonard Adleman
Leonard Adleman
Leonard Max Adleman is an American theoretical computer scientist and professor of computer science and molecular biology at the University of Southern California. He is known for being a co-inventor of the RSA cryptosystem in 1977, and of DNA computing...
. Smooth numbers are especially important in cryptography
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
relying on factorization.
Definition
A positive integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
is called B-smooth if none of its prime factor
Prime factor
In number theory, the prime factors of a positive integer are the prime numbers that divide that integer exactly, without leaving a remainder. The process of finding these numbers is called integer factorization, or prime factorization. A prime factor can be visualized by understanding Euclid's...
s is greater than B. For example, 1,620 has prime factorization 22 × 34 × 5; therefore 1,620 is 5-smooth because none of its prime factors is greater than 5. It is worth note that this definition includes numbers that lack some of the smaller prime factors. For example, both 10 and 12 are 5-smooth, despite the fact that they miss out prime factors 3 and 5 respectively. 5-smooth numbers are also called regular number
Regular number
Regular numbers are numbers that evenly divide powers of 60. As an example, 602 = 3600 = 48 × 75, so both 48 and 75 are divisors of a power of 60...
s or Hamming numbers; 7-smooth numbers are sometimes called highly composite, although this conflicts with another meaning of that term
Highly composite number
A highly composite number is a positive integer with more divisors than any positive integer smaller than itself.The initial or smallest twenty-one highly composite numbers are listed in the table at right....
.
Note that B does not have to be a prime factor. If the largest prime factor of a number is p then the number is B-smooth for any B ≥ p. Usually B is given as a prime, but composite number
Composite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
s work as well. A number is B-smooth if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it is p-smooth, where p is the largest prime less than or equal to B.
Applications
An important practical application of smooth numbers is for fast Fourier transformFast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
(FFT) algorithms such as the Cooley–Tukey FFT algorithm that operate by recursively breaking down a problem of a given size n into problems the size of its factors. By using B-smooth numbers, one ensures that the base cases of this recursion are small primes, for which efficient algorithms exist. (Large prime sizes require less-efficient algorithms such as Bluestein's FFT algorithm
Bluestein's FFT algorithm
Bluestein's FFT algorithm , commonly called the chirp z-transform algorithm , is a fast Fourier transform algorithm that computes the discrete Fourier transform of arbitrary sizes by re-expressing the DFT as a convolution...
.)
5-smooth or regular number
Regular number
Regular numbers are numbers that evenly divide powers of 60. As an example, 602 = 3600 = 48 × 75, so both 48 and 75 are divisors of a power of 60...
s play a special role in Babylonian mathematics
Babylonian mathematics
Babylonian mathematics refers to any mathematics of the people of Mesopotamia, from the days of the early Sumerians to the fall of Babylon in 539 BC. Babylonian mathematical texts are plentiful and well edited...
. They are also important in music theory
Music theory
Music theory is the study of how music works. It examines the language and notation of music. It seeks to identify patterns and structures in composers' techniques across or within genres, styles, or historical periods...
, (see Limit (music)
Limit (music)
In music theory, limit or harmonic limit is a way of characterizing the harmony found in a piece or genre of music, or the harmonies that can be made using a particular scale. The term was introduced by Harry Partch, who used it to give an upper bound on the complexity of harmony; hence the name...
) and the problem of generating these numbers efficiently has been used as a test problem for functional programming
Functional programming
In computer science, functional programming is a programming paradigm that treats computation as the evaluation of mathematical functions and avoids state and mutable data. It emphasizes the application of functions, in contrast to the imperative programming style, which emphasizes changes in state...
.
Smooth numbers have a number of applications to cryptography. Although most applications involve cryptanalysis, the VSH
Very smooth hash
In cryptography, Very Smooth Hash is a secure cryptographic hash function invented in 2005 by Scott Contini, Arjen Lenstra and Ron Steinfeld....
hash function is one example of a constructive use of smoothness to obtain a provably secure design
Provably secure cryptographic hash function
In cryptography, cryptographic hash functions can be divided into two main categories. In the first category are those functions whose designs are based on a mathematical problem and thus their security follows from rigorous mathematical proofs, complexity theory and formal reduction. These...
.
Distribution
Let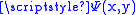 denote the number of y-smooth integers less than or equal to x (the de Bruijn function).
denote the number of y-smooth integers less than or equal to x (the de Bruijn function).If the smoothness bound B is fixed and small, there is a good estimate for
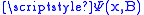 :
: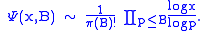
Otherwise, define the parameter u as u = log x / log y: that is, x = yu. Then,
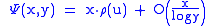
where
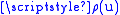 is the Dickman function.
is the Dickman function.Powersmooth numbers
Further, m is called B-powersmooth if all prime powers dividing m satisfy:
dividing m satisfy: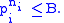
For example, 243251 is 16-powersmooth since its greatest prime factor power is 24 = 16. The number is also 17-powersmooth, 18-powersmooth, 19-powersmooth, etc.
B-smooth and B-powersmooth numbers have applications in number theory, such as in Pollard's p − 1 algorithm. Such applications are often said to work with "smooth numbers," with no B specified; this means the numbers involved must be B-smooth for some unspecified small number B; as B increases, the performance of the algorithm or method in question degrades rapidly. For example, the Pohlig–Hellman algorithm for computing discrete logarithm
Discrete logarithm
In mathematics, specifically in abstract algebra and its applications, discrete logarithms are group-theoretic analogues of ordinary logarithms. In particular, an ordinary logarithm loga is a solution of the equation ax = b over the real or complex numbers...
s has a running time of O(B1/2) for group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
s of B-smooth order.
External links
The On-Line Encyclopedia of Integer SequencesOn-Line Encyclopedia of Integer Sequences
The On-Line Encyclopedia of Integer Sequences , also cited simply as Sloane's, is an online database of integer sequences, created and maintained by N. J. A. Sloane, a researcher at AT&T Labs...
(OEIS)
lists B-smooth numbers for small Bs:
- 2-smooth numbers: A000079 (2i)
- 3-smooth numbers: A003586 (2i3j)
- 5-smooth numbers: A051037 (2i3j5k)
- 7-smooth numbers: A002473 (2i3j5k7l)
- 11-smooth numbers: A051038 (etc...)
- 13-smooth numbers: A080197
- 17-smooth numbers: A080681
- 19-smooth numbers: A080682
- 23-smooth numbers: A080683

