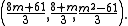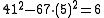Chakravala method
Encyclopedia
The chakravala method is a cyclic algorithm
to solve indeterminate
quadratic equation
s, including Pell's equation
. It is commonly attributed to Bhāskara II, (c. 1114 – 1185 CE) although some attribute it to Jayadeva
(c. 950 ~ 1000 CE). Jayadeva pointed out that Brahmagupta
's approach to solving equations of this type could be generalized, and he then described this general method, which was later refined by Bhāskara II in his Bijaganita
treatise. He called it the Chakravala method: chakra meaning "wheel" in Sanskrit
, a reference to the cyclic nature of the algorithm. E. O. Selenius held that no European performances at the time of Bhāskara, nor much later, exceeded its marvellous height of mathematical complexity.
This method is also known as the cyclic method and contains traces of mathematical induction
.
in 628 CE studied indeterminate quadratic equations, including Pell's equation
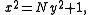
for minimum integers x and y. Brahmagupta could solve it for several N, but not all.
Jayadeva (9th century) and Bhaskara (12th century) offered the first complete solution to the equation, using the chakravala method to find (for the notorious N = 61 case)
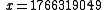and 
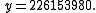
This case was first solved in Europe
by Brouncker in 1657–58 in response to a challenge by Fermat
, and a method first completely described by Lagrange
in 1766. Lagrange's method, however, requires the calculation of 21 successive convergents of the continued fraction
for the square root
of 61, while the chakravala method is much simpler. Selenius, in his assessment of the chakravala method, states
Hermann Hankel
calls the chakravala method
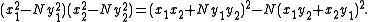
This defines a "composition" (samāsa) of two triples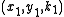
and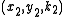 
that are solutions of 
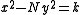, to generate the new triple
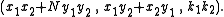
In the general method, the main idea is that any triple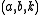
(that is, one which satisfies 
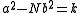) can be composed with the trivial triple 
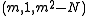to get the new triple 
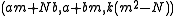for any m. Assuming we started with a triple for which 
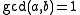, this can be scaled down by k (this is Bhaskara's lemma):
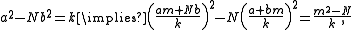
or, since the signs inside the squares do not matter,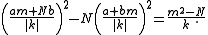
When a positive integer m is chosen so that (a + bm)/k is an integer, so are the other two numbers in the triple. Among such m, the method chooses one that minimizes the absolute value of m2 − N and hence that of (m2 − N)/k. Then, (a, b, k) is replaced with the new triple given by the above equation, and the process is repeated. This method always terminates with a solution (proved by Lagrange in 1768).
Optionally, we can stop when k is ±1, ±2, or ±4, as Brahmagupta's approach gives a solution for those cases.
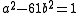), issued as a challenge by Fermat many centuries later, was given by Bhaskara as an example.
We start with a solution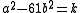
for any k found by any means. In this case we can let b be 1, thus, since 
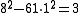, we have the triple 
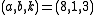. Composing it with 
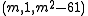gives the triple 
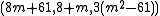, which is scaled down (or Bhaskara's lemma is directly used) to get:
For 3 to divide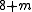
and 
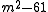to be minimal, we choose m=7, so that we have the triple 
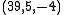. Now that k is −4, we can use Brahmagupta's idea: it can be scaled down to the rational solution 
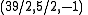, which composed with itself twice gives 
and then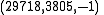 
. Finally, this is composed with itself, giving the solution 
. This is the minimal integer solution.
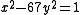for x and y.
We start with a solution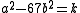
for any k found by any means; in this case we can let b be 1, thus producing 
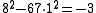. At each step, we find an m > 0 such that k divides 
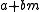, and 
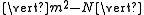is minimal. We then update a, b, and k to 
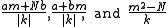respectively.
First iteration
We have a = 8, b = 1, k = −3. We want a positive integer m such that k divides a+mb, i.e. 3 divides 8+m, and
is minimal. The first condition implies that m is of the form 3t+1 (i.e. 1, 4, 7, 10,… etc.), and among such m, the minimal value is attained for m=7. Replacing (a, b, k) with (am+Nb)/|k|, (a + bm)/|k|, and (m2 − N)/k, we get the new values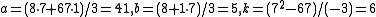 
. That is, we have the new solution:
At this point, one round of the cyclic algorithm is complete.
Second iteration
We now repeat the process. We have a = 41, b = 5, k = 6. We want an m > 0 such that k divides a + mb, i.e. 6 divides 41 + 5m, and |m2 − 67| is minimal. The first condition implies that m is of the form 6t + 5 (i.e. 5, 11, 17,…), and among such m, |m2 − 67| is minimal for m = 5. This leads to the new solution a = (41⋅5 + 67⋅5)/6, etc.:
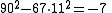
Third iteration
For 7 to divide 90+11m, we must have m = 2 + 7t (2, 9, 16,…) and among such m, we pick m=9.
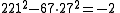
Final solution
At this point, we could continue with the cyclic method (and it would end, after seven iterations), but since the right-hand side is among ±1, ±2, ±4, we can also use Brahmagupta's observation directly. Composing the triple (221, 27, −2) with itself, we get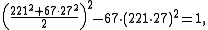
that is, we have the integer solution: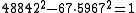
This equation approximates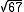
(as 48842/5967) to within a margin of about 
.
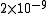Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
to solve indeterminate
Indeterminate equation
An indeterminate equation, in mathematics, is an equation for which there is an infinite set of solutions; for example, 2x = y is a simple indeterminate equation. Indeterminate equations cannot be directly solved from the given information...
quadratic equation
Quadratic equation
In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...
s, including Pell's equation
Pell's equation
Pell's equation is any Diophantine equation of the formx^2-ny^2=1\,where n is a nonsquare integer. The word Diophantine means that integer values of x and y are sought. Trivially, x = 1 and y = 0 always solve this equation...
. It is commonly attributed to Bhāskara II, (c. 1114 – 1185 CE) although some attribute it to Jayadeva
Jayadeva (mathematician)
Jayadeva was a ninth-century Indian mathematician, who further developed the cyclic method that was called by Hermann Hankel the finest thing achieved in the theory of numbers before Lagrange . He also made significant contributions to combinatorics....
(c. 950 ~ 1000 CE). Jayadeva pointed out that Brahmagupta
Brahmagupta
Brahmagupta was an Indian mathematician and astronomer who wrote many important works on mathematics and astronomy. His best known work is the Brāhmasphuṭasiddhānta , written in 628 in Bhinmal...
's approach to solving equations of this type could be generalized, and he then described this general method, which was later refined by Bhāskara II in his Bijaganita
Bijaganita
Bijaganita was Indian mathematician Bhāskara II's treatise on algebra. It is the second volume of his main work Siddhānta Shiromani, Sanskrit for "Crown of treatises," alongside Lilāvati, Grahaganita and Golādhyāya.- Contents :...
treatise. He called it the Chakravala method: chakra meaning "wheel" in Sanskrit
Sanskrit
Sanskrit , is a historical Indo-Aryan language and the primary liturgical language of Hinduism, Jainism and Buddhism.Buddhism: besides Pali, see Buddhist Hybrid Sanskrit Today, it is listed as one of the 22 scheduled languages of India and is an official language of the state of Uttarakhand...
, a reference to the cyclic nature of the algorithm. E. O. Selenius held that no European performances at the time of Bhāskara, nor much later, exceeded its marvellous height of mathematical complexity.
This method is also known as the cyclic method and contains traces of mathematical induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
.
History
BrahmaguptaBrahmagupta
Brahmagupta was an Indian mathematician and astronomer who wrote many important works on mathematics and astronomy. His best known work is the Brāhmasphuṭasiddhānta , written in 628 in Bhinmal...
in 628 CE studied indeterminate quadratic equations, including Pell's equation
Pell's equation
Pell's equation is any Diophantine equation of the formx^2-ny^2=1\,where n is a nonsquare integer. The word Diophantine means that integer values of x and y are sought. Trivially, x = 1 and y = 0 always solve this equation...
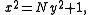
for minimum integers x and y. Brahmagupta could solve it for several N, but not all.
Jayadeva (9th century) and Bhaskara (12th century) offered the first complete solution to the equation, using the chakravala method to find (for the notorious N = 61 case)
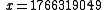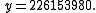
and This case was first solved in Europe
Europe
Europe is, by convention, one of the world's seven continents. Comprising the westernmost peninsula of Eurasia, Europe is generally 'divided' from Asia to its east by the watershed divides of the Ural and Caucasus Mountains, the Ural River, the Caspian and Black Seas, and the waterways connecting...
by Brouncker in 1657–58 in response to a challenge by Fermat
Pierre de Fermat
Pierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...
, and a method first completely described by Lagrange
Lagrange
La Grange literally means the barn in French. Lagrange may refer to:- People :* Charles Varlet de La Grange , French actor* Georges Lagrange , translator to and writer in Esperanto...
in 1766. Lagrange's method, however, requires the calculation of 21 successive convergents of the continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
for the square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
of 61, while the chakravala method is much simpler. Selenius, in his assessment of the chakravala method, states
- "The method represents a best approximation algorithm of minimal length that, owing to several minimization properties, with minimal effort and avoiding large numbers automatically produces the best solutions to the equation. The chakravala method anticipated the European methods by more than a thousand years. But no European performances in the whole field of algebraAlgebraAlgebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
at a time much later than Bhaskara's, nay nearly equal up to our times, equalled the marvellous complexity and ingenuity of chakravala."
Hermann Hankel
Hermann Hankel
Hermann Hankel was a German mathematician who was born in Halle, Germany and died in Schramberg , Imperial Germany....
calls the chakravala method
- "the finest thing achieved in the theory of numbers before Lagrange."
The method
The chakravala method for solving Pell's equation is based on the observation by Brahmagupta (see Brahmagupta's identity) that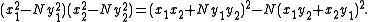This defines a "composition" (samāsa) of two triples
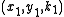and 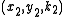that are solutions of 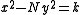, to generate the new triple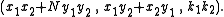In the general method, the main idea is that any triple
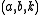(that is, one which satisfies 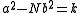) can be composed with the trivial triple 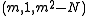to get the new triple 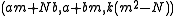for any m. Assuming we started with a triple for which 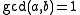, this can be scaled down by k (this is Bhaskara's lemma):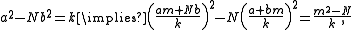or, since the signs inside the squares do not matter,
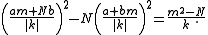
When a positive integer m is chosen so that (a + bm)/k is an integer, so are the other two numbers in the triple. Among such m, the method chooses one that minimizes the absolute value of m2 − N and hence that of (m2 − N)/k. Then, (a, b, k) is replaced with the new triple given by the above equation, and the process is repeated. This method always terminates with a solution (proved by Lagrange in 1768).
Optionally, we can stop when k is ±1, ±2, or ±4, as Brahmagupta's approach gives a solution for those cases.
n = 61
The n = 61 case (determining an integer solution satisfying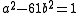), issued as a challenge by Fermat many centuries later, was given by Bhaskara as an example.We start with a solution
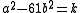for any k found by any means. In this case we can let b be 1, thus, since 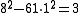, we have the triple 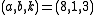. Composing it with 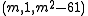gives the triple 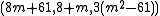, which is scaled down (or Bhaskara's lemma is directly used) to get:
For 3 to divide
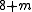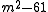and to be minimal, we choose m=7, so that we have the triple 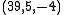. Now that k is −4, we can use Brahmagupta's idea: it can be scaled down to the rational solution 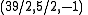, which composed with itself twice gives and then 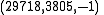. Finally, this is composed with itself, giving the solution . This is the minimal integer solution.n = 67
Suppose we are to solve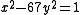 for x and y.We start with a solution
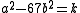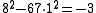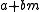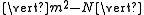for any k found by any means; in this case we can let b be 1, thus producing . At each step, we find an m > 0 such that k divides , and is minimal. We then update a, b, and k to 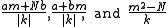respectively.First iteration
We have a = 8, b = 1, k = −3. We want a positive integer m such that k divides a+mb, i.e. 3 divides 8+m, and
is minimal. The first condition implies that m is of the form 3t+1 (i.e. 1, 4, 7, 10,… etc.), and among such m, the minimal value is attained for m=7. Replacing (a, b, k) with (am+Nb)/|k|, (a + bm)/|k|, and (m2 − N)/k, we get the new values 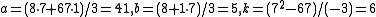. That is, we have the new solution:
At this point, one round of the cyclic algorithm is complete.
Second iteration
We now repeat the process. We have a = 41, b = 5, k = 6. We want an m > 0 such that k divides a + mb, i.e. 6 divides 41 + 5m, and |m2 − 67| is minimal. The first condition implies that m is of the form 6t + 5 (i.e. 5, 11, 17,…), and among such m, |m2 − 67| is minimal for m = 5. This leads to the new solution a = (41⋅5 + 67⋅5)/6, etc.:
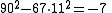
Third iteration
For 7 to divide 90+11m, we must have m = 2 + 7t (2, 9, 16,…) and among such m, we pick m=9.
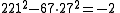
Final solution
At this point, we could continue with the cyclic method (and it would end, after seven iterations), but since the right-hand side is among ±1, ±2, ±4, we can also use Brahmagupta's observation directly. Composing the triple (221, 27, −2) with itself, we get
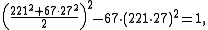
that is, we have the integer solution:
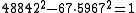
This equation approximates
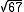(as 48842/5967) to within a margin of about .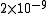