
Particular point topology
Encyclopedia
In mathematics
, the particular point topology (or included point topology) is a topology
where sets are considered open
if they are empty or contain a particular, arbitrarily chosen, point of the topological space
. Formally, let X be any set and p ∈ X. The collection
of subsets of X is then the particular point topology on X. There are a variety of cases which are individually named:
A generalization of the particular point topology is the closed extension topology
. In the case when X \ {p} has the discrete topology, the closed extension topology is the same as the particular point topology.
This topology is used to provide interesting examples and counterexamples.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the particular point topology (or included point topology) is a topology
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
where sets are considered open
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
if they are empty or contain a particular, arbitrarily chosen, point of the topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
. Formally, let X be any set and p ∈ X. The collection
- T = {S ⊆ X: p ∈ S or S = ∅}
of subsets of X is then the particular point topology on X. There are a variety of cases which are individually named:
- If X = {0,1} we call X the Sierpiński spaceSierpinski spaceIn mathematics, the Sierpiński space is a finite topological space with two points, only one of which is closed.It is the smallest example of a topological space which is neither trivial nor discrete...
. This case is somewhat special and is handled separately. - If X is finite (with at least 3 points) we call the topology on X the finite particular point topology.
- If X is countably infinite we call the topology on X the countable particular point topology.
- If X is uncountable we call the topology on X the uncountable particular point topology.
A generalization of the particular point topology is the closed extension topology
Closed extension topology
In topology, a branch of mathematics, an extension topology is a topology placed on the disjoint union of a topological space and another set.There are various types of extension topology, described in the sections below.- Extension topology :...
. In the case when X \ {p} has the discrete topology, the closed extension topology is the same as the particular point topology.
This topology is used to provide interesting examples and counterexamples.
Properties
Closed sets have empty interior- Given an open set
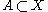 every
every 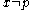 is a limit pointLimit pointIn mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
is a limit pointLimit pointIn mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
of A. So the closure of any open set other than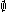 is
is 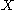 . No closed set other than
. No closed set other than 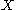 contains p so the interior of every closed set other than
contains p so the interior of every closed set other than 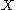 is
is 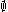 .
.
Connectedness Properties
Path and locally connected but not arc connectedConnected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
-
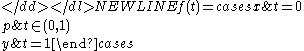
- f is a path for all x,y ∈ X. However since p is open, the preimage of p under a continuous injection from [0,1] would be an open single point of [0,1], which is a contradiction.
Dispersion point, example of a set with- p is a dispersion pointDispersion pointIn topology, a dispersion point or explosion point is a point in a topological space the removal of which leaves the space highly disconnected....
for X. That is X\{p} is totally disconnected.
Hyperconnected but not ultraconnected- Every open set contains p hence X is hyperconnected. But if a and b are in X such that p, a, and b are three distinct points, then {a} and {b} are disjoint closed sets and thus X is not ultraconnected. Note that if X is the Sierpinski space then no such a and b exist and X is in fact ultraconnected.
Compactness Properties
Closure of compact not compact- The set {p} is compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
. However its closureClosure (topology)In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
(the closure of a compact set) is the entire space X and if X is infinite this is not compact (since any set {t,p} is open). For similar reasons if X is uncountable then we have an example where the closure of a compact set is not a Lindelöf spaceLindelöf spaceIn mathematics, a Lindelöf space is a topological space in which every open cover has a countable subcover. The Lindelöf property is a weakening of the more commonly used notion of compactness, which requires the existence of a finite subcover....
.
Pseudocompact but not weakly countably compact- First there are no disjoint non-empty open sets (since all open sets contain 'p'). Hence every continuous function to the real lineReal lineIn mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
must be constant, and hence bounded, proving that X is a pseudocompact spacePseudocompact spaceIn mathematics, in the field of topology, a topological space is said to be pseudocompact if its image under any continuous function to R is bounded.-Properties related to pseudocompactness:...
. Any set not containing p does not have a limit point thus if X if infinite it is not weakly countably compact.
Locally compact but not strongly locally compact. Both possibilities regarding global compactness.- If x ∈ X then the set
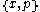 is a compact neighborhood of x. However the closure of this neighborhood is all of X and hence X is not strongly locally compact.
is a compact neighborhood of x. However the closure of this neighborhood is all of X and hence X is not strongly locally compact. - In terms of global compactness, X finite if and only if X is compact. The first implication is immediate, the reverse implication follows from noting that
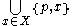 is an open cover with no finite subcover.
is an open cover with no finite subcover.
Limit related
Limit point but not an accumulation point- A sequenceSequenceIn mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
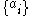 converges whenever
converges whenever 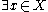 such that for all but a finite number of the
such that for all but a finite number of the 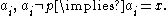 An accumulation point will be an
An accumulation point will be an 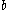 such that infinitely many of the
such that infinitely many of the 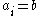 and note there may be any countable number of b's. Thus any countably infinite set of distinct points forming a sequence does not have an accumulation point but does have a limit pointLimit pointIn mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
and note there may be any countable number of b's. Thus any countably infinite set of distinct points forming a sequence does not have an accumulation point but does have a limit pointLimit pointIn mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
!
Limit point but not a ω-accumulation point- Let Y be any subset containing p. Then for any
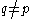 q is a limit point of Y but not a ω-accumulation point. Because this makes no use of properties of Y it leads to often cited counter examples.
q is a limit point of Y but not a ω-accumulation point. Because this makes no use of properties of Y it leads to often cited counter examples.
Separation related
T0- X is T0Kolmogorov spaceIn topology and related branches of mathematics, a topological space X is a T0 space or Kolmogorov space if for every pair of distinct points of X, at least one of them has an open neighborhood not containing the other. This condition, called the T0 condition, is one of the separation axioms...
(since {x, p} is open for each x) but satisfies no higher separation axiomSeparation axiomIn topology and related fields of mathematics, there are several restrictions that one often makes on the kinds of topological spaces that one wishes to consider. Some of these restrictions are given by the separation axioms...
s (because all open sets must contain p).
Not regular- Since every nonempty open set contains p, no closed set not containing p (such as X\{p}) can be separated by neighbourhoods from {p}, and thus X is not regularRegular spaceIn topology and related fields of mathematics, a topological space X is called a regular space if every non-empty closed subset C of X and a point p not contained in C admit non-overlapping open neighborhoods. Thus p and C...
. Since complete regularityTychonoff spaceIn topology and related branches of mathematics, Tychonoff spaces and completely regular spaces are kinds of topological spaces.These conditions are examples of separation axioms....
implies regularity, X is not completely regular.
Not normal- Since every nonempty open set contains p, no nonempty closed sets can be separated by neighbourhoods from each other, and thus X is not normalNormal spaceIn topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
. Exception: the Sierpinski topology is normal, and even completely normal, since it contains no nontrivial separated sets.
Separability- {p} is dense and hence X is a separable space. However if X is uncountableUncountable setIn mathematics, an uncountable set is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger than that of the set of all natural numbers.-Characterizations:There...
then X\{p} is not separable. This is an example of a subspace of a separable space not being separable.
Countability (first but not second)- If X is uncountable then X is first countableFirst-countable spaceIn topology, a branch of mathematics, a first-countable space is a topological space satisfying the "first axiom of countability". Specifically, a space X is said to be first-countable if each point has a countable neighbourhood basis...
but not second countableSecond-countable spaceIn topology, a second-countable space, also called a completely separable space, is a topological space satisfying the second axiom of countability. A space is said to be second-countable if its topology has a countable base...
.
Comparable ( Homeomorphic topology on the same set that is not comparable)- Let
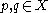 with
with 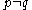 . Let
. Let 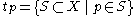 and
and 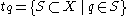 . That is tq is the particular point topology on X with q being the distinguished point. Then (X,tp) and (X,tq) are homeomorphic incomparable topologiesComparison of topologiesIn topology and related areas of mathematics comparison of topologies refers to the fact that two topological structures on a given set may stand in relation to each other. The set of all possible topologies on a given set forms a partially ordered set...
. That is tq is the particular point topology on X with q being the distinguished point. Then (X,tp) and (X,tq) are homeomorphic incomparable topologiesComparison of topologiesIn topology and related areas of mathematics comparison of topologies refers to the fact that two topological structures on a given set may stand in relation to each other. The set of all possible topologies on a given set forms a partially ordered set...
on the same set.
Density (no nonempty subsets dense in themselves)- Let S be a subset of X. If S contains p then S has no limit points (see limit point section). If S does not contain p then p is not a limit point of S. Hence S is not denseDense setIn topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
if S is nonempty.
Not first category- Any set containing p is dense in X. Hence X is not a union of nowhere dense subsetsBaire spaceIn mathematics, a Baire space is a topological space which, intuitively speaking, is very large and has "enough" points for certain limit processes. It is named in honor of René-Louis Baire who introduced the concept.- Motivation :...
.
Subspaces- Every subspace of a set given the particular point topology that doesn't contain the particular point, inherits the discrete topology.
See also
- Sierpiński spaceSierpinski spaceIn mathematics, the Sierpiński space is a finite topological space with two points, only one of which is closed.It is the smallest example of a topological space which is neither trivial nor discrete...
- Excluded point topologyExcluded point topologyIn mathematics, the excluded point topology is a topology where exclusion of a particular point defines openness. Formally, let X be any set and p ∈ X. The collectionof subsets of X is then the excluded point topology on X....
- Alexandrov topologyAlexandrov topologyIn topology, an Alexandrov space is a topological space in which the intersection of any family of open sets is open. It is an axiom of topology that the intersection of any finite family of open sets is open...
- Finite topological spaceFinite topological spaceIn mathematics, a finite topological space is a topological space for which the underlying point set is finite. That is, it is a topological space for which there are only finitely many points....
- One-point compactification

