
Excluded point topology
Encyclopedia
In mathematics
, the excluded point topology is a topology
where exclusion of a particular point defines openness
. Formally, let X be any set and p ∈ X. The collection
of subsets of X is then the excluded point topology on X.
There are a variety of cases which are individually named:
A generalization / related topology is the open extension topology. That is if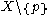 has the discrete topology then the open extension topology will be the excluded point topology.
has the discrete topology then the open extension topology will be the excluded point topology.
This topology is used to provide interesting examples and counterexamples.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the excluded point topology is a topology
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
where exclusion of a particular point defines openness
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
. Formally, let X be any set and p ∈ X. The collection
- T = {S ⊆ X: p ∉ S or S = X;}
of subsets of X is then the excluded point topology on X.
There are a variety of cases which are individually named:
- If X has two points we call it the Sierpiński spaceSierpinski spaceIn mathematics, the Sierpiński space is a finite topological space with two points, only one of which is closed.It is the smallest example of a topological space which is neither trivial nor discrete...
. This case is somewhat special and is handled separately. - If X is finite (with at least 3 points) we call the topology on X the finite excluded point topology
- If X is countably infinite we call the topology on X the countable excluded point topology
- If X is uncountable we call the topology on X the uncountable excluded point topology
A generalization / related topology is the open extension topology. That is if
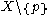 has the discrete topology then the open extension topology will be the excluded point topology.
has the discrete topology then the open extension topology will be the excluded point topology.This topology is used to provide interesting examples and counterexamples.
See also
- Sierpiński spaceSierpinski spaceIn mathematics, the Sierpiński space is a finite topological space with two points, only one of which is closed.It is the smallest example of a topological space which is neither trivial nor discrete...
- Particular point topologyParticular point topologyIn mathematics, the particular point topology is a topology where sets are considered open if they are empty or contain a particular, arbitrarily chosen, point of the topological space. Formally, let X be any set and p ∈ X. The collectionof subsets of X is then the particular point topology...
- Alexandrov topologyAlexandrov topologyIn topology, an Alexandrov space is a topological space in which the intersection of any family of open sets is open. It is an axiom of topology that the intersection of any finite family of open sets is open...
- Finite topological spaceFinite topological spaceIn mathematics, a finite topological space is a topological space for which the underlying point set is finite. That is, it is a topological space for which there are only finitely many points....
- Fort spaceFort spaceIn mathematics, Fort space, named after M. K. Fort, Jr., is an example in the theory of topological spaces.Let X be an infinite set of points, of which P is one...

