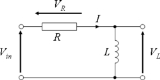
RL circuit
Overview
Infinite impulse response
Infinite impulse response is a property of signal processing systems. Systems with this property are known as IIR systems or, when dealing with filter systems, as IIR filters. IIR systems have an impulse response function that is non-zero over an infinite length of time...
electronic filter
Electronic filter
Electronic filters are electronic circuits which perform signal processing functions, specifically to remove unwanted frequency components from the signal, to enhance wanted ones, or both...
s. It consists of a resistor
Resistor
A linear resistor is a linear, passive two-terminal electrical component that implements electrical resistance as a circuit element.The current through a resistor is in direct proportion to the voltage across the resistor's terminals. Thus, the ratio of the voltage applied across a resistor's...
and an inductor
Inductor
An inductor is a passive two-terminal electrical component used to store energy in a magnetic field. An inductor's ability to store magnetic energy is measured by its inductance, in units of henries...
, either in series or in parallel, driven by a voltage source
Voltage source
In electric circuit theory, an ideal voltage source is a circuit element where the voltage across it is independent of the current through it. A voltage source is the dual of a current source. In analysis, a voltage source supplies a constant DC or AC potential between its terminals for any current...
.
The fundamental passive
Passivity (engineering)
Passivity is a property of engineering systems, used in a variety of engineering disciplines, but most commonly found in analog electronics and control systems...
linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
circuit elements are the resistor
Resistor
A linear resistor is a linear, passive two-terminal electrical component that implements electrical resistance as a circuit element.The current through a resistor is in direct proportion to the voltage across the resistor's terminals. Thus, the ratio of the voltage applied across a resistor's...
(R), capacitor
Capacitor
A capacitor is a passive two-terminal electrical component used to store energy in an electric field. The forms of practical capacitors vary widely, but all contain at least two electrical conductors separated by a dielectric ; for example, one common construction consists of metal foils separated...
(C) and inductor
Inductor
An inductor is a passive two-terminal electrical component used to store energy in a magnetic field. An inductor's ability to store magnetic energy is measured by its inductance, in units of henries...
(L). These circuit elements can be combined to form an electrical circuit in four distinct ways: the RC circuit
RC circuit
A resistor–capacitor circuit ', or RC filter or RC network, is an electric circuit composed of resistors and capacitors driven by a voltage or current source...
, the RL circuit, the LC circuit
LC circuit
An LC circuit, also called a resonant circuit or tuned circuit, consists of an inductor, represented by the letter L, and a capacitor, represented by the letter C...
and the RLC circuit
RLC circuit
An RLC circuit is an electrical circuit consisting of a resistor, an inductor, and a capacitor, connected in series or in parallel. The RLC part of the name is due to those letters being the usual electrical symbols for resistance, inductance and capacitance respectively...
with the abbreviations indicating which components are used.

