
Ewald summation
Encyclopedia
Ewald summation, named after Paul Peter Ewald
, is a method for computing the interaction energies of periodic systems (e.g. crystals), particularly electrostatic energies. Ewald summation is a special case of the Poisson summation formula
, replacing the summation of interaction energies in real space with an equivalent summation in Fourier space. The advantage of this approach is the rapid convergence of the Fourier-space summation compared to its real-space equivalent when the real-space interactions are long-range. Because electrostatic energies consist of both short- and long-range interactions, it is maximally efficient to decompose the interaction potential into a short-range component summed in real space and a long-range component summed in Fourier space.
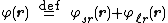
where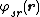 represents the short-range term that sums quickly in real space and
represents the short-range term that sums quickly in real space and 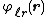 represents the long-range term that sums quickly in Fourier space. The long-ranged part should be finite for all arguments (most notably r = 0) but may have any convenient mathematical form, most typically a Gaussian distribution. The method assumes that the short-range part can be summed easily; hence, the problem becomes the summation of the long-range term. Due to the use of the Fourier sum, the method implicitly assumes that the system under study is infinitely periodic (a sensible assumption for the interiors of crystals). One repeating unit of this hypothetical periodic system is called a unit cell. One such cell is chosen as the "central cell" for reference and the remaining cells are called images.
represents the long-range term that sums quickly in Fourier space. The long-ranged part should be finite for all arguments (most notably r = 0) but may have any convenient mathematical form, most typically a Gaussian distribution. The method assumes that the short-range part can be summed easily; hence, the problem becomes the summation of the long-range term. Due to the use of the Fourier sum, the method implicitly assumes that the system under study is infinitely periodic (a sensible assumption for the interiors of crystals). One repeating unit of this hypothetical periodic system is called a unit cell. One such cell is chosen as the "central cell" for reference and the remaining cells are called images.
The long-range interaction energy is the sum of interaction energies between the charges of a central unit cell and all the charges of the lattice. Hence, it can be represented as a double integral over two charge density fields representing the fields of the unit cell and the crystal lattice

where the unit-cell charge density field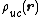 is a sum over the positions
is a sum over the positions 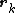 of the charges
of the charges 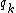 in the central unit cell
in the central unit cell
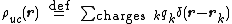
and the total charge density field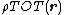 is the same sum over the unit-cell charges
is the same sum over the unit-cell charges  and their periodic images
and their periodic images
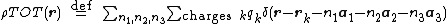
Here,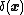 is the Dirac delta function
is the Dirac delta function
,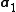 ,
,  and
and 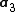 are the lattice vectors and
are the lattice vectors and  ,
, 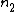 and
and 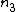 range over all integers. The total field
range over all integers. The total field 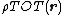 can be represented as a convolution
can be represented as a convolution
of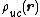 with a lattice function
with a lattice function 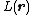
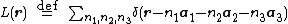
Since this is a convolution
, the Fourier transformation of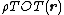 is a product
is a product
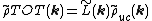
where the Fourier transform of the lattice function is another sum over delta functions

where the reciprocal space vectors are defined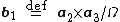 (and cyclic permutations) where
(and cyclic permutations) where 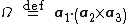 is the volume of the central unit cell (if it is geometrically a parallelepiped
is the volume of the central unit cell (if it is geometrically a parallelepiped
, which is often but not necessarily the case). Note that both and
and 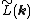 are real, even functions.
are real, even functions.
For brevity, define an effective single-particle potential
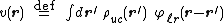
Since this is also a convolution, the Fourier transformation of the same equation is a product
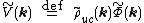
where the Fourier transform is defined
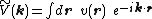
The energy can now be written as a single field integral
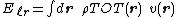
Using Parseval's theorem
, the energy can also be summed in Fourier space
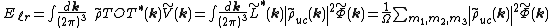
where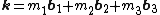
in the final summation.
This is the essential result. Once is calculated, the summation/integration over
is calculated, the summation/integration over  is straightforward and should converge quickly. The most common reason for lack of convergence is a poorly defined unit cell, which must be charge neutral to avoid infinite sums.
is straightforward and should converge quickly. The most common reason for lack of convergence is a poorly defined unit cell, which must be charge neutral to avoid infinite sums.
, long before the advent of computer
s. However, the Ewald method has enjoyed widespread use since the 1970s in computer simulation
s of particle systems, especially those interacting via an inverse square force
law such as gravity or electrostatics
. Applications include simulations of plasma
s, galaxies
and molecules.
As in normal Ewald summation, a generic interaction potential is separated into two terms
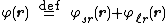 - a short-ranged part
- a short-ranged part  that sums quickly in real space and a long-ranged part
that sums quickly in real space and a long-ranged part  that sums quickly in Fourier space. The basic idea of particle mesh Ewald summation is to replace the direct summation of interaction energies between point particles
that sums quickly in Fourier space. The basic idea of particle mesh Ewald summation is to replace the direct summation of interaction energies between point particles

with two summations, a direct sum of the short-ranged potential in real space
of the short-ranged potential in real space

(that is the particle part of particle mesh Ewald) and a summation in Fourier space of the long-ranged
part
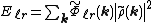
where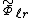 and
and 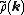 represent the Fourier transform
represent the Fourier transform
s of the potential
and the charge density
(that's the Ewald part). Since both summations converge quickly in their respective spaces (real and Fourier), they may be truncated with little loss of accuracy and great improvement in required computational time. To evaluate the Fourier transform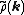 of the charge density field efficiently, one uses the Fast Fourier transform
of the charge density field efficiently, one uses the Fast Fourier transform
, which requires that the density field be evaluated on a discrete lattice in space (that's the mesh part).
Due to the periodicity assumption implicit in Ewald summation, applications of the PME method to physical systems require the imposition of periodic symmetry. Thus, the method is best suited to systems that can be simulated as infinite in spatial extent. In molecular dynamics
simulations this is normally accomplished by deliberately constructing a charge-neutral unit cell that can be infinitely "tiled" to form images; however, to properly account for the effects of this approximation, these images are reincorporated back into the original simulation cell. The overall effect is called a periodic boundary condition
. To visualize this most clearly, think of a unit cube; the upper face is effectively in contact with the lower face, the right with the left face, and the front with the back face. As a result the unit cell size must be carefully chosen to be large enough to avoid improper motion correlations between two faces "in contact", but still small enough to be computationally feasible. The definition of the cutoff between short- and long-range interactions can also introduce artifacts.
The restriction of the density field to a mesh makes the PME method more efficient for systems with "smooth" variations in density, or continuous potential functions. Localized systems or those with large fluctuations in density may be treated more efficiently with the fast multipole method of Greengard and Rokhlin.
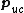 in the unit cell) is conditionally convergent, i.e., depends on the order of the summation. For example, if the dipole-dipole interactions of a central unit cell with unit cells located on an ever-increasing cube, the energy converges to a different value than if the interaction energies had been summed spherically. Roughly speaking, this conditional convergence arises because (1) the number of interacting dipoles on a shell of radius
in the unit cell) is conditionally convergent, i.e., depends on the order of the summation. For example, if the dipole-dipole interactions of a central unit cell with unit cells located on an ever-increasing cube, the energy converges to a different value than if the interaction energies had been summed spherically. Roughly speaking, this conditional convergence arises because (1) the number of interacting dipoles on a shell of radius  grows like
grows like  ; (2) the strength of a single dipole-dipole interaction falls like
; (2) the strength of a single dipole-dipole interaction falls like 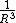 ; and (3) the mathematical summation
; and (3) the mathematical summation  diverges.
diverges.
This somewhat surprising result can be reconciled with the finite energy of real crystals because such crystals are not infinite, i.e., have a particular boundary. More specifically, the boundary of a polar
crystal has an effective surface charge density on its surface where
where  is the surface normal vector and
is the surface normal vector and 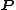 represents the net dipole moment per volume. The interaction energy
represents the net dipole moment per volume. The interaction energy  of the dipole in a central unit cell with that surface charge density can be written
of the dipole in a central unit cell with that surface charge density can be written

where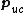 and
and  are the net dipole moment and volume of the unit cell,
are the net dipole moment and volume of the unit cell, 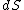 is an infinitesimal area on the crystal surface and
is an infinitesimal area on the crystal surface and 
is the vector from the central unit cell to the infinitesimal area. This formula results from integrating the energy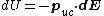 where
where 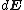 represents the infinitesimal electric field generated by an infinitesimal surface charge
represents the infinitesimal electric field generated by an infinitesimal surface charge 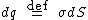 (Coulomb's law
(Coulomb's law
)
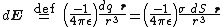
The negative sign derives from the definition of , which points towards the charge, not away from it.
, which points towards the charge, not away from it.
in 1921 (see References below) to determine the electrostatic energy (and, hence, the Madelung constant
) of ionic crystals.
. Direct calculation gives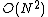 , where
, where 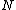 is the number of atoms in the system. The PME method gives
is the number of atoms in the system. The PME method gives 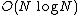 .
.
Paul Peter Ewald
Paul Peter Ewald was a German-born U.S. crystallographer and physicist, a pioneer of X-ray diffraction methods.-Education:...
, is a method for computing the interaction energies of periodic systems (e.g. crystals), particularly electrostatic energies. Ewald summation is a special case of the Poisson summation formula
Poisson summation formula
In mathematics, the Poisson summation formula is an equation that relates the Fourier series coefficients of the periodic summation of a function to values of the function's continuous Fourier transform. Consequently, the periodic summation of a function is completely defined by discrete samples...
, replacing the summation of interaction energies in real space with an equivalent summation in Fourier space. The advantage of this approach is the rapid convergence of the Fourier-space summation compared to its real-space equivalent when the real-space interactions are long-range. Because electrostatic energies consist of both short- and long-range interactions, it is maximally efficient to decompose the interaction potential into a short-range component summed in real space and a long-range component summed in Fourier space.
Derivation
Ewald summation rewrites the interaction potential as the sum of two terms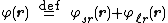
where
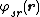 represents the short-range term that sums quickly in real space and
represents the short-range term that sums quickly in real space and 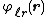 represents the long-range term that sums quickly in Fourier space. The long-ranged part should be finite for all arguments (most notably r = 0) but may have any convenient mathematical form, most typically a Gaussian distribution. The method assumes that the short-range part can be summed easily; hence, the problem becomes the summation of the long-range term. Due to the use of the Fourier sum, the method implicitly assumes that the system under study is infinitely periodic (a sensible assumption for the interiors of crystals). One repeating unit of this hypothetical periodic system is called a unit cell. One such cell is chosen as the "central cell" for reference and the remaining cells are called images.
represents the long-range term that sums quickly in Fourier space. The long-ranged part should be finite for all arguments (most notably r = 0) but may have any convenient mathematical form, most typically a Gaussian distribution. The method assumes that the short-range part can be summed easily; hence, the problem becomes the summation of the long-range term. Due to the use of the Fourier sum, the method implicitly assumes that the system under study is infinitely periodic (a sensible assumption for the interiors of crystals). One repeating unit of this hypothetical periodic system is called a unit cell. One such cell is chosen as the "central cell" for reference and the remaining cells are called images.The long-range interaction energy is the sum of interaction energies between the charges of a central unit cell and all the charges of the lattice. Hence, it can be represented as a double integral over two charge density fields representing the fields of the unit cell and the crystal lattice

where the unit-cell charge density field
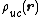 is a sum over the positions
is a sum over the positions 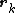 of the charges
of the charges 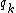 in the central unit cell
in the central unit cell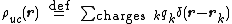
and the total charge density field
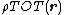 is the same sum over the unit-cell charges
is the same sum over the unit-cell charges  and their periodic images
and their periodic images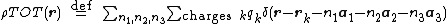
Here,
 is the Dirac delta function
is the Dirac delta functionDirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
,
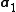 ,
,  and
and 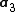 are the lattice vectors and
are the lattice vectors and  ,
, 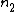 and
and 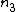 range over all integers. The total field
range over all integers. The total field 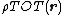 can be represented as a convolution
can be represented as a convolutionConvolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
of
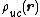 with a lattice function
with a lattice function 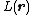
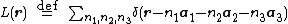
Since this is a convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
, the Fourier transformation of
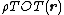 is a product
is a product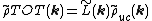
where the Fourier transform of the lattice function is another sum over delta functions

where the reciprocal space vectors are defined
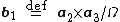 (and cyclic permutations) where
(and cyclic permutations) where 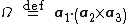 is the volume of the central unit cell (if it is geometrically a parallelepiped
is the volume of the central unit cell (if it is geometrically a parallelepipedParallelepiped
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, its definition encompasses all four concepts...
, which is often but not necessarily the case). Note that both
 and
and 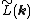 are real, even functions.
are real, even functions.For brevity, define an effective single-particle potential
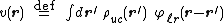
Since this is also a convolution, the Fourier transformation of the same equation is a product
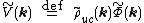
where the Fourier transform is defined
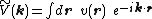
The energy can now be written as a single field integral
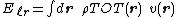
Using Parseval's theorem
Parseval's theorem
In mathematics, Parseval's theorem usually refers to the result that the Fourier transform is unitary; loosely, that the sum of the square of a function is equal to the sum of the square of its transform. It originates from a 1799 theorem about series by Marc-Antoine Parseval, which was later...
, the energy can also be summed in Fourier space
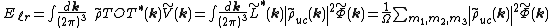
where
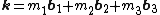
in the final summation.
This is the essential result. Once
 is calculated, the summation/integration over
is calculated, the summation/integration over  is straightforward and should converge quickly. The most common reason for lack of convergence is a poorly defined unit cell, which must be charge neutral to avoid infinite sums.
is straightforward and should converge quickly. The most common reason for lack of convergence is a poorly defined unit cell, which must be charge neutral to avoid infinite sums.Particle mesh Ewald (PME) method
Ewald summation was developed as a method of theoretical physicsTheoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, long before the advent of computer
Computer
A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
s. However, the Ewald method has enjoyed widespread use since the 1970s in computer simulation
Computer simulation
A computer simulation, a computer model, or a computational model is a computer program, or network of computers, that attempts to simulate an abstract model of a particular system...
s of particle systems, especially those interacting via an inverse square force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
law such as gravity or electrostatics
Electrostatics
Electrostatics is the branch of physics that deals with the phenomena and properties of stationary or slow-moving electric charges....
. Applications include simulations of plasma
Plasma (physics)
In physics and chemistry, plasma is a state of matter similar to gas in which a certain portion of the particles are ionized. Heating a gas may ionize its molecules or atoms , thus turning it into a plasma, which contains charged particles: positive ions and negative electrons or ions...
s, galaxies
Galaxy
A galaxy is a massive, gravitationally bound system that consists of stars and stellar remnants, an interstellar medium of gas and dust, and an important but poorly understood component tentatively dubbed dark matter. The word galaxy is derived from the Greek galaxias , literally "milky", a...
and molecules.
As in normal Ewald summation, a generic interaction potential is separated into two terms
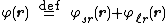 - a short-ranged part
- a short-ranged part  that sums quickly in real space and a long-ranged part
that sums quickly in real space and a long-ranged part  that sums quickly in Fourier space. The basic idea of particle mesh Ewald summation is to replace the direct summation of interaction energies between point particles
that sums quickly in Fourier space. The basic idea of particle mesh Ewald summation is to replace the direct summation of interaction energies between point particles
with two summations, a direct sum
 of the short-ranged potential in real space
of the short-ranged potential in real space
(that is the particle part of particle mesh Ewald) and a summation in Fourier space of the long-ranged
part
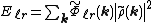
where
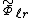 and
and 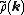 represent the Fourier transform
represent the Fourier transformFourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
s of the potential
Potential
*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...
and the charge density
Charge density
The linear, surface, or volume charge density is the amount of electric charge in a line, surface, or volume, respectively. It is measured in coulombs per meter , square meter , or cubic meter , respectively, and represented by the lowercase Greek letter Rho . Since there are positive as well as...
(that's the Ewald part). Since both summations converge quickly in their respective spaces (real and Fourier), they may be truncated with little loss of accuracy and great improvement in required computational time. To evaluate the Fourier transform
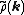 of the charge density field efficiently, one uses the Fast Fourier transform
of the charge density field efficiently, one uses the Fast Fourier transformFast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
, which requires that the density field be evaluated on a discrete lattice in space (that's the mesh part).
Due to the periodicity assumption implicit in Ewald summation, applications of the PME method to physical systems require the imposition of periodic symmetry. Thus, the method is best suited to systems that can be simulated as infinite in spatial extent. In molecular dynamics
Molecular dynamics
Molecular dynamics is a computer simulation of physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a period of time, giving a view of the motion of the atoms...
simulations this is normally accomplished by deliberately constructing a charge-neutral unit cell that can be infinitely "tiled" to form images; however, to properly account for the effects of this approximation, these images are reincorporated back into the original simulation cell. The overall effect is called a periodic boundary condition
Periodic boundary conditions
In mathematical models and computer simulations, periodic boundary conditions are a set of boundary conditions that are often used to simulate a large system by modelling a small part that is far from its edge...
. To visualize this most clearly, think of a unit cube; the upper face is effectively in contact with the lower face, the right with the left face, and the front with the back face. As a result the unit cell size must be carefully chosen to be large enough to avoid improper motion correlations between two faces "in contact", but still small enough to be computationally feasible. The definition of the cutoff between short- and long-range interactions can also introduce artifacts.
The restriction of the density field to a mesh makes the PME method more efficient for systems with "smooth" variations in density, or continuous potential functions. Localized systems or those with large fluctuations in density may be treated more efficiently with the fast multipole method of Greengard and Rokhlin.
Dipole term
The electrostatic energy of a polar crystal (i.e., a crystal with a net dipole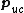 in the unit cell) is conditionally convergent, i.e., depends on the order of the summation. For example, if the dipole-dipole interactions of a central unit cell with unit cells located on an ever-increasing cube, the energy converges to a different value than if the interaction energies had been summed spherically. Roughly speaking, this conditional convergence arises because (1) the number of interacting dipoles on a shell of radius
in the unit cell) is conditionally convergent, i.e., depends on the order of the summation. For example, if the dipole-dipole interactions of a central unit cell with unit cells located on an ever-increasing cube, the energy converges to a different value than if the interaction energies had been summed spherically. Roughly speaking, this conditional convergence arises because (1) the number of interacting dipoles on a shell of radius  grows like
grows like  ; (2) the strength of a single dipole-dipole interaction falls like
; (2) the strength of a single dipole-dipole interaction falls like 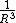 ; and (3) the mathematical summation
; and (3) the mathematical summation  diverges.
diverges.This somewhat surprising result can be reconciled with the finite energy of real crystals because such crystals are not infinite, i.e., have a particular boundary. More specifically, the boundary of a polar
crystal has an effective surface charge density on its surface
 where
where  is the surface normal vector and
is the surface normal vector and 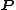 represents the net dipole moment per volume. The interaction energy
represents the net dipole moment per volume. The interaction energy  of the dipole in a central unit cell with that surface charge density can be written
of the dipole in a central unit cell with that surface charge density can be written
where
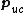 and
and  are the net dipole moment and volume of the unit cell,
are the net dipole moment and volume of the unit cell, 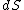 is an infinitesimal area on the crystal surface and
is an infinitesimal area on the crystal surface and 
is the vector from the central unit cell to the infinitesimal area. This formula results from integrating the energy
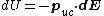 where
where 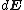 represents the infinitesimal electric field generated by an infinitesimal surface charge
represents the infinitesimal electric field generated by an infinitesimal surface charge 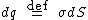 (Coulomb's law
(Coulomb's lawCoulomb's law
Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
)
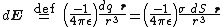
The negative sign derives from the definition of
 , which points towards the charge, not away from it.
, which points towards the charge, not away from it.History
The Ewald summation was developed by Paul Peter EwaldPaul Peter Ewald
Paul Peter Ewald was a German-born U.S. crystallographer and physicist, a pioneer of X-ray diffraction methods.-Education:...
in 1921 (see References below) to determine the electrostatic energy (and, hence, the Madelung constant
Madelung constant
The Madelung constant is used in determining the electrostatic potential of a single ion in a crystal by approximating the ions by point charges. It is named after Erwin Madelung, a German physicist....
) of ionic crystals.
Scaling
Generally different Ewald summation methods give different time complexitiesTime complexity
In computer science, the time complexity of an algorithm quantifies the amount of time taken by an algorithm to run as a function of the size of the input to the problem. The time complexity of an algorithm is commonly expressed using big O notation, which suppresses multiplicative constants and...
. Direct calculation gives
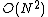 , where
, where 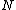 is the number of atoms in the system. The PME method gives
is the number of atoms in the system. The PME method gives 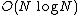 .
.See also
- Paul Peter EwaldPaul Peter EwaldPaul Peter Ewald was a German-born U.S. crystallographer and physicist, a pioneer of X-ray diffraction methods.-Education:...
- Madelung constantMadelung constantThe Madelung constant is used in determining the electrostatic potential of a single ion in a crystal by approximating the ions by point charges. It is named after Erwin Madelung, a German physicist....
- Poisson summation formulaPoisson summation formulaIn mathematics, the Poisson summation formula is an equation that relates the Fourier series coefficients of the periodic summation of a function to values of the function's continuous Fourier transform. Consequently, the periodic summation of a function is completely defined by discrete samples...
- Molecular modeling

