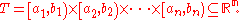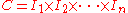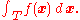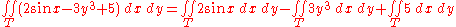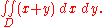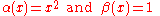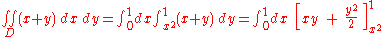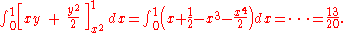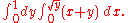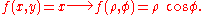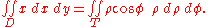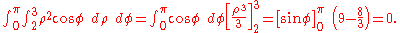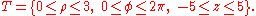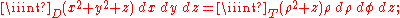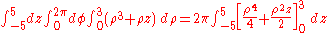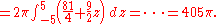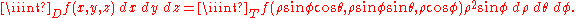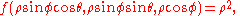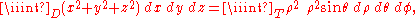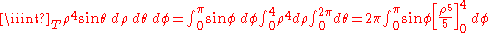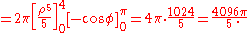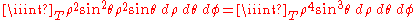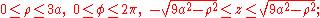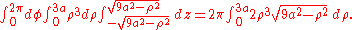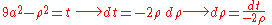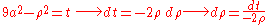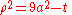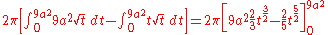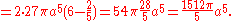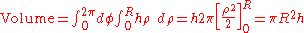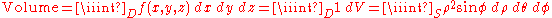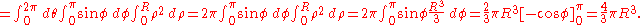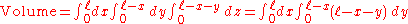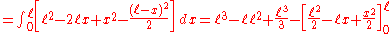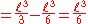Multiple integral
Encyclopedia

Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
extended to functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of more than one real variable
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
, for example, ƒ(x, y) or ƒ(x, y, z). Integrals of a function of two variables over a region in ℝ2 are called double integrals.
Introduction
Just as the definite integral of a positive function of one variable represents the areaArea
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
of the region between the graph of the function and the x-axis, the double integral of a positive function of two variables represents the volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
of the region between the surface defined by the function (on the three dimensional Cartesian plane where z = ƒ(x, y)) and the plane which contains its domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
. (Note that the same volume can be obtained via the triple integral—the integral of a function in three variables—of the constant function ƒ(x, y, z) = 1 over the above-mentioned region between the surface and the plane.) If there are more variables, a multiple integral will yield hypervolumes of multi-dimensional functions.
Multiple integration of a function in n variables: f(x1, x2, ..., xn) over a domain D is most commonly represented by nested integral signs in the reverse order of execution (the leftmost integral sign is computed last), followed by the function and integrand arguments in proper order (the integral with respect to the rightmost argument is computed last). The domain of integration is either represented symbolically for every argument over each integral sign, or is abbreviated by a variable at the rightmost integral sign:

Since the concept of an antiderivative
Antiderivative
In calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...
is only defined for functions of a single real variable, the usual definition of the indefinite integral does not immediately extend to the multiple integral.
Mathematical definition
For n > 1, consider a so-called "half-open" n-dimensional hyperrectangularHyperrectangle
In geometry, an orthotope is the generalization of a rectangle for higher dimensions, formally defined as the Cartesian product of intervals....
domain T, defined as:
Partition each interval [aj, bj) into a finite family Ij of non-overlapping subintervals ijα , with each subinterval closed at the left end, and open at the right end.
Then the finite family of subrectangles C given by
is a partition of T; that is, the subrectangles Ck are non-overlapping and their union is T.
Let f : T → R be a function defined on T. Consider a partition C of T as defined above, such that C is a family of m subrectangles Cm and
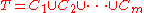
We can approximate the total nth-dimensional volume bounded below by T and above by f with the following Riemann sum
Riemann sum
In mathematics, a Riemann sum is a method for approximating the total area underneath a curve on a graph, otherwise known as an integral. It mayalso be used to define the integration operation. The method was named after German mathematician Bernhard Riemann....
:
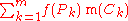
where Pk is a point in Ck and m(Ck) is the product of the lengths of the intervals whose Cartesian product is Ck, otherwise known as the measure of Ck.
The diameter of a subrectangle Ck is the largest of the lengths of the intervals whose Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
is Ck. The diameter of a given partition of T is defined as the largest of the diameters of the subrectangles in the partition. Intuitively, as the diameter of the partition C is restricted smaller and smaller, the number of subrectangles m gets larger, and the measure m(Ck) of each subrectangle grows smaller. The function f is said to be Riemann integrable if the limit
Limit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
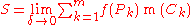
exists, where the limit is taken over all possible partitions of T of diameter at most δ.
If f is Riemann integrable, S is called the Riemann integral of f over T and is denoted

Frequently this notation is abbreviated as
where x represents the n-tuple (x1, ... xn) and dx is the n-dimensional volume differential.
The Riemann integral of a function defined over an arbitrary bounded n-dimensional set can be defined by extending that function to a function defined over a half-open rectangle whose values are zero outside the domain of the original function. Then the integral of the original function over the original domain is defined to be the integral of the extended function over its rectangular domain, if it exists.
In what follows the Riemann integral in n dimensions will be called multiple integral.
Properties
Multiple integrals have many properties common to those of integrals of functions of one variable (linearity, commutativity, monotonicity, and so on.). One important property of multiple integrals is that the value of an integral is independent of the order of integrands under certain conditions. This property is popularly known as Fubini's theoremFubini's theorem
In mathematical analysis Fubini's theorem, named after Guido Fubini, is a result which gives conditions under which it is possible to compute a double integral using iterated integrals. As a consequence it allows the order of integration to be changed in iterated integrals.-Theorem...
.
Particular cases
In the case of T ⊆ R2, the integral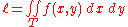
is the double integral of f on T, and if T ⊆ R3 the integral

is the triple integral of f on T.
Notice that, by convention, the double integral has two integral signs, and the triple integral has three; this is a notational convention which is convenient when computing a multiple integral as an iterated integral, as shown later in this article.
Methods of integration
The resolution of problems with multiple integrals consists, in most of cases, of finding a way to reduce the multiple integral to an iterated integralIterated integral
In calculus an iterated integral is the result of applying integrals to a function of more than one variable in a way that each of the integrals considers some of the variables as given constants. For example, the function f, if y is considered a given parameter can be integrated with respect to...
, a series of integrals of one variable, each being directly solvable. Sometimes, it is possible to obtain the result of the integration by direct examination without any calculations.
Integrating constant functions
When the integrand is a constant functionConstant function
In mathematics, a constant function is a function whose values do not vary and thus are constant. For example the function f = 4 is constant since f maps any value to 4...
c, the integral is equal to the product of c and the measure of the domain of integration. If c = 1 and the domain is a subregion of R2, the integral gives the area of the region, while if the domain is a subregion of R3, the integral gives the volume of the region.
- For example:
-
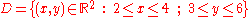 and
and 
in which case
-
 ,
,
since
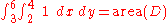 by definition.
by definition.Use of symmetry
When the domain of integration is symmetric about the origin with respect to at least one of the variables of integration and the integrand is oddEven and odd functions
In mathematics, even functions and odd functions are functions which satisfy particular symmetry relations, with respect to taking additive inverses. They are important in many areas of mathematical analysis, especially the theory of power series and Fourier series...
with respect to this variable, the integral is equal to zero, as the integrals over the two halves of the domain have the same absolute value but opposite signs. When the integrand is even
Even and odd functions
In mathematics, even functions and odd functions are functions which satisfy particular symmetry relations, with respect to taking additive inverses. They are important in many areas of mathematical analysis, especially the theory of power series and Fourier series...
with respect to this variable, the integral is equal to twice the integral over one half of the domain, as the integrals over the two halves of the domain are equal.
- Example (1):
- Consider the function
 integrated over the domain
integrated over the domain 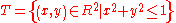 , a disc with radiusRadiusIn classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
, a disc with radiusRadiusIn classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
1 centered at the origin with the boundary included.
- Using the linearity property, the integral can be decomposed into three pieces:
- 2 sin x and 3y3 are both odd functions and moreover it is evident that the T disc has a symmetry for the x and even the y axis; therefore the only contribution to the final result of the integrals is that of the constant function 5 because the other two pieces are null.
- Example (2):
- Consider the function f(x, y, z) = x exp(y2 + z2) and as integration region the sphereSphereA sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
with radius 2 centered at the origin of the axes T = x2 + y2 + z2 ≤ 4. The "ball" is symmetric about all three axes, but it is sufficient to integrate with respect to x-axis to show that the integral is 0, because the function is an odd function of that variable.
Normal domains on R2
This method is applicable to any domain D for which:- the projection of D onto either the x-axis or the y-axis is bounded by the two values, a and b
- any line perpendicular to this axis that passes between these two values intersects the domain in an interval whose endpoints are given by the graphs of two functions,
 and
and  .
.
x-axis
If the domain D is normal with respect to the x-axis, and is a continuous function
is a continuous functionContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
; then α(x) and β(x) (defined on the interval [a, b]) are the two functions that determine D. Then:
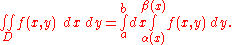
y-axis
If D is normal with respect to the y-axis and is a continuous function; then α(y) and β(y) (defined on the interval [a, b]) are the two functions that determine D. Then:
is a continuous function; then α(y) and β(y) (defined on the interval [a, b]) are the two functions that determine D. Then: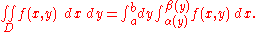
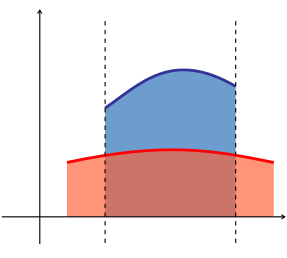
Example
- Consider this region:
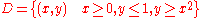 (please see the graphic in the example). Calculate
(please see the graphic in the example). Calculate
- This domain is normal with respect to both the x- and y-axes. To apply the formulae it is required to find the functions that determine D and the intervals over which these are defined.
- In this case the two functions are:
- while the interval is given by the intersections of the functions with x = 0, so the interval is [a, b] = [0, 1] (normality has been chosen with respect to the x-axis for a better visual understanding).
- It is now possible to apply the formula:
. The remaining operations consist of applying the basic techniques of integration:
- If we choose normality with respect to the y-axis we could calculate
- and obtain the same value.
Normal domains on R3
The extension of these formulae to triple integrals should be apparent:if T is a domain that is normal with respect to the xy-plane and determined by the functions α (x,y) and β(x,y), then
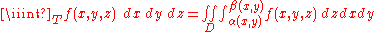
(this definition is the same for the other five normality cases on R3).
Change of variables
The limits of integration are often not easily interchangeable (without normality or with complex formulae to integrate). One makes a change of variablesChange of variables
In mathematics, a change of variables is a basic technique used to simplify problems in which the original variables are replaced with new ones; the new and old variables being related in some specified way...
to rewrite the integral in a more "comfortable" region, which can be described in simpler formulae. To do so, the function must be adapted to the new coordinates.
- Example (1-a):
- The function is
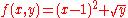 ;
; - if one adopts this substitution
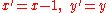 therefore
therefore 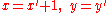
- one obtains the new function
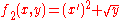 .
.
- Similarly for the domain because it is delimited by the original variables that were transformed before (x and y in example).
- the differentials dx and dy transform via the absolute value of the determinant of the Jacobian matrix containing the partial derivatives of the transformations regarding the new variable (consider, as an example, the differential transformation in polar coordinates).
- The function is
There exist three main "kinds" of changes of variable (one in R2, two in R3); however, more general substitutions can be made using the same principle.
Polar coordinates
In R2 if the domain has a circular "symmetry" and the function has some "particular" characteristics you can apply the transformation to polar coordinates (see the example in the picture) which means that the generic points P(x,y) in Cartesian coordinates switch to their respective points in polar coordinates. That allows one to change the "shape" of the domain and simplify the operations.The fundamental relation to make the transformation is the following:

Example (2-a):
- The function is
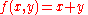
- and applying the transformation one obtains
Example (2-b):
- The function is
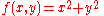
- In this case one has:
- using the Pythagorean trigonometric identityPythagorean trigonometric identityThe Pythagorean trigonometric identity is a trigonometric identity expressing the Pythagorean theorem in terms of trigonometric functions. Along with the sum-of-angles formulae, it is one the basic relations between the sine and cosine functions, from which all others may be derived.-Statement of...
(very useful to simplify this operation).
The transformation of the domain is made by defining the radius' crown length and the amplitude of the described angle to define the ρ, φ intervals starting from x, y.
Example (2-c):
- The domain is
 , that is a circumference of radius 2; it's evident that the covered angle is the circle angle, so φ varies from 0 to 2π, while the crown radius varies from 0 to 2 (the crown with the inside radius null is just a circle).
, that is a circumference of radius 2; it's evident that the covered angle is the circle angle, so φ varies from 0 to 2π, while the crown radius varies from 0 to 2 (the crown with the inside radius null is just a circle).
Example (2-d):
- The domain is
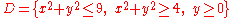 , that is the circular crown in the positive y half-plane (please see the picture in the example); note that φ describes a plane angle while ρ varies from 2 to 3. Therefore the transformed domain will be the following rectangleRectangleIn Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...
, that is the circular crown in the positive y half-plane (please see the picture in the example); note that φ describes a plane angle while ρ varies from 2 to 3. Therefore the transformed domain will be the following rectangleRectangleIn Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...
:
The Jacobian determinant of that transformation is the following:
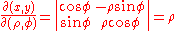
which has been obtained by inserting the partial derivatives of x = ρ cos(φ), y = ρ sin(φ) in the first column respect to ρ and in the second respect to φ, so the dx dy differentials in this transformation becomes ρ dρ dφ.
Once the function is transformed and the domain evaluated, it is possible to define the formula for the change of variables in polar coordinates:
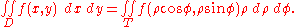
Please note that φ is valid in the [0, 2π] interval while ρ, which is a measure of a length, can only have positive values.
Example (2-e):
- The function is ƒ(x, y) = x and as the domain the same in 2-d example.
- From the previous analysis of D we know the intervals of ρ (from 2 to 3) and of φ (from 0 to π). Now let's change the function:
- finally let's apply the integration formula:
- Once the intervals are known, you have
Cylindrical coordinates
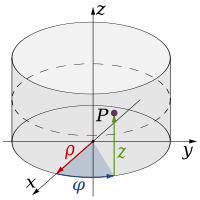
Cylindrical coordinate system
A cylindrical coordinate system is a three-dimensional coordinate systemthat specifies point positions by the distance from a chosen reference axis, the direction from the axis relative to a chosen reference direction, and the distance from a chosen reference plane perpendicular to the axis...
; the transformation of the function is made by the following relation:
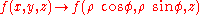
The domain transformation can be graphically attained, because only the shape of the base varies, while the height follows the shape of the starting region.
Example (3-a):
- The region is
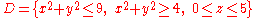 (that is the "tube" whose base is the circular crown of the 2-d example and whose height is 5); if the transformation is applied, this region is obtained:
(that is the "tube" whose base is the circular crown of the 2-d example and whose height is 5); if the transformation is applied, this region is obtained: 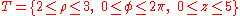 (that is the parallelepiped whose base is similar to the rectangle in 2-d example and whose height is 5).
(that is the parallelepiped whose base is similar to the rectangle in 2-d example and whose height is 5).
Because the z component is unvaried during the transformation, the dx dy dz differentials vary as in the passage in polar coordinates: therefore, they become ρ dρ dφ dz.
Finally, it is possible to apply the final formula to cylindrical coordinates:

This method is convenient in case of cylindrical or conical domains or in regions where it is easy to individuate the z interval and even transform the circular base and the function.
Example (3-b):
- The function is
 and as integration domain this cylinderCylinder (geometry)A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...
and as integration domain this cylinderCylinder (geometry)A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...
: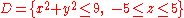 .
. - The transformation of D in cylindrical coordinates is the following:
- while the function becomes
- Finally one can apply the integration formula:
- developing the formula you have
Spherical coordinates
.svg.png)
Spherical coordinate system
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its inclination angle measured from a fixed zenith direction, and the azimuth angle of...
; the function is transformed by this relation:

Note that points on z axis do not have a precise characterization in spherical coordinates, so
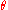 can vary between 0 to 2π .
can vary between 0 to 2π .The better integration domain for this passage is obviously the sphere.
Example (4-a):
- The domain is
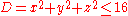 (sphere with radius 4 and center in the origin); applying the transformation you get this region:
(sphere with radius 4 and center in the origin); applying the transformation you get this region: 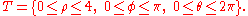
- The Jacobian determinant of this transformation is the following:
-

- The dx dy dz differentials therefore are transformed to ρ2 sin(φ) dρ dθ dφ.
- Finally you obtain the final integration formula:
- It's better to use this method in case of spherical domains and in case of functions that can be easily simplified, by the first fundamental relation of trigonometry, extended in R3 (please see example 4-b); in other cases it can be better to use cylindrical coordinates (please see example 4-c).
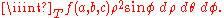
Note that the extra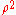 and
and  come from the Jacobian.
come from the Jacobian.
Note that in the following examples the roles of φ and θ have been reversed.
Example (4-b):
- D is the same region of the 4-a example and
 is the function to integrate.
is the function to integrate.
- Its transformation is very easy:
- while we know the intervals of the transformed region T from D:
- Let's therefore apply the integration's formula:
- and, developing, we get
Example (4-c):- The domain D is the ball with center in the origin and radius 3a (
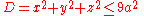 ) and
) and 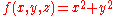 is the function to integrate.
is the function to integrate.
- Looking at the domain, it seems convenient to adopt the passage in spherical coordinates, in fact, the intervals of the variables that delimit the new T region are obviously:
- However, applying the transformation, we get
-
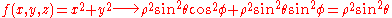 .
.
- Applying the formula for integration we would obtain:
- which is very hard to solve. This problem will be solved by using the passage in cylindrical coordinates. The new T intervals are
- the z interval has been obtained by dividing the ball in two hemispheres simply by solving the inequality from the formula of D (and then directly transforming x2 + y2 in ρ2). The new function is simply ρ2. Applying the integration formula
-
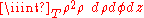 .
.
- Then we get
- Now let's apply the transformation
. We get
- because
 , we get
, we get
- after inverting the integration's bounds and multiplying the terms between parenthesis, it is possible to decompose the integral in two parts that can be directly solved:
- Thanks to the passage in cylindrical coordinates it was possible to reduce the triple integral to an easier one-variable integral.
See also the differential volume entry in nabla in cylindrical and spherical coordinates.
Double integral
Let us assume that we wish to integrate a multivariable function f over a region A.
From this we formulate the double integral
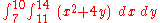
The inner integral is performed first, integrating with respect to x and taking y as a constant, as it is not the variable of integration. The result of this integral, which is a function depending only on y, is then integrated with respect to y.
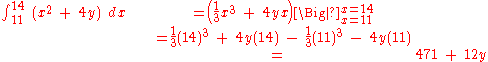
We then integrate the result with respect to y.
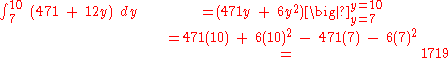
Volumes
The volume of the parallelepipedParallelepipedIn geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, its definition encompasses all four concepts...
of sides 4 × 6 × 5 may be obtained in two ways:- By calculating the double integral of the function f(x, y) = 5 over the region D in the xy-plane which is the base of the parallelepiped.
- By calculating the triple integral of the constant function 1 over the parallelepiped itself
Computing a volume
Using the methods previously described, it is possible to calculate the volumes of some common solids.- CylinderCylinder (geometry)A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...
: The volume of a cylinder with height h and circular base of radius R can be calculated by integrating the constant function h over the circular base, using polar coordinates.
This is in agreement with the formula-
 .
.
- SphereSphereA sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
: The volume of a sphere with radius R can be calculated by integrating the constant function 1 over the sphere, using spherical coordinates.
- TetrahedronTetrahedronIn geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
(triangular pyramidPyramidA pyramid is a structure whose outer surfaces are triangular and converge at a single point. The base of a pyramid can be trilateral, quadrilateral, or any polygon shape, meaning that a pyramid has at least three triangular surfaces...
or 3-simplexSimplexIn geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
): The volume of a tetrahedron with its apex at the origin and edges of length l along the x, y and z axes can be calculated by integrating the constant function 1 over the tetrahedron.
This is in agreement with the formula-
 .
.
Multiple improper integral
In case of unbounded domains or functions not bounded near the boundary of the domain, we have to introduce the double improper integralImproper integralIn calculus, an improper integral is the limit of a definite integral as an endpoint of the interval of integration approaches either a specified real number or ∞ or −∞ or, in some cases, as both endpoints approach limits....
or the triple improper integral.
Multiple integrals and iterated integrals
Fubini's theoremFubini's theoremIn mathematical analysis Fubini's theorem, named after Guido Fubini, is a result which gives conditions under which it is possible to compute a double integral using iterated integrals. As a consequence it allows the order of integration to be changed in iterated integrals.-Theorem...
states that if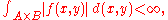
that is, if the integral is absolutely convergent, then the multiple integral will give the same result as the iterated integral,
In particular this will occur if |f(x,y)| is a bounded functionBounded functionIn mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...
and A and B are bounded setBounded setIn mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
s.
If the integral is not absolutely convergent, care is needed not to confuse the concepts of multiple integral and iterated integral, especially since the same notation is often used for either concept. The notation
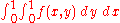
means, in some cases, an iterated integral rather than a true double integral. In an iterated integral, the outer integral

is the integral with respect to x of the following function of x:

A double integral, on the other hand, is defined with respect to area in the xy-plane. If the double integral exists, then it is equal to each of the two iterated integrals (either "dy dx" or "dx dy") and one often computes it by computing either of the iterated integrals. But sometimes the two iterated integrals exist when the double integral does not, and in some such cases the two iterated integrals are different numbers, i.e., one has

This is an instance of rearrangement of a conditionally convergent integral.
The notation
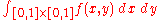
may be used if one wishes to be emphatic about intending a double integral rather than an iterated integral.
Some practical applications
Quite generally, just as in one variable, one can use the multiple integral to find the average of a function over a given set. Given a set D ⊆ Rn and an integrable function f over D, the average value of f over its domain is given by

where m(D) is the measureMeasure (mathematics)In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
of D.
Additionally, multiple integrals are used in many applications in physicsPhysicsPhysics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
. The examples below also show some variations in the notation.
In mechanicsMechanicsMechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
, the moment of inertiaMoment of inertiaIn classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
is calculated as the volume integral (triple integral) of the densityDensityThe mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
weighed with the square of the distance from the axis:
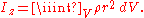
The gravitational potential associated with a mass distributionMass distributionMass distribution is a term used in physics and mechanics and describes the spatial distribution of mass within a solid body. In principle, it is relevant also for gases or liquids, but on earth their mass distribution is almost homogeneous.-Astronomy:...
given by a mass measure dm on three-dimensional Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
R3 is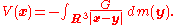
If there is a continuous function ρ(x) representing the density of the distribution at x, so that dm(x) = ρ(x)d 3x, where d 3x is the Euclidean volume elementVolume elementIn mathematics, a volume element provides a means for integrating a function with respect to volume in various coordinate systems such as spherical coordinates and cylindrical coordinates...
, then the gravitational potential is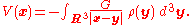
In electromagnetismElectromagnetismElectromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
, Maxwell's equationsMaxwell's equationsMaxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
can be written using multiple integrals to calculate the total magnetic and electric fields. In the following example, the electric fieldElectric fieldIn physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
produced by a distribution of chargesElectric chargeElectric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
given by the volume charge densityCharge densityThe linear, surface, or volume charge density is the amount of electric charge in a line, surface, or volume, respectively. It is measured in coulombs per meter , square meter , or cubic meter , respectively, and represented by the lowercase Greek letter Rho . Since there are positive as well as...
 is obtained by a triple integral of a vector function:
is obtained by a triple integral of a vector function:
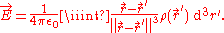
This can also be written as an integral with respect to a signed measureSigned measureIn mathematics, signed measure is a generalization of the concept of measure by allowing it to have negative values. Some authors may call it a charge, by analogy with electric charge, which is a familiar distribution that takes on positive and negative values.-Definition:There are two slightly...
representing the charge distribution.
See also
- Main analysisReal analysisReal analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
theorems that relate multiple integrals:- Divergence theoremDivergence theoremIn vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
- Stokes' theoremStokes' theoremIn differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
- Green's theoremGreen's theoremIn mathematics, Green's theorem gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C...
- Divergence theorem
Free software for multidimensional numerical integration
- interalg: a solver from OpenOptOpenOptOpenOpt is an open-source framework for numerical optimization, nonlinear equations and systems of them. It is licensed under the BSD license, making it available to be used in both open- and closed-code software. The package already has some essential ....
/FuncDesignerFuncDesignerFuncDesigner is a computer algebra system written as a Python module. It is cross-platform software , with a completely free license....
frameworks, based on interval analysis, guaranteed precision, license: BSD (free for any purposes) - Cuba is a free-software library of several multi-dimensional integration algorithms
- Cubature code for adaptive multi-dimensional integration
External links
- Mathematical Assistant on Web online evaluation of double integrals in Cartesian coordinatesCartesian coordinate systemA Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
and polar coordinatesPolar coordinate systemIn mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a fixed point and an angle from a fixed direction....
(includes intermediate steps in the solution, powered by Maxima (software))