Conditional convergence
Encyclopedia
In mathematics
, a series
or integral
is said to be conditionally convergent if it converges, but it does not converge absolutely
.
is said to converge conditionally if
exists and is a finite number (not ∞ or −∞), but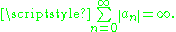 
A classical example is given by
which converges to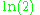
, but is not absolutely convergent (see Harmonic series
).
The simplest examples of conditionally convergent series (including the one above) are the alternating series.
Bernhard Riemann
proved that a conditionally convergent series may be rearranged to converge to any sum at all, including ∞ or −∞; see Riemann series theorem.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
or integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
is said to be conditionally convergent if it converges, but it does not converge absolutely
Absolute convergence
In mathematics, a series of numbers is said to converge absolutely if the sum of the absolute value of the summand or integrand is finite...
.
Definition
More precisely, a series is said to converge conditionally if exists and is a finite number (not ∞ or −∞), but 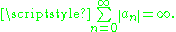A classical example is given by
which converges to
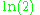, but is not absolutely convergent (see Harmonic seriesHarmonic series (mathematics)
In mathematics, the harmonic series is the divergent infinite series:Its name derives from the concept of overtones, or harmonics in music: the wavelengths of the overtones of a vibrating string are 1/2, 1/3, 1/4, etc., of the string's fundamental wavelength...
).
The simplest examples of conditionally convergent series (including the one above) are the alternating series.
Bernhard Riemann
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
proved that a conditionally convergent series may be rearranged to converge to any sum at all, including ∞ or −∞; see Riemann series theorem.