Kriging
Encyclopedia
Kriging is a group of geostatistical
techniques to interpolate
the value of a random field
(e.g., the elevation, z, of the landscape as a function of the geographic location) at an unobserved location from observations of its value at nearby locations.
The theory behind interpolation and extrapolation by kriging was developed by the French mathematician Georges Matheron
based on the Master's thesis of Daniel Gerhardus Krige, the pioneering plotter of distance-weighted average gold grades at the Witwatersrand
reef complex in South Africa
. The English verb is to krige and the most common noun is kriging; both are often pronounced with a hard "g"
, following the pronunciation of the name "Krige".
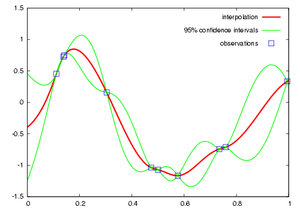Kriging belongs to the family of linear least squares
estimation algorithm
s. As illustrated in Figure 1, the aim of kriging is to estimate the value of an unknown real-valued
function,
, at a point, 
, given the values of the function at some other points, 
. A kriging estimator is said to be linear because the predicted value 
is a linear combination
that may be written as
.
The weights
are solutions of a system of linear equations which is obtained by assuming that 
is a sample-path of a random process
, and that the error of prediction
is to be minimized in some sense. For instance, the so-called simple kriging assumption is that the mean
and the covariance
of
is known and then, the kriging predictor is the one that minimizes the variance
of the prediction error.
To date kriging has been used in a variety of disciplines, including the following:
and many others.
the value
of a random field
(e.g. the elevation 
of the landscape as a function of the geographic location 
) at an unobserved location 
from observations 
of the random field at nearby locations 
. Kriging computes the best linear unbiased estimator 
of 
based on a stochastic
model of the spatial dependence
quantified either by the variogram
or by expectation
and the covariance function
of the random field.
The kriging estimator is given by a linear combination
of the observed values
with weights 
chosen such that the variance (also called kriging variance or kriging error):
is minimized subject to the unbiasedness condition:
The kriging variance must not be confused with the variance
of the kriging predictor
itself.
implied by the unbiasedness condition; i.e. the linear constraint, and hence the method for calculating the weights, depends upon the type of kriging.
Classical methods of kriging are
of the random field
to be known, and relies on a covariance function
. However, in most applications neither the expectation nor the covariance are known beforehand.
and are given by the simple kriging equation system:
This is analogous to a linear regression of
on the other 
.
which leads to the generalised least squares version of the Gauss-Markov theorem (Chiles & Delfiner 1999, p. 159):
The mathematical condition for applicability of ordinary kriging are:
and are given by the ordinary kriging equation system:
the additional parameter
is a Lagrange multiplier used in the minimization of the kriging error 
to honor the unbiasedness condition.
. Both theories derive a best linear unbiased estimator, based on assumptions on covariance
s, make use of Gauss-Markov theorem to prove independence of the estimate and error, and make use of very similar formulae. They are nevertheless useful in different frameworks: kriging is made for interpolation
of a single realisation of a random field, while regression models are based on multiple observations of a multivariate dataset.
In the statistical
community the same technique is also known as Gaussian process
regression, Kolmogorov Wiener prediction, or best linear unbiased prediction.
The kriging interpolation may also be seen as a spline
in a reproducing kernel Hilbert space
, with reproducing kernel given by the covariance function. The difference with the classical kriging approach is provided by the interpretation: while the spline is motivated by a minimum norm interpolation based on a Hilbert space structure, kriging is motivated by an expected squared prediction error based on a stochastic model.
Kriging with polynomial trend surfaces is mathematically identical to generalized least squares
polynomial curve fitting
.
Kriging can also be understood as a form of Bayesian inference
. Kriging starts with a prior distribution
over function
s. This prior takes the form of a Gaussian process:
samples from a function will be normally distributed, where the covariance
between any two samples is the covariance function (or kernel
) of the Gaussian process evaluated at the spatial location of two points. A set of values is then observed, each value associated with a spatial location. Now, a new value can be predicted at any new spatial location, by combining the Gaussian prior with a Gaussian likelihood function
for each of the observed values. The resulting posterior
distribution is also Gaussian, with a mean and covariance that can be simply computed from the observed values, their variance, and the kernel matrix derived from the prior.
based on the Master's thesis of Daniel Gerhardus Krige, the pioneering plotter of distance-weighted average gold grades at the Witwatersrand reef complex. The English verb is to krige and the most common adjective is kriging. The method was called krigeage for the first time in Matheron's 1960 Krigeage d'un Panneau Rectangulaire par sa Périphérie. Matheron, in this Note Géostatistique No 28, derives k*, his estimateur and a precursor to the kriged estimate or kriged estimator. In classical statistics, Matheron's k* is the length-weighted average grade of each of his panneaux in his set. What Matheron failed to derive was var(k*), the variance of his estimateur. On the contrary, he computed the length-weighted average grade of each panneau but did not compute the variance of its central value. In time, he replaced length-weighted average grades for three-dimensional sample spaces such as Matheronian blocks of ore with more abundant distance-weighted average grades for zero-dimensional sample spaces such as Matheronian points.
Geostatistics
Geostatistics is a branch of statistics focusing on spatial or spatiotemporal datasets. Developed originally to predict probability distributions of ore grades for mining operations, it is currently applied in diverse disciplines including petroleum geology, hydrogeology, hydrology, meteorology,...
techniques to interpolate
Interpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
the value of a random field
Random field
A random field is a generalization of a stochastic process such that the underlying parameter need no longer be a simple real or integer valued "time", but can instead take values that are multidimensional vectors, or points on some manifold....
(e.g., the elevation, z, of the landscape as a function of the geographic location) at an unobserved location from observations of its value at nearby locations.
The theory behind interpolation and extrapolation by kriging was developed by the French mathematician Georges Matheron
Georges Matheron
Georges François Paul Marie Matheron was a French mathematician and geologist, known as the founder of geostatistics and a co-founder of mathematical morphology. In 1968 he created the Centre de Géostatistique et de Morphologie Mathématique at the Paris School of Mines in Fontainebleau...
based on the Master's thesis of Daniel Gerhardus Krige, the pioneering plotter of distance-weighted average gold grades at the Witwatersrand
Witwatersrand
The Witwatersrand is a low, sedimentary range of hills, at an elevation of 1700–1800 metres above sea-level, which runs in an east-west direction through Gauteng in South Africa. The word in Afrikaans means "the ridge of white waters". Geologically it is complex, but the principal formations...
reef complex in South Africa
South Africa
The Republic of South Africa is a country in southern Africa. Located at the southern tip of Africa, it is divided into nine provinces, with of coastline on the Atlantic and Indian oceans...
. The English verb is to krige and the most common noun is kriging; both are often pronounced with a hard "g"
Hard and soft g
In the Latin-based orthographies of many European languages , a distinction between hard and soft ⟨g⟩ occurs in which ⟨g⟩ represents two distinct phonemes...
, following the pronunciation of the name "Krige".
Interpolation
Least squares
The method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
estimation algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s. As illustrated in Figure 1, the aim of kriging is to estimate the value of an unknown real-valued
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
function,
, at a point, , given the values of the function at some other points, . A kriging estimator is said to be linear because the predicted value is a linear combinationLinear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
that may be written as
.The weights
are solutions of a system of linear equations which is obtained by assuming that is a sample-path of a random processStochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
, and that the error of predictionis to be minimized in some sense. For instance, the so-called simple kriging assumption is that the mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
and the covariance
Covariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
of
is known and then, the kriging predictor is the one that minimizes the varianceVariance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of the prediction error.
Applications
Although kriging was developed originally for applications in geostatistics, it is a general method of statistical interpolation that can be applied within any discipline to sampled data from random fields that satisfy the appropriate mathematical assumptions.To date kriging has been used in a variety of disciplines, including the following:
- Black box modellingBlack box testingBlack-box testing is a method of software testing that tests the functionality of an application as opposed to its internal structures or workings . Specific knowledge of the application's code/internal structure and programming knowledge in general is not required...
in computer experimentComputer experimentIn the scientific context, a computer experiment refer to mathematical modeling using computer simulation. It has become common to call such experiments in silico...
s - Environmental scienceEnvironmental scienceEnvironmental science is an interdisciplinary academic field that integrates physical and biological sciences, to the study of the environment, and the solution of environmental problems...
- HydrogeologyHydrogeologyHydrogeology is the area of geology that deals with the distribution and movement of groundwater in the soil and rocks of the Earth's crust, . The term geohydrology is often used interchangeably...
- MiningMiningMining is the extraction of valuable minerals or other geological materials from the earth, from an ore body, vein or seam. The term also includes the removal of soil. Materials recovered by mining include base metals, precious metals, iron, uranium, coal, diamonds, limestone, oil shale, rock...
- Natural resourceNatural resourceNatural resources occur naturally within environments that exist relatively undisturbed by mankind, in a natural form. A natural resource is often characterized by amounts of biodiversity and geodiversity existent in various ecosystems....
s - Remote sensingRemote sensingRemote sensing is the acquisition of information about an object or phenomenon, without making physical contact with the object. In modern usage, the term generally refers to the use of aerial sensor technologies to detect and classify objects on Earth by means of propagated signals Remote sensing...
- Real estate appraisalReal estate appraisalReal estate appraisal, property valuation or land valuation is the process of valuing real property. The value usually sought is the property's Market Value. Appraisals are needed because compared to, say, corporate stock, real estate transactions occur very infrequently...
and many others.
General equations
Kriging interpolatesInterpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
the value
of a random fieldRandom field
A random field is a generalization of a stochastic process such that the underlying parameter need no longer be a simple real or integer valued "time", but can instead take values that are multidimensional vectors, or points on some manifold....
(e.g. the elevation of the landscape as a function of the geographic location ) at an unobserved location from observations of the random field at nearby locations . Kriging computes the best linear unbiased estimator of based on a stochasticStochastic
Stochastic refers to systems whose behaviour is intrinsically non-deterministic. A stochastic process is one whose behavior is non-deterministic, in that a system's subsequent state is determined both by the process's predictable actions and by a random element. However, according to M. Kac and E...
model of the spatial dependence
Spatial dependence
In applications of statistics, spatial dependence is the existence of statistical dependence in a collection of random variables or a collection time series of random variables, each of which is associated with a different geographical location...
quantified either by the variogram
Variogram
In spatial statistics the theoretical variogram 2\gamma is a function describing the degree of spatial dependence of a spatial random field or stochastic process Z...
or by expectationExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
and the covariance functionCovariance function
In probability theory and statistics, covariance is a measure of how much two variables change together and the covariance function describes the variance of a random variable process or field...
of the random field.The kriging estimator is given by a linear combination
of the observed values
with weights chosen such that the variance (also called kriging variance or kriging error):is minimized subject to the unbiasedness condition:
The kriging variance must not be confused with the variance
of the kriging predictor
itself.Methods
Depending on the stochastic properties of the random field different types of kriging apply. The type of kriging determines the linear constraint on the weights implied by the unbiasedness condition; i.e. the linear constraint, and hence the method for calculating the weights, depends upon the type of kriging.Classical methods of kriging are
- Simple kriging assumes a known constant trend:
. - Ordinary kriging assumes an unknown constant trend:
. - Universal kriging assumes a general polynomial trend model, such as linear trend model
. - IRFk-kriging assumes
to be an unknown polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
in
. - Indicator kriging uses indicator functions instead of the process itself, in order to estimate transition probabilities.
- Multiple-indicator krigingMultiple-indicator krigingMultiple-indicator kriging is a recent advance on other techniques for mineral deposit modeling and resource block model estimation, such as ordinary kriging....
is a version of indicator kriging working with a family of indicators. However, MIK has fallen out of favour as an interpolation technique in recent years. This is due to some inherent difficulties related to operation and model validation. Conditional simulation is fast becoming the accepted replacement technique in this case. - Disjunctive kriging is a nonlinear generalisation of kriging.
- Lognormal kriging interpolates positive data by means of logarithmLogarithmThe logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
s.
Simple kriging
Simple kriging is mathematically the simplest, but the least general. It assumes the expectationExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of the random field
Random field
A random field is a generalization of a stochastic process such that the underlying parameter need no longer be a simple real or integer valued "time", but can instead take values that are multidimensional vectors, or points on some manifold....
to be known, and relies on a covariance function
Covariance function
In probability theory and statistics, covariance is a measure of how much two variables change together and the covariance function describes the variance of a random variable process or field...
. However, in most applications neither the expectation nor the covariance are known beforehand.
Simple kriging assumptions
The practical assumptions for the application of simple kriging are:- wide sense stationarityStationary processIn the mathematical sciences, a stationary process is a stochastic process whose joint probability distribution does not change when shifted in time or space...
of the field. - The expectation is zero everywhere:
. - Known covariance functionCovariance functionIn probability theory and statistics, covariance is a measure of how much two variables change together and the covariance function describes the variance of a random variable process or field...
Simple kriging equation
The kriging weights of simple kriging have no unbiasedness conditionand are given by the simple kriging equation system:
This is analogous to a linear regression of
on the other .Simple kriging interpolation
The interpolation by simple kriging is given by:Simple kriging error
The kriging error is given by:which leads to the generalised least squares version of the Gauss-Markov theorem (Chiles & Delfiner 1999, p. 159):
Ordinary kriging
Ordinary kriging is the most commonly used type of kriging. It assumes a constant but unknown mean.Typical ordinary kriging assumptions
The typical assumptions for the practical application of ordinary kriging are:- Intrinsic stationarity or wide sense stationarityStationary processIn the mathematical sciences, a stationary process is a stochastic process whose joint probability distribution does not change when shifted in time or space...
of the field - enough observations to estimate the variogramVariogramIn spatial statistics the theoretical variogram 2\gamma is a function describing the degree of spatial dependence of a spatial random field or stochastic process Z...
.
The mathematical condition for applicability of ordinary kriging are:
- The mean
is unknown but constant - The variogramVariogramIn spatial statistics the theoretical variogram 2\gamma is a function describing the degree of spatial dependence of a spatial random field or stochastic process Z...
of 
is known.
Ordinary kriging equation
The kriging weights of ordinary kriging fulfill the unbiasedness conditionand are given by the ordinary kriging equation system:
the additional parameter
is a Lagrange multiplier used in the minimization of the kriging error to honor the unbiasedness condition.Ordinary kriging interpolation
The interpolation by ordinary kriging is given by:Ordinary kriging error
The kriging error is given by:Properties
(Cressie 1993, Chiles&Delfiner 1999, Wackernagel 1995)- The kriging estimation is unbiased:
- The kriging estimation honors the actually observed value:
(assuming no measurement error is incurred) - The kriging estimation
is the best linear unbiased estimator of 
if the assumptions hold. However (e.g. Cressie 1993):
- As with any method: If the assumptions do not hold, kriging might be bad.
- There might be better nonlinear and/or biased methods.
- No properties are guaranteed, when the wrong variogram is used. However typically still a 'good' interpolation is achieved.
- Best is not necessarily good: e.g. In case of no spatial dependence the kriging interpolation is only as good as the arithmetic mean.
- Kriging provides
as a measure of precision. However this measure relies on the correctness of the variogram.
Terms
A series of related terms were also named after Krige, including kriged estimate, kriged estimator, kriging variance, kriging covariance, zero kriging variance, unity kriging covariance, kriging matrix, kriging method, kriging model, kriging plan, kriging process, kriging system, block kriging, co-kriging, disjunctive kriging, linear kriging, ordinary kriging, point kriging, random kriging, regular grid kriging, simple kriging and universal kriging.Related methods
Kriging is mathematically closely related to regression analysisRegression analysis
In statistics, regression analysis includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables...
. Both theories derive a best linear unbiased estimator, based on assumptions on covariance
Covariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
s, make use of Gauss-Markov theorem to prove independence of the estimate and error, and make use of very similar formulae. They are nevertheless useful in different frameworks: kriging is made for interpolation
Interpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
of a single realisation of a random field, while regression models are based on multiple observations of a multivariate dataset.
In the statistical
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
community the same technique is also known as Gaussian process
Gaussian process
In probability theory and statistics, a Gaussian process is a stochastic process whose realisations consist of random values associated with every point in a range of times such that each such random variable has a normal distribution...
regression, Kolmogorov Wiener prediction, or best linear unbiased prediction.
The kriging interpolation may also be seen as a spline
Spline (mathematics)
In mathematics, a spline is a sufficiently smooth piecewise-polynomial function. In interpolating problems, spline interpolation is often preferred to polynomial interpolation because it yields similar results, even when using low-degree polynomials, while avoiding Runge's phenomenon for higher...
in a reproducing kernel Hilbert space
Reproducing kernel Hilbert space
In functional analysis , a reproducing kernel Hilbert space is a Hilbert space of functions in which pointwise evaluation is a continuous linear functional. Equivalently, they are spaces that can be defined by reproducing kernels...
, with reproducing kernel given by the covariance function. The difference with the classical kriging approach is provided by the interpretation: while the spline is motivated by a minimum norm interpolation based on a Hilbert space structure, kriging is motivated by an expected squared prediction error based on a stochastic model.
Kriging with polynomial trend surfaces is mathematically identical to generalized least squares
Generalized least squares
In statistics, generalized least squares is a technique for estimating the unknown parameters in a linear regression model. The GLS is applied when the variances of the observations are unequal , or when there is a certain degree of correlation between the observations...
polynomial curve fitting
Curve fitting
Curve fitting is the process of constructing a curve, or mathematical function, that has the best fit to a series of data points, possibly subject to constraints. Curve fitting can involve either interpolation, where an exact fit to the data is required, or smoothing, in which a "smooth" function...
.
Kriging can also be understood as a form of Bayesian inference
Bayesian inference
In statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
. Kriging starts with a prior distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
over function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s. This prior takes the form of a Gaussian process:
samples from a function will be normally distributed, where the covarianceCovariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
between any two samples is the covariance function (or kernel
Kernel (mathematics)
In mathematics, the word kernel has several meanings. Kernel may mean a subset associated with a mapping:* The kernel of a mapping is the set of elements that map to the zero element , as in kernel of a linear operator and kernel of a matrix...
) of the Gaussian process evaluated at the spatial location of two points. A set of values is then observed, each value associated with a spatial location. Now, a new value can be predicted at any new spatial location, by combining the Gaussian prior with a Gaussian likelihood function
Likelihood function
In statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
for each of the observed values. The resulting posterior
Posterior probability
In Bayesian statistics, the posterior probability of a random event or an uncertain proposition is the conditional probability that is assigned after the relevant evidence is taken into account...
distribution is also Gaussian, with a mean and covariance that can be simply computed from the observed values, their variance, and the kernel matrix derived from the prior.
History
The theory of kriging was developed by the French mathematician Georges MatheronGeorges Matheron
Georges François Paul Marie Matheron was a French mathematician and geologist, known as the founder of geostatistics and a co-founder of mathematical morphology. In 1968 he created the Centre de Géostatistique et de Morphologie Mathématique at the Paris School of Mines in Fontainebleau...
based on the Master's thesis of Daniel Gerhardus Krige, the pioneering plotter of distance-weighted average gold grades at the Witwatersrand reef complex. The English verb is to krige and the most common adjective is kriging. The method was called krigeage for the first time in Matheron's 1960 Krigeage d'un Panneau Rectangulaire par sa Périphérie. Matheron, in this Note Géostatistique No 28, derives k*, his estimateur and a precursor to the kriged estimate or kriged estimator. In classical statistics, Matheron's k* is the length-weighted average grade of each of his panneaux in his set. What Matheron failed to derive was var(k*), the variance of his estimateur. On the contrary, he computed the length-weighted average grade of each panneau but did not compute the variance of its central value. In time, he replaced length-weighted average grades for three-dimensional sample spaces such as Matheronian blocks of ore with more abundant distance-weighted average grades for zero-dimensional sample spaces such as Matheronian points.
See also
- Bayes linear statistics
- Gaussian processGaussian processIn probability theory and statistics, a Gaussian process is a stochastic process whose realisations consist of random values associated with every point in a range of times such that each such random variable has a normal distribution...
- Multiple-indicator krigingMultiple-indicator krigingMultiple-indicator kriging is a recent advance on other techniques for mineral deposit modeling and resource block model estimation, such as ordinary kriging....
- Sampling variogram
- Spatial dependenceSpatial dependenceIn applications of statistics, spatial dependence is the existence of statistical dependence in a collection of random variables or a collection time series of random variables, each of which is associated with a different geographical location...
- VariogramVariogramIn spatial statistics the theoretical variogram 2\gamma is a function describing the degree of spatial dependence of a spatial random field or stochastic process Z...
- Multivariate interpolationMultivariate interpolationIn numerical analysis, multivariate interpolation or spatial interpolation is interpolation on functions of more than one variable.The function to be interpolated is known at given points and the interpolation problem consist of yielding values at arbitrary points .-Regular grid:For function...
Books
- Abramowitz, M., and Stegun, I. (1972), Handbook of Mathematical Functions, Dover Publications, New York.
- Banerjee, S., Carlin, B.P. and Gelfand, A.E. (2004). Hierarchical Modeling and Analysis for Spatial Data. Chapman and Hall/CRC Press, Taylor and Francis Group.
- Chiles, J.-P. and P. Delfiner (1999) Geostatistics, Modeling Spatial uncertainty, Wiley Series in Probability and statistics.
- Cressie, N (1993) Statistics for spatial data, Wiley, New York
- David, M (1988) Handbook of Applied Advanced Geostatistical Ore Reserve Estimation, Elsevier Scientific Publishing
- Deutsch, C.V., and Journel, A. G. (1992), GSLIB - Geostatistical Software Library and User's Guide, Oxford University Press, New York, 338 pp.
- Goovaerts, P. (1997) Geostatistics for Natural Resources Evaluation, Oxford University Press, New York
- Isaaks, E. H., and Srivastava, R. M. (1989), An Introduction to Applied Geostatistics, Oxford University Press, New York, 561 pp.
- Journel, A. G. and C. J. Huijbregts (1978) Mining Geostatistics, Academic Press London
- Journel, A. G. (1989), Fundamentals of Geostatistics in Five Lessons, American Geophysical Union, Washington D.C.. Also, "Section 15.9. Gaussian Process Regression".
- Stein, M. L. (1999), Statistical Interpolation of Spatial Data: Some Theory for Kriging, Springer, New York.
- Wackernagel, H. (1995) Multivariate Geostatistics - An Introduction with Applications, Springer Berlin
Historical references
- Agterberg, F P, Geomathematics, Mathematical Background and Geo-Science Applications, Elsevier Scientific Publishing Company, Amsterdam, 1974
- Cressie, N. A. C., The Origins of Kriging, Mathematical Geology, v. 22, pp 239–252, 1990
- Krige, D.G, A statistical approach to some mine valuations and allied problems at the Witwatersrand, Master's thesis of the University of Witwatersrand, 1951
- Link, R F and Koch, G S, Experimental Designs and Trend-Surface Analsysis, Geostatistics, A colloquium, Plenum Press, New York, 1970
- Matheron, G., "Principles of geostatistics", Economic Geology, 58, pp 1246–1266, 1963
- Matheron, G., "The intrinsic random functions, and their applications", Adv. Appl. Prob., 5, pp 439–468, 1973
- Merriam, D F, Editor, Geostatistics, a colloquium, Plenum Press, New York, 1970