Multivariate interpolation
Encyclopedia
In numerical analysis
, multivariate interpolation or spatial interpolation is interpolation
on functions of more than one variable.
The function to be interpolated is known at given points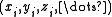
and the interpolation problem consist of yielding values at arbitrary points 
.
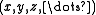(having predetermined, not necessarily uniform, spacing), the following methods are available.
Bitmap resampling is the application of 2D multivariate interpolation in image processing
.
Three of the methods applied on the same dataset, from 16 values located at the black dots. The colours represent the interpolated values.
See also Padua points
, for polynomial interpolation
in two variables.
See also bitmap resampling.
The cubic Hermite spline
article will remind you that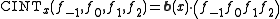
for some 4-vector 
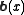which is a function of x alone, where 
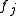is the value at 
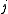of the function to be interpolated.
Rewrite this approximation as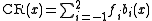
This formula can be directly generalized to N dimensions :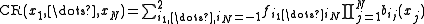
Note that similar generalizations can be made for other types of spline interpolations, including Hermite splines.
In regards to efficiency, the general formula can in fact be computed as a composition of successive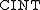
-type operations for any type of tensor product splines, as explained in the tricubic interpolation
article.
However, the fact remains that if there are
terms in the 1-dimensional 
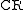-like summation, then there will be 
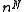terms in the 
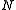-dimensional summation.
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, multivariate interpolation or spatial interpolation is interpolation
Interpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
on functions of more than one variable.
The function to be interpolated is known at given points
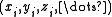and the interpolation problem consist of yielding values at arbitrary points 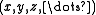.Regular grid
For function values known on a regular gridRegular grid
A regular grid is a tessellation of n-dimensional Euclidean space by congruent parallelotopes . Grids of this type appear on graph paper and may be used in finite element analysis as well as finite volume methods and finite difference methods...
(having predetermined, not necessarily uniform, spacing), the following methods are available.
2 dimensions
- Bilinear interpolationBilinear interpolationIn mathematics, bilinear interpolation is an extension of linear interpolation for interpolating functions of two variables on a regular grid. The interpolated function should not use the term of x^2 or y^2, but x y, which is the bilinear form of x and y.The key idea is to perform linear...
- Bicubic interpolationBicubic interpolationIn mathematics, bicubic interpolation is an extension of cubic interpolation for interpolating data points on a two dimensional regular grid. The interpolated surface is smoother than corresponding surfaces obtained by bilinear interpolation or nearest-neighbor interpolation...
- Bézier surfaceBézier surfaceBézier surfaces are a species of mathematical spline used in computer graphics, computer-aided design, and finite element modeling.As with the Bézier curve, a Bézier surface is defined by a set of control points...
- Lanczos resamplingLanczos resamplingLanczos resampling is an interpolation method used to compute new values for sampled data. It is often used in multivariate interpolation, for example for image scaling , but can be used for any other digital signal...
- Delaunay triangulationDelaunay triangulationIn mathematics and computational geometry, a Delaunay triangulation for a set P of points in a plane is a triangulation DT such that no point in P is inside the circumcircle of any triangle in DT. Delaunay triangulations maximize the minimum angle of all the angles of the triangles in the...
- Spline interpolationSpline interpolationIn the mathematical field of numerical analysis, spline interpolation is a form of interpolation where the interpolant is a special type of piecewise polynomial called a spline. Spline interpolation is preferred over polynomial interpolation because the interpolation error can be made small even...
- Natural neighborNatural neighbor300px|thumb|right|Natural neighbor interpolation. The colored circles. which represent the interpolating weights, wi, are generated using the ratio of the shaded area to that of the cell area of the surrounding points...
- KrigingKrigingKriging is a group of geostatistical techniques to interpolate the value of a random field at an unobserved location from observations of its value at nearby locations....
- Inverse distance weightingInverse distance weightingInverse distance weighting is a method for multivariate interpolation, a process of assigning values to unknown points by using values from usually scattered set of known points...
Bitmap resampling is the application of 2D multivariate interpolation in image processing
Image processing
In electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
.
Three of the methods applied on the same dataset, from 16 values located at the black dots. The colours represent the interpolated values.
See also Padua points
Padua points
In polynomial interpolation of two variables, the Padua points are the first known example of unisolvent point set with minimal growth of their Lebesgue constant, proven to be O.Their name is due to the University of Padua, where they were originally discovered.The points are defined...
, for polynomial interpolation
Polynomial interpolation
In numerical analysis, polynomial interpolation is the interpolation of a given data set by a polynomial: given some points, find a polynomial which goes exactly through these points.- Applications :...
in two variables.
3 dimensions
- Trilinear interpolationTrilinear interpolationTrilinear interpolation is a method of multivariate interpolation on a 3-dimensional regular grid. It approximates the value of an intermediate point within the local axial rectangular prism linearly, using data on the lattice points...
- Tricubic interpolationTricubic interpolationIn the mathematical subfield numerical analysis, tricubic interpolation is a method for obtaining values at arbitrary points in 3D space of a function defined on a regular grid...
See also bitmap resampling.
Tensor product splines for N dimensions
Catmull-Rom splines can be easily generalized to any number of dimensions.The cubic Hermite spline
Cubic Hermite spline
In the mathematical subfield of numerical analysis a cubic Hermite spline , named in honor of Charles Hermite, is a third-degree spline with each polynomial of the spline in Hermite form...
article will remind you that
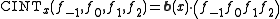for some 4-vector 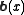which is a function of x alone, where 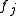is the value at 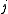of the function to be interpolated.Rewrite this approximation as
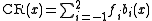
This formula can be directly generalized to N dimensions :
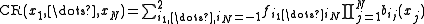
Note that similar generalizations can be made for other types of spline interpolations, including Hermite splines.
In regards to efficiency, the general formula can in fact be computed as a composition of successive
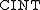-type operations for any type of tensor product splines, as explained in the tricubic interpolationTricubic interpolation
In the mathematical subfield numerical analysis, tricubic interpolation is a method for obtaining values at arbitrary points in 3D space of a function defined on a regular grid...
article.
However, the fact remains that if there are
terms in the 1-dimensional 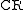-like summation, then there will be 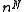terms in the 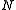-dimensional summation.Irregular grid (scattered data)
Schemes defined for scattered data on a irregular grid should all work on a regular grid, typically reducing to another known method.- Nearest-neighbor interpolation
- Triangulated irregular networkTriangulated irregular networkA triangulated irregular network is a digital data structure used in a geographic information system for the representation of a surface...
-based natural neighborNatural neighbor300px|thumb|right|Natural neighbor interpolation. The colored circles. which represent the interpolating weights, wi, are generated using the ratio of the shaded area to that of the cell area of the surrounding points... - Triangulated irregular networkTriangulated irregular networkA triangulated irregular network is a digital data structure used in a geographic information system for the representation of a surface...
-based linear interpolationLinear interpolationLinear interpolation is a method of curve fitting using linear polynomials. Lerp is an abbreviation for linear interpolation, which can also be used as a verb .-Linear interpolation between two known points:...
(a type of piecewise linear function) - Inverse distance weightingInverse distance weightingInverse distance weighting is a method for multivariate interpolation, a process of assigning values to unknown points by using values from usually scattered set of known points...
- KrigingKrigingKriging is a group of geostatistical techniques to interpolate the value of a random field at an unobserved location from observations of its value at nearby locations....
- Radial basis functionRadial basis functionA radial basis function is a real-valued function whose value depends only on the distance from the origin, so that \phi = \phi; or alternatively on the distance from some other point c, called a center, so that \phi = \phi...
- Thin plate splineThin plate splineThis is a brief derivation for the closed form solutions for smoothing Thin Plate Spline. Details about these splines can be found in ....
- Polyharmonic splinePolyharmonic splineIn mathematics, polyharmonic splines are used forfunction approximation and data interpolation.They are very useful for interpolation of scattered datain many dimensions.- Definition :Polyharmonic splines are a special case of radial basis functions and...
(the thin-plate-spline is a special case of a polyharmonic spline) - Least-squares splineSpline (mathematics)In mathematics, a spline is a sufficiently smooth piecewise-polynomial function. In interpolating problems, spline interpolation is often preferred to polynomial interpolation because it yields similar results, even when using low-degree polynomials, while avoiding Runge's phenomenon for higher...
External links
- Example C++ code for several 1D, 2D and 3D spline interpolations (including Catmull-Rom splines).
- Multi-dimensional Hermite Interpolation and Approximation, Prof. Chandrajit Bajaja, Purdue UniversityPurdue UniversityPurdue University, located in West Lafayette, Indiana, U.S., is the flagship university of the six-campus Purdue University system. Purdue was founded on May 6, 1869, as a land-grant university when the Indiana General Assembly, taking advantage of the Morrill Act, accepted a donation of land and...