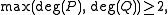Classification of Fatou components
Encyclopedia
In mathematics
, if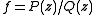 is a rational function
is a rational function
defined in the extended complex plane, and if
then for a periodic component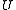 of the Fatou set, exactly one of the following holds:
of the Fatou set, exactly one of the following holds:
One can prove that case 3 only occurs when f(z) is analytically conjugate
to a Euclidean rotation of the unit disc onto itself, and case 4 only occurs when f(z) is analytically conjugate to a Euclidean rotation of some annulus
onto itself.
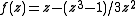 that contains the attracting points that are the solutions to
that contains the attracting points that are the solutions to 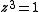 . This is because the map is the one to use for finding solutions to the equation
. This is because the map is the one to use for finding solutions to the equation  by Newton-Raphson formula. The solutions must naturally be attracting fixed points.
by Newton-Raphson formula. The solutions must naturally be attracting fixed points.

and t = 0.6151732... will produce a Herman ring. It is shown by Shishikura that the degree of such map must be at least 3, as in this example.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, if
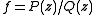 is a rational function
is a rational functionRational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
defined in the extended complex plane, and if
then for a periodic component
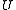 of the Fatou set, exactly one of the following holds:
of the Fatou set, exactly one of the following holds:-
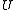 contains an attracting periodic point
contains an attracting periodic point -
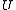 is parabolic
is parabolic -
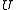 is a Siegel disc
is a Siegel disc -
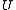 is a Herman ringHerman ringIn the mathematical discipline known as complex dynamics for rational functions, the Herman ring is a Fatou component. where the rational function is conformally conjugate to a irrational rotation of the standard annulus.-Formal definition:...
is a Herman ringHerman ringIn the mathematical discipline known as complex dynamics for rational functions, the Herman ring is a Fatou component. where the rational function is conformally conjugate to a irrational rotation of the standard annulus.-Formal definition:...
.
One can prove that case 3 only occurs when f(z) is analytically conjugate
to a Euclidean rotation of the unit disc onto itself, and case 4 only occurs when f(z) is analytically conjugate to a Euclidean rotation of some annulus
Annulus (mathematics)
In mathematics, an annulus is a ring-shaped geometric figure, or more generally, a term used to name a ring-shaped object. Or, it is the area between two concentric circles...
onto itself.
Attracting periodic point
The components of the map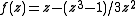 that contains the attracting points that are the solutions to
that contains the attracting points that are the solutions to 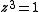 . This is because the map is the one to use for finding solutions to the equation
. This is because the map is the one to use for finding solutions to the equation  by Newton-Raphson formula. The solutions must naturally be attracting fixed points.
by Newton-Raphson formula. The solutions must naturally be attracting fixed points.Herman ring
The map
and t = 0.6151732... will produce a Herman ring. It is shown by Shishikura that the degree of such map must be at least 3, as in this example.