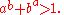Inequality
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an inequality is a statement how the relative size or order of two objects, or about whether they are the same or not (See also: equality).
- The notation a < b means that a is less than b.
- The notation a > b means that a is greater than b.
- The notation a ≠ b means that a is not equal to b, but does not say that one is greater than the other or even that they can be compared in size.
In each statement above, a is not equal to b. These relations are known as strict inequalities. The notation a < b may also be read as "a is strictly less than b".
In contrast to strict inequalities, there are two types of inequality statements that are not strict:
- The notation a ≤ b means that a is less than or equal to b (or, equivalently, not greater than b)
- The notation a ≥ b means that a is greater than or equal to b (or, equivalently, not less than b)
An additional use of the notation is to show that one quantity is much greater than another, normally by several orders of magnitude.
- The notation a b means that a is much less than b. (In measure theory, it denotes instead absolute continuity.)
- The notation a b means that a is much greater than b.
If the sense of the inequality is the same for all values of the variables for which its members are defined, then the inequality is called an "absolute" or "unconditional" inequality. If the sense of an inequality holds only for certain values of the variables involved, but is reversed or destroyed for other values of the variables, it is called a conditional inequality.
Properties
Inequalities are governed by the following propertiesProperty (philosophy)
In modern philosophy, logic, and mathematics a property is an attribute of an object; a red object is said to have the property of redness. The property may be considered a form of object in its own right, able to possess other properties. A property however differs from individual objects in that...
. Note that, for the transitivity, reversal, addition and subtraction, and multiplication and division properties, the property also holds if strict inequality signs (< and >) are replaced with their corresponding non-strict inequality sign (≤ and ≥).
Transitivity
The transitivityTransitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
of inequalities states:
- For any real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, a, b, c:- If a > b and b > c; then a > c
- If a < b and b < c; then a < c
- If a > b and b = c; then a > c
- If a < b and b = c; then a < c'
Addition and subtraction
The properties that deal with additionAddition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
and subtraction
Subtraction
In arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
state:
- For any real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, a, b, c:- If
- If a > b, then a + c > b + c and a − c > b − c
i.e., the real numbers are an ordered group
Ordered group
In abstract algebra, a partially-ordered group is a group equipped with a partial order "≤" that is translation-invariant; in other words, "≤" has the property that, for all a, b, and g in G, if a ≤ b then a+g ≤ b+g and g+a ≤ g+b.An element x of G is called positive element if 0 ≤ x...
Multiplication and division
The properties that deal with multiplicationMultiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
and division
Division (mathematics)
right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
state:
- For any real numbers, a, b, and non-zero c
- If
- If c is negative and a < b, then ac > bc and a/c > b/c
More generally this applies for an ordered field
Ordered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
, see below.
Additive inverse
The properties for the additive inverseAdditive inverse
In mathematics, the additive inverse, or opposite, of a number a is the number that, when added to a, yields zero.The additive inverse of a is denoted −a....
state:
- For any real numbers a and b
- If
- If a > b then −a < −b
Multiplicative inverse
The properties for the multiplicative inverseMultiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
state:
- For any non-zero real numbers a and b that are both positive or both negative
- If
- If a > b then 1/a < 1/b
- If either a or b is negative (but not both) then
- If a < b then 1/a < 1/b
- If a > b then 1/a > 1/b
Applying a function to both sides
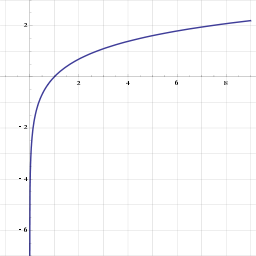
Monotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
ally increasing function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
may be applied to both sides of an inequality and it will still hold. Applying a strictly monotonically decreasing function to both sides of an inequality means the opposite inequality now holds. The rules for additive and multiplicative inverses are both examples of applying a monotonically decreasing function.
For a non-strict inequality (a ≤ b, a ≥ b):
- Applying a monotonically increasing function preserves the relation (≤ remains ≤, ≥ remains ≥)
- Applying a monotonically decreasing function reverses the relation (≤ becomes ≥, ≥ becomes ≤)
As an example, consider the application of the natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
to both sides of an inequality:
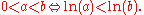
This is true because the natural logarithm is a strictly increasing function.dfjgerpou[ b
Ordered fields
If (F, +, ×) is a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
and ≤ is a total order
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
on F, then (F, +, ×, ≤) is called an ordered field
Ordered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
if and only if:
Note that both (Q, +, ×, ≤) and (R, +, ×, ≤) are ordered field
Ordered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
s, but ≤ cannot be defined in order to make (C, +, ×, ≤) an ordered field
Ordered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
, because −1 is the square of i and would therefore be positive.
The non-strict inequalities ≤ and ≥ on real numbers are total order
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
s. The strict inequalities < and > on real numbers are strict total orders.
Chained notation
The notation a < b < c stands for "a < b and b < c", from which, by the transitivity property above, it also follows that a < c. Obviously, by the above laws, one can add/subtract the same number to all three terms, or multiply/divide all three terms by same nonzero number and reverse all inequalities according to sign. Hence, for example, a < b + e < c is equivalent to a − e < b < c − e.This notation can be generalized to any number of terms: for instance, a1 ≤ a2 ≤ ... ≤ an means that ai ≤ ai+1 for i = 1, 2, ..., n − 1. By transitivity, this condition is equivalent to ai ≤ aj for any 1 ≤ i ≤ j ≤ n.
When solving inequalities using chained notation, it is possible and sometimes necessary to evaluate the terms independently. For instance to solve the inequality 4x < 2x + 1 ≤ 3x + 2, it is not possible to isolate x in any one part of the inequality through addition or subtraction. Instead, the inequalities must be solved independently, yielding x < 1/2 and x ≥ −1 respectively, which can be combined into the final solution −1 ≤ x < 1/2.
Occasionally, chained notation is used with inequalities in different directions, in which case the meaning is the logical conjunction
Logical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
of the inequalities between adjacent terms. For instance, a < b = c ≤ d means that a < b, b = c, and c ≤ d. This notation exists in a few programming language
Programming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
s such as Python
Python (programming language)
Python is a general-purpose, high-level programming language whose design philosophy emphasizes code readability. Python claims to "[combine] remarkable power with very clear syntax", and its standard library is large and comprehensive...
.
Inequalities between means
There are many inequalities between means. For example, for any positive numbers a1, a2, …, an we have where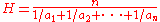 |
(harmonic mean Harmonic mean In mathematics, the harmonic mean is one of several kinds of average. Typically, it is appropriate for situations when the average of rates is desired.... ), |
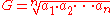 |
(geometric mean Geometric mean The geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the... ), |
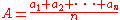 |
(arithmetic mean Arithmetic mean In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space... ), |
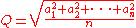 |
(quadratic mean Root mean square In mathematics, the root mean square , also known as the quadratic mean, is a statistical measure of the magnitude of a varying quantity. It is especially useful when variates are positive and negative, e.g., sinusoids... ). |
Power inequalities
Sometimes with notation "power inequality" understand inequalities that contain ab type expressions where a and b are real positive numbers or expressions of some variables. They can appear in exercises of mathematical olympiads and some calculations.Examples
- If x > 0, then
-
-
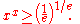
- If x > 0, then
-

- If x, y, z > 0, then
-
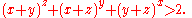
- For any real distinct numbers a and b,
-
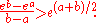
- If x, y > 0 and 0 < p < 1, then
-

- If x, y, z > 0, then
-
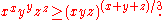
- If a, b > 0, then
-

-
- This inequality was solved by I.Ilani in JSTOR,AMM,Vol.97,No.1,1990.
- If a, b > 0, then
- This inequality was solved by S.Manyama in AJMAA,Vol.7,Issue 2,No.1,2010 and by V.Cirtoaje in JNSA,Vol.4,Issue 2,130-137,2011.
- If a, b > 0, then
- This result was generalized by R. Ozols in 2002 who proved that if a1, ..., an > 0, then
-
- (result is published in Latvian popular-scientific quarterly The Starry Sky, see references).
Well-known inequalities
See also list of inequalities.Mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
s often use inequalities to bound quantities for which exact formulas cannot be computed easily. Some inequalities are used so often that they have names:
Complex numbers and inequalities
The set of complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s
 with its operations of addition
with its operations of additionAddition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
and multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
is a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, but it is impossible to define any relation ≤ so that
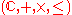 becomes an ordered field
becomes an ordered fieldOrdered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
. To make
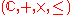 an ordered field
an ordered fieldOrdered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
, it would have to satisfy the following two properties:
- if a ≤ b then a + c ≤ b + c
- if 0 ≤ a and 0 ≤ b then 0 ≤ a b
Because ≤ is a total order
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
, for any number a, either 0 ≤ a or a ≤ 0 (in which case the first property above implies that 0 ≤
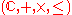 ). In either case 0 ≤ a2; this means that
). In either case 0 ≤ a2; this means that  and
and  ; so
; so  and
and  , which means
, which means  ; contradiction.
; contradiction.However, an operation ≤ can be defined so as to satisfy only the first property (namely, "if a ≤ b then a + c ≤ b + c"). Sometimes the lexicographical order
Lexicographical order
In mathematics, the lexicographic or lexicographical order, , is a generalization of the way the alphabetical order of words is based on the alphabetical order of letters.-Definition:Given two partially ordered sets A and B, the lexicographical order on...
definition is used:
- a ≤ b if
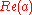 <
< 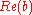 or (
or (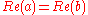 and
and 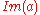 ≤
≤ 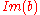 )
)
It can easily be proven that for this definition a ≤ b implies a + c ≤ b + c.
Vector inequalities
Inequality relationships similar to those defined above can also be defined for column vector. If we let the vectors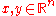 (meaning that
(meaning that 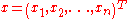 and
and 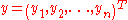 where
where 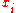 and
and 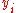 are real numbers for
are real numbers for  ), we can define the following relationships.
), we can define the following relationships.-
 if
if 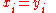 for
for 
-
 if
if 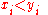 for
for 
-
 if
if 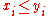 for
for  and
and 
-
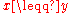 if
if 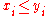 for
for 
Similarly, we can define relationships for
 ,
,  , and
, and  . We note that this notation is consistent with that used by Matthias Ehrgott in Multicriteria Optimization (see References).
. We note that this notation is consistent with that used by Matthias Ehrgott in Multicriteria Optimization (see References).We observe that the property of Trichotomy (as stated above) is not valid for vector relationships. We consider the case where
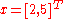 and
and 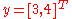 . There exists no valid inequality relationship between these two vectors. Also, a multiplicative inverse
. There exists no valid inequality relationship between these two vectors. Also, a multiplicative inverseMultiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
would need to be defined on a vector before this property could be considered. However, for the rest of the aforementioned properties, a parallel property for vector inequalities exists.
See also
- Binary relationBinary relationIn mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
- BracketBracketBrackets are tall punctuation marks used in matched pairs within text, to set apart or interject other text. In the United States, "bracket" usually refers specifically to the "square" or "box" type.-List of types:...
for the use of the < and > signs as brackets - Fourier-Motzkin elimination
- Inclusion (set theory)
- InequationInequationIn mathematics, an inequation is a statement that two objects or expressions are not the same, or do not represent the same value. This relation is written with a crossed-out equal sign as inx \neq y....
- Interval (mathematics)Interval (mathematics)In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
- List of inequalities
- Partially ordered setPartially ordered setIn mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
- Relational operatorRelational operatorIn computer science, a relational operator is a programming language construct or operator that tests or defines some kind of relation between two entities. These include numerical equality and inequalities...
s, used in programming languages to denote inequality
External links
- Graph of Inequalities by Ed Pegg, Jr.Ed Pegg, Jr.Ed Pegg, Jr. is an expert on mathematical puzzles and is a self-described recreational mathematician. He creates puzzles for the Mathematical Association of America online at Ed Pegg, Jr.'s Math Games. His puzzles have also been used by Will Shortz on the puzzle segment of NPR's Weekend Edition...
, Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
.