
Inequation
Encyclopedia
In mathematics
, an inequation is a statement that two objects or expression
s are not the same, or do not represent the same value. This relation
is written with a crossed-out equal sign ("≠") as in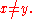
Verbally it may be spoken as "does not equal," or "is unequal to." In programming language
s and electronic communications, the notations
and others, are used instead.
Some sources
use the term inequation synonymously with inequality. Others include ≠ as a type of inequality. In a linearly ordered set
, any inequation implies an inequality: if x ≠ y then x < y or x > y by the trichotomy law.
are:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an inequation is a statement that two objects or expression
Expression (mathematics)
In mathematics, an expression is a finite combination of symbols that is well-formed according to rules that depend on the context. Symbols can designate numbers , variables, operations, functions, and other mathematical symbols, as well as punctuation, symbols of grouping, and other syntactic...
s are not the same, or do not represent the same value. This relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
is written with a crossed-out equal sign ("≠") as in
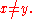
Verbally it may be spoken as "does not equal," or "is unequal to." In programming language
Programming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
s and electronic communications, the notations
x != yx /= yx <> y
and others, are used instead.
Some sources
use the term inequation synonymously with inequality. Others include ≠ as a type of inequality. In a linearly ordered set
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
, any inequation implies an inequality: if x ≠ y then x < y or x > y by the trichotomy law.
Properties
Some useful properties of inequations in algebraElementary algebra
Elementary algebra is a fundamental and relatively basic form of algebra taught to students who are presumed to have little or no formal knowledge of mathematics beyond arithmetic. It is typically taught in secondary school under the term algebra. The major difference between algebra and...
are:
- Any quantity can be addedAdditionAddition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
or subtractedSubtractionIn arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
to both sides. - Both sides can be multipliedMultiplicationMultiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
or dividedDivision (mathematics)right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
by any nonzero quantity. When multiplying or dividing both sides by a negative number, a "<" sign must be changed to a ">" sign and vice-versa in order to retain the truth value. For example 4 < 5 (true), (-1)(4)>(-1)(5), -4 > -5 (still true). - Generally, any injective functionInjective functionIn mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
can be applied to both sides. (This is something of a tautologyTautology (logic)In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
, since injective functions may be defined as functions that always preserve inequations.)
See also
- EquationEquationAn equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
- Equals signEquals signThe equality sign, equals sign, or "=" is a mathematical symbol used to indicate equality. It was invented in 1557 by Robert Recorde. The equals sign is placed between the things stated to have the same value, as in an equation...
- Inequality (mathematics)
- Relational operatorRelational operatorIn computer science, a relational operator is a programming language construct or operator that tests or defines some kind of relation between two entities. These include numerical equality and inequalities...

