
Complex cobordism
Encyclopedia
In mathematics, complex cobordism is a generalized cohomology theory related to cobordism
of manifold
s. Its spectrum
is denoted by MU. It is an exceptionally powerful cohomology
theory, but can be quite hard to compute, so often instead of using it directly one uses some slightly weaker theories derived from it, such as Brown–Peterson cohomology
or Morava K-theory
, that are easier to compute.
The generalized homology and cohomology complex cobordism theories were introduced by using the Thom spectrum.
. Complex bordism is a generalized homology theory
, corresponding to a spectrum MU that can be described explicitly in terms of Thom space
s as follows.
The space MU(n) is the Thom space
of the universal n-plane bundle over the classifying space
BU(n) of the unitary group
U(n). The natural inclusion from U(n) into U(n+1) induces a map from the double suspension S2MU(n) to MU(n+1). Together these maps give the spectrum MU.
Write CP∞ for infinite dimensional complex projective space
, which is the classifying space for complex line bundles, so that tensor product of line bundles induces a map μ:CP∞× CP∞ → CP∞.
A complex orientation on an associative commutative ring spectrum E is an element x in E2(CP∞) whose restriction to E2(CP1)
is 1, if the latter ring is identified with the coefficient ring of E. A spectrum E with such an element x is called a complex oriented ring spectrum.
If E is a complex oriented ring spectrum, then
and μ*(x) ∈ E*(point)
Complex cobordism has a natural complex orientation.
showed that there is a natural isomorphism from its coefficient ring to
Lazard's universal ring
, making the formal group law of complex cobordism into the universal formal group law. In other words, for any formal group law F over any commutative ring R, there is a unique ring homomorphism from MU*(point) to R such that F is the pullback of the formal group law of complex cobordism.
interest is in the torsion of complex cobordism. It is often easier to study the torsion one prime at a time by localizing MU at a prime p; roughly speaking this means one kills off torsion prime to p.
The localization MUp of MU at a prime p splits as a sum of suspensions of a simpler cohomology theory called Brown–Peterson cohomology, first described by . In practice one often does calculations with Brown–Peterson cohomology rather than with complex cobordism. Knowledge of the Brown–Peterson cohomologies of a space for all primes p is roughly equivalent to knowledge of its complex cobordism.
Similarly MU*(BU) is isomorphic to the polynomial ring MU*(point)[β1, β2, ...]
The coproduct is given by
where the notation 2i means take the piece of degree 2i.
This can be interpreted as follows. The map
is a continuous automorphism of the ring of formal power series in x, and the coproduct of MU*(MU) gives the composition of two such automorphisms.
Cobordism
In mathematics, cobordism is a fundamental equivalence relation on the class of compact manifolds of the same dimension, set up using the concept of the boundary of a manifold. Two manifolds are cobordant if their disjoint union is the boundary of a manifold one dimension higher. The name comes...
of manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s. Its spectrum
Spectrum (homotopy theory)
In algebraic topology, a branch of mathematics, a spectrum is an object representing a generalized cohomology theory. There are several different constructions of categories of spectra, any of which gives a context for the same stable homotopy theory....
is denoted by MU. It is an exceptionally powerful cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
theory, but can be quite hard to compute, so often instead of using it directly one uses some slightly weaker theories derived from it, such as Brown–Peterson cohomology
Brown–Peterson cohomology
In mathematics, Brown–Peterson cohomology is a generalized cohomology theory introduced by, depending on a choice of prime p. It is described in detail by .Its representing spectrum is denoted by BP.-Complex cobordism and Quillen's idempotent:...
or Morava K-theory
Morava K-theory
In stable homotopy theory, a branch of mathematics, Morava K-theory is one of a collection of cohomology theories introduced in algebraic topology by Jack Morava in unpublished preprints in the early 1970s...
, that are easier to compute.
The generalized homology and cohomology complex cobordism theories were introduced by using the Thom spectrum.
Spectrum of complex cobordism
The complex bordism MU*(X) of a space X is roughly the group of bordism classes of manifolds over X with a complex linear structure on the stable normal bundleNormal bundle
In differential geometry, a field of mathematics, a normal bundle is a particular kind of vector bundle, complementary to the tangent bundle, and coming from an embedding .-Riemannian manifold:...
. Complex bordism is a generalized homology theory
Homology theory
In mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
, corresponding to a spectrum MU that can be described explicitly in terms of Thom space
Thom space
In mathematics, the Thom space, Thom complex, or Pontryagin-Thom construction of algebraic topology and differential topology is a topological space associated to a vector bundle, over any paracompact space....
s as follows.
The space MU(n) is the Thom space
Thom space
In mathematics, the Thom space, Thom complex, or Pontryagin-Thom construction of algebraic topology and differential topology is a topological space associated to a vector bundle, over any paracompact space....
of the universal n-plane bundle over the classifying space
Classifying space
In mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
BU(n) of the unitary group
Unitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
U(n). The natural inclusion from U(n) into U(n+1) induces a map from the double suspension S2MU(n) to MU(n+1). Together these maps give the spectrum MU.
Formal group laws
and showed that the coefficient ring π*(MU) (equal to the complex cobordism of a point, or equivalently the ring of cobordism classes of stably complex manifolds) is a polynomial ring Z[x1, x2,...] on infinitely many generators xi ∈ π2i(MU) of positive even degrees.Write CP∞ for infinite dimensional complex projective space
Complex projective space
In mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the complex lines...
, which is the classifying space for complex line bundles, so that tensor product of line bundles induces a map μ:CP∞× CP∞ → CP∞.
A complex orientation on an associative commutative ring spectrum E is an element x in E2(CP∞) whose restriction to E2(CP1)
is 1, if the latter ring is identified with the coefficient ring of E. A spectrum E with such an element x is called a complex oriented ring spectrum.
If E is a complex oriented ring spectrum, then
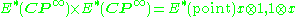
and μ*(x) ∈ E*(point)
Complex cobordism has a natural complex orientation.
showed that there is a natural isomorphism from its coefficient ring to
Lazard's universal ring
Lazard's universal ring
In mathematics, Lazard's universal ring is a ring introduced by over which the universal commutative one-dimensional formal group law is defined....
, making the formal group law of complex cobordism into the universal formal group law. In other words, for any formal group law F over any commutative ring R, there is a unique ring homomorphism from MU*(point) to R such that F is the pullback of the formal group law of complex cobordism.
Brown–Peterson cohomology
Complex cobordism over the rationals can be reduced to ordinary cohomology over the rationals, so the maininterest is in the torsion of complex cobordism. It is often easier to study the torsion one prime at a time by localizing MU at a prime p; roughly speaking this means one kills off torsion prime to p.
The localization MUp of MU at a prime p splits as a sum of suspensions of a simpler cohomology theory called Brown–Peterson cohomology, first described by . In practice one often does calculations with Brown–Peterson cohomology rather than with complex cobordism. Knowledge of the Brown–Peterson cohomologies of a space for all primes p is roughly equivalent to knowledge of its complex cobordism.
Conner–Floyd classes
The ring MU*(BU) is isomorphic to the formal power series ring MU*(point)cf1, cf2, ... where the elements cf are called Conner–Floyd classes. They are the analogues of Chern classes for complex cobordism. They were introduced bySimilarly MU*(BU) is isomorphic to the polynomial ring MU*(point)[β1, β2, ...]
Cohomology operations
The Hopf algebra MU*(MU) is isomorphic to the polynomial algebra R[b1, b2, ...], where R is the reduced bordism ring of a 0-sphere.The coproduct is given by
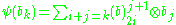
where the notation 2i means take the piece of degree 2i.
This can be interpreted as follows. The map

is a continuous automorphism of the ring of formal power series in x, and the coproduct of MU*(MU) gives the composition of two such automorphisms.
See also
- Adams–Novikov spectral sequence
- List of cohomology theories
- Algebraic cobordismAlgebraic cobordismIn mathematics, algebraic cobordism is an analogue of complex cobordism for smooth quasi-projective schemes over a field. It was introduced by ....
External links
- Complex bordism at the manifold atlas
- cobordism cohomology theory in ncatlab

