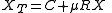Helmert transformation
Encyclopedia
The Helmert transformation (named after Friedrich Robert Helmert
, 1843–1917; also called a seven-parameter transformation) is a transformation method within a three-dimensional space. It is frequently used in geodesy
to produce distortion-free transformations from one datum to another using:
where
The parameter
s are:
Thus, the Helmert transformation is a similarity mapping. It is a special implementation of Galilean transformation
, along with affine transformation
s and projection transformation
s. However, the latter two distort the lengths of line segments.
In practice, it is best to use more points. Through this correspondence, more accuracy is obtained, and a statistical assessment of the results becomes possible. In this case, the calculation is adjusted with the Gaussian least squares
method.
A numerical value for the accuracy of the transformation parameters is obtained by calculating the values at the reference points, and weighting the results relative to the centroid
of the points.
While the method is mathematically rigorous, it is entirely dependent on the rigour of the parameters that are used. In practice, these parameters are computed from the inclusion of at least three known points in the networks. However the accuracy of these will affect the following transformation parameters, as these points will contain observation errors. Therefore a "real-world" transformation will only be a best estimate and should contain a statistical measure of its quality.
It is not always necessary to use the seven parameter transformation, sometimes it is sufficient to use the five parameter transformation, composed of three translations, one longitude rotation and one change of scale.
to transform the coordinates of the point from one coordinate system into another. Using it, it becomes possible to convert regional surveying
points into the WGS84 locations used by GPS
.
In the process, the Gauss–Krüger coordinate, x and y, plus the height, h, are converted into 3D values in steps:
The third step consists of the application of a rotation matrix, multiplication with the
scale factor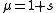
(with a value near 1) and the addition of the three translations, 
, 
, 
.
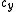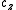The coordinates of a reference system B are derived from reference system A by the following formula:
or for each single parameter of the coordinate:
Friedrich Robert Helmert
Friedrich Robert Helmert was a German geodesist and an important writer on the theory of errors.Helmert was born in Freiberg, Kingdom of Saxony. After schooling in Freiberg and Dresden, he entered the Polytechnische Schule, now Technische Universität, in Dresden to study engineering science in 1859...
, 1843–1917; also called a seven-parameter transformation) is a transformation method within a three-dimensional space. It is frequently used in geodesy
Geodesy
Geodesy , also named geodetics, a branch of earth sciences, is the scientific discipline that deals with the measurement and representation of the Earth, including its gravitational field, in a three-dimensional time-varying space. Geodesists also study geodynamical phenomena such as crustal...
to produce distortion-free transformations from one datum to another using:
where
- XT is the transformed vector
- X is the initial vector
The parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
s are:
— translation vector. Contains the three translationsTranslation (geometry)In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
along the coordinate axes
— scale factorScale factorA scale factor is a number which scales, or multiplies, some quantity. In the equation y=Cx, C is the scale factor for x. C is also the coefficient of x, and may be called the constant of proportionality of y to x...
, which is unitless, and as it is usually expressed in ppm, it must be divided by 1,000,000.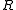
— rotation matrix. Consists of three axes (small rotationRotationA rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
s around the coordinate axes)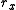
, 
, 
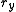. The rotation matrix is an orthogonal matrixOrthogonal matrixIn linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
. The rotation is given in radians.
Thus, the Helmert transformation is a similarity mapping. It is a special implementation of Galilean transformation
Galilean transformation
The Galilean transformation is used to transform between the coordinates of two reference frames which differ only by constant relative motion within the constructs of Newtonian physics. This is the passive transformation point of view...
, along with affine transformation
Affine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
s and projection transformation
Projection (mathematics)
Generally speaking, in mathematics, a projection is a mapping of a set which is idempotent, which means that a projection is equal to its composition with itself. A projection may also refer to a mapping which has a left inverse. Bot notions are strongly related, as follows...
s. However, the latter two distort the lengths of line segments.
Calculating the parameters
If the transformation parameters are unknown, they can be calculated with reference points (that is, points whose coordinates are known before and after the transformation. Since a total of seven parameters (three translations, one scale, three rotations) have to be determined, at least two points and one coordinate of a third point (for example, the Z-coordinate) must be known. This gives a system of linear equations with seven equations and seven unknowns, which can be solved.In practice, it is best to use more points. Through this correspondence, more accuracy is obtained, and a statistical assessment of the results becomes possible. In this case, the calculation is adjusted with the Gaussian least squares
Least squares
The method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
method.
A numerical value for the accuracy of the transformation parameters is obtained by calculating the values at the reference points, and weighting the results relative to the centroid
Centroid
In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...
of the points.
While the method is mathematically rigorous, it is entirely dependent on the rigour of the parameters that are used. In practice, these parameters are computed from the inclusion of at least three known points in the networks. However the accuracy of these will affect the following transformation parameters, as these points will contain observation errors. Therefore a "real-world" transformation will only be a best estimate and should contain a statistical measure of its quality.
It is not always necessary to use the seven parameter transformation, sometimes it is sufficient to use the five parameter transformation, composed of three translations, one longitude rotation and one change of scale.
Two-dimensional case
A special case is the two-dimensional Helmert transformation. Here, only four parameters are needed (two translations, one scaling, one rotation). These can be determined from two known points; if more points are available then checks can be made.Application
The Helmert transformation is used, among other things, in geodesyGeodesy
Geodesy , also named geodetics, a branch of earth sciences, is the scientific discipline that deals with the measurement and representation of the Earth, including its gravitational field, in a three-dimensional time-varying space. Geodesists also study geodynamical phenomena such as crustal...
to transform the coordinates of the point from one coordinate system into another. Using it, it becomes possible to convert regional surveying
Surveying
See Also: Public Land Survey SystemSurveying or land surveying is the technique, profession, and science of accurately determining the terrestrial or three-dimensional position of points and the distances and angles between them...
points into the WGS84 locations used by GPS
Global Positioning System
The Global Positioning System is a space-based global navigation satellite system that provides location and time information in all weather, anywhere on or near the Earth, where there is an unobstructed line of sight to four or more GPS satellites...
.
In the process, the Gauss–Krüger coordinate, x and y, plus the height, h, are converted into 3D values in steps:
- Calculation of the ellipsoidal width, length and height (W, L, H)
- Calculation of X, Y and Z relative to the reference ellipsoidReference ellipsoidIn geodesy, a reference ellipsoid is a mathematically-defined surface that approximates the geoid, the truer figure of the Earth, or other planetary body....
of surveying - 7-parameter transformation (where X, Y and Z change almost evenly, a few hundred metres at most, and the distances change a few mm per km).
- Because of this, terrestrially measured positions can be compared with GPS data; these can then be brought into the surveying as new points — transformed in the opposite order.
The third step consists of the application of a rotation matrix, multiplication with the
scale factor
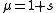(with a value near 1) and the addition of the three translations, , , 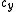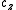.The coordinates of a reference system B are derived from reference system A by the following formula:
or for each single parameter of the coordinate:
-
For the reverse transformation, each element is multiplied by -1.
The seven parameters are determined for each region with three or more "identical points" of both systems. To bring them into agreement, the small inconsistencies (usually only a few cm) are adjusted using the method of least squaresLeast squaresThe method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
– that is, eliminated in a statistically plausible manner.
Standard parameters
Note that the rotation angles given in the table are in seconds and must be converted to radians before use in the calculation.
Region Start datum Target datum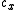 
(MetreMetreThe metre , symbol m, is the base unit of length in the International System of Units . Originally intended to be one ten-millionth of the distance from the Earth's equator to the North Pole , its definition has been periodically refined to reflect growing knowledge of metrology...
)
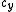(Metre)
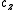(Metre)s (ppm) rx (Arcsecond) ry (Arcsecond) rz (Arcsecond) Slovenia ETRS89 D48 D96 409.545 72.164 486.872 17.919665 −3.085957 −5.469110 11.020289 England EnglandEngland is a country that is part of the United Kingdom. It shares land borders with Scotland to the north and Wales to the west; the Irish Sea is to the north west, the Celtic Sea to the south west, with the North Sea to the east and the English Channel to the south separating it from continental...
, ScotlandScotlandScotland is a country that is part of the United Kingdom. Occupying the northern third of the island of Great Britain, it shares a border with England to the south and is bounded by the North Sea to the east, the Atlantic Ocean to the north and west, and the North Channel and Irish Sea to the...
, WalesWalesWales is a country that is part of the United Kingdom and the island of Great Britain, bordered by England to its east and the Atlantic Ocean and Irish Sea to its west. It has a population of three million, and a total area of 20,779 km²...WGS84 OSGB36 −446.448 125.157 −542.06 20.4894 −0.1502 −0.247 −0.8421 Ireland IrelandIreland is an island to the northwest of continental Europe. It is the third-largest island in Europe and the twentieth-largest island on Earth...WGS84 Ireland 1965 −482.53 130.596 −564.557 −8.15 1.042 0.214 0.631 Germany GermanyGermany , officially the Federal Republic of Germany , is a federal parliamentary republic in Europe. The country consists of 16 states while the capital and largest city is Berlin. Germany covers an area of 357,021 km2 and has a largely temperate seasonal climate...WGS84 DHDN −591.28 −81.35 −396.39 −9.82 1.4770 −0.0736 −1.4580 Germany GermanyGermany , officially the Federal Republic of Germany , is a federal parliamentary republic in Europe. The country consists of 16 states while the capital and largest city is Berlin. Germany covers an area of 357,021 km2 and has a largely temperate seasonal climate...WGS84 Bessel 1841 Bessel ellipsoidThe Bessel ellipsoid is an important reference ellipsoid of geodesy. It is currently used by several countries for their national geodetic surveys, in Europe and on other continents, but will be replaced in the next decades by modern ellipsoids of satellite geodesy.The Bessel ellipsoid was derived...−582 −105 −414 −8.3 −1.04 −0.35 3.08 Germany GermanyGermany , officially the Federal Republic of Germany , is a federal parliamentary republic in Europe. The country consists of 16 states while the capital and largest city is Berlin. Germany covers an area of 357,021 km2 and has a largely temperate seasonal climate...WGS84 Krassovski 1940 −24 123 94 −1.1 −0.02 0.26 0.13 Austria AustriaAustria , officially the Republic of Austria , is a landlocked country of roughly 8.4 million people in Central Europe. It is bordered by the Czech Republic and Germany to the north, Slovakia and Hungary to the east, Slovenia and Italy to the south, and Switzerland and Liechtenstein to the...
(BEV)WGS84 MGI −577.326 −90.129 −463.920 −2.423 5.137 1.474 5.297 USA WGS84 Clarke 1866 8 −160 −176 0 0 0 0
These are standard parameter sets for the 7-parameter transformation (or data transformation) between two ellipsoids. For a transformation in the opposite direction, the signs of all the parameters must be changed. The translations cx, cy, cz are sometimes described as tx, ty, tz, or dx, dy, dz. The rotations x, y, and z are sometimes also described as
, 
and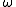 
. In the United Kingdom the prime interest is the transformation between the OSGB36 datum used by the Ordnance survey for Grid References on its Landranger and Explorer maps to the WGS84 implementation used by GPS technology. The Gauss–Krüger coordinate system used in Germany normally refers to the BesselFriedrich Bessel-References:* John Frederick William Herschel, A brief notice of the life, researches, and discoveries of Friedrich Wilhelm Bessel, London: Barclay, 1847 -External links:...
ellipsoid. A further datum of interest was the ED50ED50ED 50 is a geodetic datum which was defined after World War II for the international connection of geodetic networks....
datum based on the Hayford ellipsoidHayford ellipsoidThe Hayford ellipsoid is a geodetic reference ellipsoid, named after the US geodesist John Fillmore Hayford , which was introduced in 1910. The Hayford ellipsoid was also referred to as the International ellipsoid 1924 after it had been adopted by the International Union of Geodesy and Geophysics...
. It is used by NATO for military maps and in future for most EU countries.
The earth does not have a perfect ellipsoidal shape, but is described as a geoidGeoidThe geoid is that equipotential surface which would coincide exactly with the mean ocean surface of the Earth, if the oceans were in equilibrium, at rest , and extended through the continents . According to C.F...
. Instead, the geoid of the earth is described by many ellipsoids. Depending upon the actual location, the "locally best aligned ellipsoid" has been used for surveying and mapping purposes. The standard parameter set gives an accuracy of about 7 m for a OSGB36/WGS84 transformation. This is not precise enough for surveying, and the Ordnance Survey supplements these results by using a lookup table of further translations in order to reach 1 cm accuracy.
Restrictions
The Helmert transformation only uses one scale factor, so it is not suitable for:- The manipulation of measured drawings and photographsPhotographyPhotography is the art, science and practice of creating durable images by recording light or other electromagnetic radiation, either electronically by means of an image sensor or chemically by means of a light-sensitive material such as photographic film...
- The comparison of paper deformations while scanningImage scannerIn computing, an image scanner—often abbreviated to just scanner—is a device that optically scans images, printed text, handwriting, or an object, and converts it to a digital image. Common examples found in offices are variations of the desktop scanner where the document is placed on a glass...
old plans and maps.
In these cases, use another affine transformationAffine transformationIn geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
.
External links
- http://www.w-volk.de/museum/mathex02.htm
- http://www.webcitation.org/query?url=http://www.geocities.com/mapref/savpub/savpub-23.htm%23item40&date=2009-10-26+02:12:14 (Geometry for data exchange)
- http://www.mapref.org/
- The manipulation of measured drawings and photographs