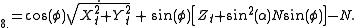Reference ellipsoid
Encyclopedia
In geodesy
, a reference ellipsoid is a mathematically-defined surface that approximates the geoid
, the truer figure of the Earth
, or other planetary body.
Because of their relative simplicity, reference ellipsoids are used as a preferred surface on which geodetic network
computations are performed and point coordinates such as latitude
, longitude
, and elevation
are defined.
with two different axes: An equator
ial radius (the semi-major axis
 ), and a polar radius (the semi-minor axis
), and a polar radius (the semi-minor axis
 ). More rarely, a scalene ellipsoid with three axes (triaxial——
). More rarely, a scalene ellipsoid with three axes (triaxial—— ) is used, usually for modeling the smaller, irregularly shaped moons and asteroid
) is used, usually for modeling the smaller, irregularly shaped moons and asteroid
s. The polar axis here is the same as the axis with the great moment of inertia and is approximately aligned with the rotational axis ( not the magnetic nor orbital pole). The geometric center of the ellipsoid is placed at the center of mass
of the body being modeled, and not the barycenter in a multi-body system.
In working with elliptic geometry, several parameters are commonly utilized, all of which are trigonometric function
s of an ellipse's angular eccentricity
, :
:
Due to rotational forces, the equatorial radius is usually larger than the polar radius. This ellipticity or flattening
, , determines how close to a true sphere
, determines how close to a true sphere
an oblate spheroid is, and is defined as

For Earth
, is around 1/300 (1/298.257223563 as a defined constant in WGS84), and is very gradually decreasing over geologic time scales. For comparison, Earth's Moon
is around 1/300 (1/298.257223563 as a defined constant in WGS84), and is very gradually decreasing over geologic time scales. For comparison, Earth's Moon
is even less elliptical, with a flattening of less than 1/825, while Jupiter
is visibly oblate at about 1/15 and one of Saturn's
triaxial moons, Telesto
, is nearly 1/3 to 1/2.
Such flattening is related to the eccentricity, , of the cross-sectional ellipse by
, of the cross-sectional ellipse by

It is traditional when defining a reference ellipsoid to specify the semi-major equatorial radius (usually in meters) and the inverse of the flattening ratio
(usually in meters) and the inverse of the flattening ratio  . The semi-minor polar radius is then easily derived.
. The semi-minor polar radius is then easily derived.
(north/south), longitude
(east/west), and elevation
(height).
For this purpose it is necessary to identify a zero meridian
, which for Earth is usually the Prime Meridian
. For other bodies a fixed surface feature is usually referenced, which for Mars is the meridian passing through the crater Airy-0
. It is possible for many different coordinate systems to be defined upon the same reference ellipsoid.
The longitude measures the rotational angle
between the zero meridian and the measured point. By convention for the Earth, Moon, and Sun it is expressed as degrees ranging from −180° to +180° For other bodies a range of 0° to 360° is used.
The latitude measures how close to the poles or equator a point is along a meridian, and is represented as angle from −90° to +90°, where 0° is the equator. The common or geodetic latitude is the angle between the equatorial plane and a line that is normal
to the reference ellipsoid. Depending on the flattening, it may be slightly different from the geocentric (geographic) latitude, which is the angle between the equatorial plane and a line from the center of the ellipsoid. For non-Earth bodies the terms planetographic and planetocentric are used instead.
The coordinates of a geodetic point are customarily stated as geodetic latitude and longitude, i.e., the direction in space of the geodetic normal containing the point, and the height h of the point over the reference ellipsoid. If these coordinates, i.e., latitude , longitude
, longitude  and height h, are given, one can compute the geocentric rectangular coordinates of the point as follows:
and height h, are given, one can compute the geocentric rectangular coordinates of the point as follows:
where
is the radius of curvature in the prime vertical
.
In contrast, extracting ,
,  and h from the rectangular coordinates usually requires iteration
and h from the rectangular coordinates usually requires iteration
:
Letting ,
,

Repeat until :
: 
Or, introducing the geocentric, , and parametric, or reduced,
, and parametric, or reduced,  , latitudes:
, latitudes:
 and
and  ,
,


Repeat until and
and  :
:

Traditional reference ellipsoids or geodetic datums are defined regionally and therefore non-geocentric, e.g., ED50
. Modern geodetic datums are established with
the aid of GPS and will therefore be geocentric, e.g., WGS 84.
The following table lists some of the most common ellipsoids:
and Mars
now have quite precise reference ellipsoids.
For rigid-surface nearly-spherical bodies, which includes all the rocky planets and many moons, ellipsoids are defined in terms of the axis of rotation and the mean surface height excluding any atmosphere. Mars is actually egg shaped
, where its north and south polar radii differ by approximately 6 km, however this difference is small enough that the average polar radius is used to define its ellipsoid. The Earth's Moon is effectively spherical, having no bulge at its equator. Where possible a fixed observable surface feature is used when defining a reference meridian.
For gaseous planets like Jupiter
, an effective surface for an ellipsoid is chosen as the equal-pressure boundary of one bar
. Since they have no permanent observable features the choices of prime meridians are made according to mathematical rules.
Small moons, asteroids, and comet nuclei frequently have irregular shapes. For some of these, such as Jupiter's Io
, a scalene (triaxial) ellipsoid is a better fit than the oblate spheroid. For highly irregular bodies the concept of a reference ellipsoid may have no useful value, so sometimes a spherical reference is used instead and points identified by planetocentric latitude and longitude. Even that can be problematic for non-convex
bodies, such as Eros
, in that latitude and longitude don't always uniquely identify a single surface location.
Geodesy
Geodesy , also named geodetics, a branch of earth sciences, is the scientific discipline that deals with the measurement and representation of the Earth, including its gravitational field, in a three-dimensional time-varying space. Geodesists also study geodynamical phenomena such as crustal...
, a reference ellipsoid is a mathematically-defined surface that approximates the geoid
Geoid
The geoid is that equipotential surface which would coincide exactly with the mean ocean surface of the Earth, if the oceans were in equilibrium, at rest , and extended through the continents . According to C.F...
, the truer figure of the Earth
Figure of the Earth
The expression figure of the Earth has various meanings in geodesy according to the way it is used and the precision with which the Earth's size and shape is to be defined. The actual topographic surface is most apparent with its variety of land forms and water areas. This is, in fact, the surface...
, or other planetary body.
Because of their relative simplicity, reference ellipsoids are used as a preferred surface on which geodetic network
Geodetic network
A geodetic network is a network of triangles which are measured exactly by techniques of terrestrial surveying or by satellite geodesy.In "classical geodesy" this is done by triangulation, based on measurements of angles and of some spare distances; the precise orientation to the geographic north...
computations are performed and point coordinates such as latitude
Latitude
In geography, the latitude of a location on the Earth is the angular distance of that location south or north of the Equator. The latitude is an angle, and is usually measured in degrees . The equator has a latitude of 0°, the North pole has a latitude of 90° north , and the South pole has a...
, longitude
Longitude
Longitude is a geographic coordinate that specifies the east-west position of a point on the Earth's surface. It is an angular measurement, usually expressed in degrees, minutes and seconds, and denoted by the Greek letter lambda ....
, and elevation
Elevation
The elevation of a geographic location is its height above a fixed reference point, most commonly a reference geoid, a mathematical model of the Earth's sea level as an equipotential gravitational surface ....
are defined.
Ellipsoid parameters
Mathematically, a reference ellipsoid is usually an oblate (flattened) spheroidSpheroid
A spheroid, or ellipsoid of revolution is a quadric surface obtained by rotating an ellipse about one of its principal axes; in other words, an ellipsoid with two equal semi-diameters....
with two different axes: An equator
Equator
An equator is the intersection of a sphere's surface with the plane perpendicular to the sphere's axis of rotation and containing the sphere's center of mass....
ial radius (the semi-major axis
Semi-major axis
The major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
 ), and a polar radius (the semi-minor axis
), and a polar radius (the semi-minor axisSemi-minor axis
In geometry, the semi-minor axis is a line segment associated with most conic sections . One end of the segment is the center of the conic section, and it is at right angles with the semi-major axis...
 ). More rarely, a scalene ellipsoid with three axes (triaxial——
). More rarely, a scalene ellipsoid with three axes (triaxial—— ) is used, usually for modeling the smaller, irregularly shaped moons and asteroid
) is used, usually for modeling the smaller, irregularly shaped moons and asteroidAsteroid
Asteroids are a class of small Solar System bodies in orbit around the Sun. They have also been called planetoids, especially the larger ones...
s. The polar axis here is the same as the axis with the great moment of inertia and is approximately aligned with the rotational axis ( not the magnetic nor orbital pole). The geometric center of the ellipsoid is placed at the center of mass
Center of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
of the body being modeled, and not the barycenter in a multi-body system.
In working with elliptic geometry, several parameters are commonly utilized, all of which are trigonometric function
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s of an ellipse's angular eccentricity
Angular eccentricity
In the study of ellipses and related geometry, various parameters in the distortion of a circle into an ellipse are identified and employed: Aspect ratio, flattening and eccentricity....
,
 :
:Due to rotational forces, the equatorial radius is usually larger than the polar radius. This ellipticity or flattening
Flattening
The flattening, ellipticity, or oblateness of an oblate spheroid is a measure of the "squashing" of the spheroid's pole, towards its equator...
,
 , determines how close to a true sphere
, determines how close to a true sphereSphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
an oblate spheroid is, and is defined as

For Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
,
 is around 1/300 (1/298.257223563 as a defined constant in WGS84), and is very gradually decreasing over geologic time scales. For comparison, Earth's Moon
is around 1/300 (1/298.257223563 as a defined constant in WGS84), and is very gradually decreasing over geologic time scales. For comparison, Earth's MoonMoon
The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
is even less elliptical, with a flattening of less than 1/825, while Jupiter
Jupiter
Jupiter is the fifth planet from the Sun and the largest planet within the Solar System. It is a gas giant with mass one-thousandth that of the Sun but is two and a half times the mass of all the other planets in our Solar System combined. Jupiter is classified as a gas giant along with Saturn,...
is visibly oblate at about 1/15 and one of Saturn's
Saturn
Saturn is the sixth planet from the Sun and the second largest planet in the Solar System, after Jupiter. Saturn is named after the Roman god Saturn, equated to the Greek Cronus , the Babylonian Ninurta and the Hindu Shani. Saturn's astronomical symbol represents the Roman god's sickle.Saturn,...
triaxial moons, Telesto
Telesto (moon)
Telesto is a moon of Saturn. It was discovered by Smith, Reitsema, Larson and Fountain in 1980 from ground-based observations, and was provisionally designated '. In the following months, several other apparitions were observed: , , and ....
, is nearly 1/3 to 1/2.
Such flattening is related to the eccentricity,
 , of the cross-sectional ellipse by
, of the cross-sectional ellipse by
It is traditional when defining a reference ellipsoid to specify the semi-major equatorial radius
 (usually in meters) and the inverse of the flattening ratio
(usually in meters) and the inverse of the flattening ratio  . The semi-minor polar radius is then easily derived.
. The semi-minor polar radius is then easily derived.Coordinates
A primary use of reference ellipsoids is to serve as a basis for a coordinate system of latitudeLatitude
In geography, the latitude of a location on the Earth is the angular distance of that location south or north of the Equator. The latitude is an angle, and is usually measured in degrees . The equator has a latitude of 0°, the North pole has a latitude of 90° north , and the South pole has a...
(north/south), longitude
Longitude
Longitude is a geographic coordinate that specifies the east-west position of a point on the Earth's surface. It is an angular measurement, usually expressed in degrees, minutes and seconds, and denoted by the Greek letter lambda ....
(east/west), and elevation
Elevation
The elevation of a geographic location is its height above a fixed reference point, most commonly a reference geoid, a mathematical model of the Earth's sea level as an equipotential gravitational surface ....
(height).
For this purpose it is necessary to identify a zero meridian
Meridian (geography)
A meridian is an imaginary line on the Earth's surface from the North Pole to the South Pole that connects all locations along it with a given longitude. The position of a point along the meridian is given by its latitude. Each meridian is perpendicular to all circles of latitude...
, which for Earth is usually the Prime Meridian
Prime Meridian
The Prime Meridian is the meridian at which the longitude is defined to be 0°.The Prime Meridian and its opposite the 180th meridian , which the International Date Line generally follows, form a great circle that divides the Earth into the Eastern and Western Hemispheres.An international...
. For other bodies a fixed surface feature is usually referenced, which for Mars is the meridian passing through the crater Airy-0
Airy-0
Airy-0 is a crater on Mars whose location defines the position of the prime meridian of that planet. It is about across and lies within the larger crater Airy in the region Sinus Meridiani....
. It is possible for many different coordinate systems to be defined upon the same reference ellipsoid.
The longitude measures the rotational angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
between the zero meridian and the measured point. By convention for the Earth, Moon, and Sun it is expressed as degrees ranging from −180° to +180° For other bodies a range of 0° to 360° is used.
The latitude measures how close to the poles or equator a point is along a meridian, and is represented as angle from −90° to +90°, where 0° is the equator. The common or geodetic latitude is the angle between the equatorial plane and a line that is normal
Surface normal
A surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...
to the reference ellipsoid. Depending on the flattening, it may be slightly different from the geocentric (geographic) latitude, which is the angle between the equatorial plane and a line from the center of the ellipsoid. For non-Earth bodies the terms planetographic and planetocentric are used instead.
The coordinates of a geodetic point are customarily stated as geodetic latitude and longitude, i.e., the direction in space of the geodetic normal containing the point, and the height h of the point over the reference ellipsoid. If these coordinates, i.e., latitude
 , longitude
, longitude  and height h, are given, one can compute the geocentric rectangular coordinates of the point as follows:
and height h, are given, one can compute the geocentric rectangular coordinates of the point as follows:where

is the radius of curvature in the prime vertical
Prime vertical
In astronomy and astrology, the prime vertical is the vertical circle passing east and west through the zenith, and intersecting the horizon in its east and west points....
.
In contrast, extracting
 ,
,  and h from the rectangular coordinates usually requires iteration
and h from the rectangular coordinates usually requires iterationIterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
:
Letting
 ,
,
Repeat until
 :
: 
Or, introducing the geocentric,
 , and parametric, or reduced,
, and parametric, or reduced,  , latitudes:
, latitudes: and
and  ,
,

Repeat until
 and
and  :
:
- Once
 is determined, then h can be isolated:
is determined, then h can be isolated:
- In contrast, as
 cancels out,
cancels out,  is a simple extraction from
is a simple extraction from  and
and  :
:
- Note that the above formula for longitude is only valid, within one semi-circle (E.G. -Pi/2 to +pi/2), use of a two argument version of arctan is recommended.
Historical Earth ellipsoids
Currently the most common reference ellipsoid used, and that used in the context of the Global Positioning System, is the one defined by WGS 84.Traditional reference ellipsoids or geodetic datums are defined regionally and therefore non-geocentric, e.g., ED50
ED50
ED 50 is a geodetic datum which was defined after World War II for the international connection of geodetic networks....
. Modern geodetic datums are established with
the aid of GPS and will therefore be geocentric, e.g., WGS 84.
The following table lists some of the most common ellipsoids:
| Name | Equatorial axis (m Metre The metre , symbol m, is the base unit of length in the International System of Units . Originally intended to be one ten-millionth of the distance from the Earth's equator to the North Pole , its definition has been periodically refined to reflect growing knowledge of metrology... ) | Polar axis (m) | Inverse flattening, |
|---|---|---|---|
| Airy George Biddell Airy Sir George Biddell Airy PRS KCB was an English mathematician and astronomer, Astronomer Royal from 1835 to 1881... 1830 |
6 377 563.4 | 6 356 256.9 | 299.324 975 3 |
| Clarke 1866 | 6 378 206.4 | 6 356 583.8 | 294.978 698 2 |
| Bessel 1841 Bessel ellipsoid The Bessel ellipsoid is an important reference ellipsoid of geodesy. It is currently used by several countries for their national geodetic surveys, in Europe and on other continents, but will be replaced in the next decades by modern ellipsoids of satellite geodesy.The Bessel ellipsoid was derived... |
6 377 397.155 | 6 356 078.965 | 299.152 843 4 |
| International 1924 | 6 378 388 | 6 356 911.9 | 297 |
| Krasovsky 1940 SK-42 Reference System The SK-42 reference system also known as the Krasovsky ellipsoid, is a coordinate system established in the Soviet Union in 1942 as Systema koordinat , and provides parameters which are linked to the geocentric Cartesian coordinate system PZ-90... |
6 378 245 | 6 356 863 | 298.299 738 1 |
| GRS 1980 GRS 80 GRS 80, or Geodetic Reference System 1980, is a geodetic reference system consisting of a global reference ellipsoid and a gravity field model.-Geodesy:... |
6 378 137 | 6 356 752.3141 | 298.257 222 101 |
| WGS 1984 | 6 378 137 | 6 356 752.3142 | 298.257 223 563 |
| Sphere (6371 km) | 6 371 000 | 6 371 000 |  |
Ellipsoids for other planetary bodies
Reference ellipsoids are also useful for geodetic mapping of other planetary bodies including planets, their satellites, asteroids and comet nuclei. Some well observed bodies such as the MoonMoon
The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
and Mars
Mars
Mars is the fourth planet from the Sun in the Solar System. The planet is named after the Roman god of war, Mars. It is often described as the "Red Planet", as the iron oxide prevalent on its surface gives it a reddish appearance...
now have quite precise reference ellipsoids.
For rigid-surface nearly-spherical bodies, which includes all the rocky planets and many moons, ellipsoids are defined in terms of the axis of rotation and the mean surface height excluding any atmosphere. Mars is actually egg shaped
Oval (geometry)
In technical drawing, an oval is a figure constructed from two pairs of arcs, with two different radii . The arcs are joined at a point, in which lines tangential to both joining arcs lie on the same line, thus making the joint smooth...
, where its north and south polar radii differ by approximately 6 km, however this difference is small enough that the average polar radius is used to define its ellipsoid. The Earth's Moon is effectively spherical, having no bulge at its equator. Where possible a fixed observable surface feature is used when defining a reference meridian.
For gaseous planets like Jupiter
Jupiter
Jupiter is the fifth planet from the Sun and the largest planet within the Solar System. It is a gas giant with mass one-thousandth that of the Sun but is two and a half times the mass of all the other planets in our Solar System combined. Jupiter is classified as a gas giant along with Saturn,...
, an effective surface for an ellipsoid is chosen as the equal-pressure boundary of one bar
Bar (unit)
The bar is a unit of pressure equal to 100 kilopascals, and roughly equal to the atmospheric pressure on Earth at sea level. Other units derived from the bar are the megabar , kilobar , decibar , centibar , and millibar...
. Since they have no permanent observable features the choices of prime meridians are made according to mathematical rules.
Small moons, asteroids, and comet nuclei frequently have irregular shapes. For some of these, such as Jupiter's Io
Io (moon)
Io ) is the innermost of the four Galilean moons of the planet Jupiter and, with a diameter of , the fourth-largest moon in the Solar System. It was named after the mythological character of Io, a priestess of Hera who became one of the lovers of Zeus....
, a scalene (triaxial) ellipsoid is a better fit than the oblate spheroid. For highly irregular bodies the concept of a reference ellipsoid may have no useful value, so sometimes a spherical reference is used instead and points identified by planetocentric latitude and longitude. Even that can be problematic for non-convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
bodies, such as Eros
433 Eros
433 Eros is a near-Earth asteroid discovered in 1898, and the first asteroid to be orbited by a probe . It is an S-type asteroid approximately 34.4×11.2×11.2 km in size, the second-largest NEA after 1036 Ganymed, and belongs to the Amor group.Eros is a Mars-crosser asteroid, the first known...
, in that latitude and longitude don't always uniquely identify a single surface location.
See also
- Earth ellipsoidEarth ellipsoidAn Earth ellipsoid is a mathematical figure approximating the shape of the Earth, used as a reference frame for computations in geodesy, astronomy and the geosciences...
- Earth radiusEarth radiusBecause the Earth is not perfectly spherical, no single value serves as its natural radius. Distances from points on the surface to the center range from 6,353 km to 6,384 km...
- Figure of the EarthFigure of the EarthThe expression figure of the Earth has various meanings in geodesy according to the way it is used and the precision with which the Earth's size and shape is to be defined. The actual topographic surface is most apparent with its variety of land forms and water areas. This is, in fact, the surface...
- GeoidGeoidThe geoid is that equipotential surface which would coincide exactly with the mean ocean surface of the Earth, if the oceans were in equilibrium, at rest , and extended through the continents . According to C.F...
- Meridian arcMeridian arcIn geodesy, a meridian arc measurement is a highly accurate determination of the distance between two points with the same longitude. Two or more such determinations at different locations then specify the shape of the reference ellipsoid which best approximates the shape of the geoid. This...