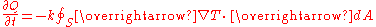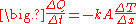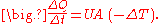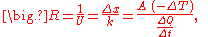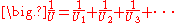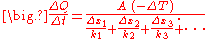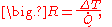Heat conduction
Encyclopedia
In heat transfer
, conduction (or heat conduction) is a mode of transfer of energy
within and between bodies of matter, due to a temperature gradient
. Conduction means collisional and diffusive transfer of kinetic energy of particles of ponderable matter (as distinct from photons). Conduction takes place in all forms of ponderable matter, viz. solids, liquids, gases and plasmas. Heat spontaneously tends to flow from a body at a higher temperature to a body at a lower temperature. In the absence of external driving fluxes, temperature differences, over time, approach thermal equilibrium
.
In conduction, the heat flows through the body itself, as opposed to its transfer by the bulk motion of the matter as in convection
, and by thermal radiation
. In solids, it is due to the combination of vibrations of the molecules in a lattice
or phonons with the energy transported by free electrons
. In gases and liquids, conduction is due to the collisions and diffusion of the molecules during their random motion. Photons in general do not collide with one another and thermal transport by electromagnetic radiation
is not regarded as conduction of heat. In solids, it is not simple to separate transfer by photons from transfer by ponderable matter, but the distinction can be more easily made in liquids, and is routinely made in gases.
In the engineering sciences, heat transfer includes the processes of thermal radiation
, convection
, and sometimes mass transfer and often more than one of these processes occurs in a given situation.
s interact with neighboring particles, transferring some of their kinetic energy. Heat is transferred by conduction when adjacent atoms vibrate against one another, or as electrons move from one atom to another. Conduction is the most significant means of heat transfer within a solid or between solid objects in thermal contact
. Conduction is greater in solids because the network of relatively fixed spatial relationships between atoms helps to transfer energy between them by vibration.
As density
decreases so does conduction. Therefore, fluids (and especially gases) are less conductive. This is due to the large distance between atoms in a gas: fewer collisions between atoms means less conduction. Conductivity of gases increases with temperature. Conductivity increases with increasing pressure from vacuum up to a critical point that the density of the gas is such that molecules of the gas may be expected to collide with each other before they transfer heat from one surface to another. After this point conductivity increases only slightly with increasing pressure and density.
Thermal contact conductance
is the study of heat conduction between solid bodies in contact. A temperature drop is often observed at the interface between the two surfaces in contact. This phenomenon is said to be a result of a thermal contact resistance existing between the contacting surfaces. Interfacial thermal resistance
is a measure of an interface's resistance to thermal flow. This thermal resistance differs from contact resistance, as it exists even at atomically perfect interfaces. Understanding the thermal resistance at the interface between two materials is of primary significance in the study of its thermal properties. Interfaces often contribute significantly to the observed properties of the materials.
The inter-molecular transfer of energy could be primarily by elastic impact as in fluids or by free electron diffusion as in metals or phonon vibration
as in insulators. In insulators
the heat flux is carried almost entirely by phonon
vibrations.
Metals (e.g. copper, platinum, gold,etc.) are usually the best conductors
of thermal energy. This is due to the way that metals are chemically bonded: metallic bond
s (as opposed to covalent or ionic bonds) have free-moving electrons which are able to transfer thermal energy rapidly through the metal. The "electron fluid" of a conductive
metallic solid conducts nearly all of the heat flux through the solid. Phonon flux is still present, but carries less than 1% of the energy. Electrons also conduct electric current
through conductive solids, and the thermal
and electrical conductivities of most metal
s have about the same ratio. A good electrical conductor, such as copper
, usually also conducts heat well. The Peltier-Seebeck effect exhibits the propensity of electrons to conduct heat through an electrically conductive solid. Thermoelectricity is caused by the relationship between electrons, heat fluxes and electrical currents.
Heat conduction within a solid is directly analogous to diffusion
of particles within a fluid, in the situation where there are no fluid currents.
To quantify the ease with which a particular medium conducts, engineers employ the thermal conductivity
, also known as the conductivity constant or conduction coefficient, k. In thermal conductivity
k is defined as "the quantity of heat, Q, transmitted in time (t) through a thickness (L), in a direction normal to a surface of area (A), due to a temperature difference (ΔT) [...]." Thermal conductivity is a material property
that is primarily dependent on the medium's phase, temperature, density, and molecular bonding. Thermal effusivity is a quantity derived from conductivity which is a measure of its ability to exchange thermal energy with its surroundings.
For example, a bar may be cold at one end and hot at the other, but after a state of steady state conduction is reached, the spatial gradient of temperatures along the bar does not change any further, as time proceeds. Instead, the temperature at any given section of the rod remains constant, and this temperature varies linearly in space, along the direction of heat transfer.
In steady state conduction, all the laws of direct current electrical conduction can be applied to "heat currents". In such cases, it is possible to take "thermal resistances" as the analog to electrical resistances. In such cases, temperature plays the role of voltage, and heat transferred per unit time (heat power) is the analog of electrical current. Steady state systems can be modelled by networks of such thermal resistances in series and in parallel, in exact analogy to electrical networks of resistors. See purely resistive thermal circuits for an example of such a network.
When a new perturbation of temperature of this type happens, temperatures within the system will change in time toward a new equilibrium with the new conditions, provided that these do not change. After equilibrium, heat flow into the system will once again equal the heat flow out, and temperatures at each point inside the system no longer change. Once this happens, transient conduction is ended, although steady-state conduction may continue if there continues to be heat flow.
If changes in external temperatures or internal heat generation changes are too rapid for equilibrium of temperatures in space to take place, then the system never reaches a state of unchaging temperature distribution in time, and the system remains in a transient state.
An example of a new source of heat "turning on" within an object which causes transient conduction, is an engine starting in an automobile. In this case the transient thermal conduction phase for the entire machine would be over, and the steady state phase would appear, as soon as the engine had reached steady-state operating temperature. In this state of steady-state equilibrium, temperatures would vary greatly from the engine cylinders to other parts of the automobile, but at no point in space within the automobile would temperature be increasing or decreasing. After establishment of this state, the transient conduction phase of heat transfer would be over.
New external conditions also cause this process: for example the copper bar in the example steady-state conduction would experience transient conduction as soon as one end was subjected to a different temperature from the other. Over time, the field of temperatures inside the bar would reach a new steady-state, in which a constant temperature gradient along the bar will finally be set up, and this gradient would then stay constant in space. Typically, such a new steady state gradient is approached exponentially with time after a new temperature-or-heat source or sink, has been introduced. When a "transient conduction" phase is over, heat flow may still continue at high power, so long as temperatures do not change.
An example of transient conduction which does not end with steady-state conduction, but rather no conduction, occurs when a hot copper ball is dropped into oil at a low temperature. Here the temperature field within the object begins to change as a function of time, as the heat is removed from the metal, and the interest lies in analyzing this spatial change of temperature within the object over time, until all gradients disappear entirely (the ball has reached the same temperature as the oil). Mathematically, this condition is also approached exponentially; in theory it takes infinite time, but in practice it is over, for all intents and purposes, in a much shorter period. At the end of this process with no heat sink but the internal parts of the ball (which are finite), there is no steady state heat conduction to be reached. Such a state never occurs in this situation, but rather the end of the process is when there is no heat conduction at all.
Analysis of non steady-state conduction systems is more complex than steady-state systems, and (except for simple shapes) calls for the application of approximation theories, and/or numerical analysis by computer. One popular graphical method involves the use of Heisler Chart
s.
Occasionally transient conduction problems may be considerably simplified if regions of the object being heated or cooled can be identified, in which thermal conductivity
is very much greater than than that for heat paths leading into the region. In this case, the region with high conductivity can often be treated in the lumped capacitance model
, as a "lump" of material with a simple thermal capacitance consisting of its aggregate heat capacity
. Such regions show no temperature variation across their extent during warming or cooling (as compared to the rest of the system) due to their far higher conductance. During transient conduction, therefore, their temperature changes uniformly in space, and as a simple exponential in time. An example of such systems are those which follow "Newton's law of cooling" during transient cooling (or the reverse during heating). The equivalent thermal circuit consists of a simple capacitor in series with a resistor. In such cases, the remainder of the system with high thermal resistance (comparatively low conductivity) plays the role of the resistor in the circuit.
is a model that is compatible with the theory of special relativity. For most of the last century, it was recognized that Fourier equation is in contradiction with the theory of relativity because it admits an infinite speed of propagation of heat signals. For example, according to Fourier equation, a pulse of heat at the origin would be felt at infinity instantaneously. The speed of information propagation is faster than the speed of light in vacuum, which is physically inadmissible within the framework of relativity. Alterations to the Fourier model provided for a relativistic model of heat conduction, avoiding this problem.
is a quantum mechanical phenomenon in which heat transfer
occurs by wave
-like motion, rather than by the more usual mechanism of diffusion
. Heat takes the place of pressure in normal sound waves. This leads to a very high thermal conductivity
. It is known as "second sound" because the wave motion of heat is similar to the propagation of sound
in air.
's law, states that the time rate of heat transfer
through a material is proportional
to the negative gradient
in the temperature and to the area, at right angles to that gradient, through which the heat is flowing. We can state this law in two equivalent forms: the integral form, in which we look at the amount of energy flowing into or out of a body as a whole, and the differential form, in which we look at the flow rates or fluxes
of energy locally.
Newton's law of cooling is a discrete analog of Fourier's law, while Ohm's law
is the electrical analogue of Fourier's law.
density,
, is equal to the product of thermal conductivity, 
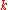, and the negative local temperature gradient, 
. The heat flux density is the amount of energy that flows through a unit area per unit time.
where (including the SI
units)
The thermal conductivity,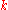
, is often treated as a constant, though this is not always true. While the thermal conductivity of a material generally varies with temperature, the variation can be small over a significant range of temperatures for some common materials. In anisotropic materials, the thermal conductivity typically varies with orientation; in this case 
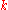is represented by a second-order tensor
. In nonuniform materials,
varies with spatial location.
For many simple applications, Fourier's law is used in its one-dimensional form. In the x-direction,
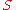, we arrive at the integral form of Fourier's law:
where (including the SI
units)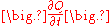
is the amount of heat transferred per unit time (in W) and
The above differential equation
, when integrated
for a homogeneous material of 1-D geometry between two endpoints at constant temperature, gives the heat flow rate as:
where
This law forms the basis for the derivation of the heat equation
.
where U is the conductance, in W/(m2 K).
Fourier's law can also be stated as:
The reciprocal of conductance is resistance, R, given by:
and it is resistance which is additive when several conducting layers lie between the hot and cool regions, because A and Q are the same for all layers. In a multilayer partition, the total conductance is related to the conductance of its layers by:
So, when dealing with a multilayer partition, the following formula is usually used:
When heat is being conducted from one fluid to another through a barrier, it is sometimes important to consider the conductance of the thin film
of fluid which remains stationary next to the barrier. This thin film of fluid is difficult to quantify, its characteristics depending upon complex conditions of turbulence
and viscosity
, but when dealing with thin high-conductance barriers it can sometimes be quite significant.
, can be reformulated in terms of intensive properties
.
Ideally, the formulae for conductance should produce a quantity with dimensions independent of distance, like Ohm's Law
for electrical resistance: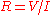
, and conductance: 
.
From the electrical formula: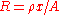
, where ρ is resistivity, x = length, and A is cross-sectional area, we have 
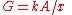, where G is conductance, k is conductivity, x = length, and A = cross-sectional area.
For Heat,
where U is the conductance.
Fourier's law can also be stated as:
analogous to Ohm's law: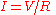
or 
The reciprocal of conductance is resistance, R, given by:
analogous to Ohm's law: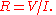
The rules for combining resistances and conductances (in series and in parallel) are the same for both heat flow and electric current.
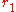, the external radius 
, and the length denoted as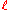 
.
The temperature difference between the inner and outer wall can be expressed as
.
The area of the heat flow:
When Fourier’s equation is applied:
Rearranged:
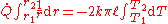
Therefore the rate of heat transfer is
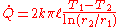
The thermal resistance is
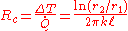
And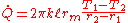
, where 
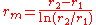and it is important to note that this is the log-mean radius.
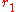, the external radius 
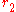of a spherical shell,
The surface area
of a sphere is given by the following formula
and solve rest of the spherical part as we solved for cylindrical shell(see above topic).
and finally we get
is directly focused on the idea of conduction of heat. Bailyn (1994) writes that "... the zeroth law may be stated:
A diathermal wall is a connection of contiguity between two bodies that allows the passage of heat by conduction between them.
This statement of the 'zeroth law' belongs to an idealized theoretical discourse, and actual physical walls do not match its grandiloquent generality.
But with suitable restrictions, the statement has physical import. For example, the material of the wall must not suffer a phase transition, such as evaporation or fusion, at the temperature at which it has to conduct heat. But when only thermal equilibrium is being considered, and time is not urgent, so that the conductivity of the material does not matter too much, one suitable conductor of heat is as good as another. Conversely, another aspect of the zeroth law is that, subject again to suitable restrictions, a given diathermal wall is indifferent to the nature of the heat bath to which it is connected. For example the glass bulb of a thermometer will act as a diathermal wall whether exposed to a gas or to a liquid, provided they do not corrode it or melt it.
These indifferences are amongst the defining characteristics of heat transfer
. In a sense they are symmetries of heat transfer.
Heat transfer
Heat transfer is a discipline of thermal engineering that concerns the exchange of thermal energy from one physical system to another. Heat transfer is classified into various mechanisms, such as heat conduction, convection, thermal radiation, and phase-change transfer...
, conduction (or heat conduction) is a mode of transfer of energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
within and between bodies of matter, due to a temperature gradient
Temperature gradient
A temperature gradient is a physical quantity that describes in which direction and at what rate the temperature changes the most rapidly around a particular location. The temperature gradient is a dimensional quantity expressed in units of degrees per unit length...
. Conduction means collisional and diffusive transfer of kinetic energy of particles of ponderable matter (as distinct from photons). Conduction takes place in all forms of ponderable matter, viz. solids, liquids, gases and plasmas. Heat spontaneously tends to flow from a body at a higher temperature to a body at a lower temperature. In the absence of external driving fluxes, temperature differences, over time, approach thermal equilibrium
Thermal equilibrium
Thermal equilibrium is a theoretical physical concept, used especially in theoretical texts, that means that all temperatures of interest are unchanging in time and uniform in space...
.
In conduction, the heat flows through the body itself, as opposed to its transfer by the bulk motion of the matter as in convection
Convection
Convection is the movement of molecules within fluids and rheids. It cannot take place in solids, since neither bulk current flows nor significant diffusion can take place in solids....
, and by thermal radiation
Thermal radiation
Thermal radiation is electromagnetic radiation generated by the thermal motion of charged particles in matter. All matter with a temperature greater than absolute zero emits thermal radiation....
. In solids, it is due to the combination of vibrations of the molecules in a lattice
Crystal structure
In mineralogy and crystallography, crystal structure is a unique arrangement of atoms or molecules in a crystalline liquid or solid. A crystal structure is composed of a pattern, a set of atoms arranged in a particular way, and a lattice exhibiting long-range order and symmetry...
or phonons with the energy transported by free electrons
Free electron model
In solid-state physics, the free electron model is a simple model for the behaviour of valence electrons in a crystal structure of a metallic solid. It was developed principally by Arnold Sommerfeld who combined the classical Drude model with quantum mechanical Fermi-Dirac statistics and hence it...
. In gases and liquids, conduction is due to the collisions and diffusion of the molecules during their random motion. Photons in general do not collide with one another and thermal transport by electromagnetic radiation
Electromagnetic radiation
Electromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
is not regarded as conduction of heat. In solids, it is not simple to separate transfer by photons from transfer by ponderable matter, but the distinction can be more easily made in liquids, and is routinely made in gases.
In the engineering sciences, heat transfer includes the processes of thermal radiation
Thermal radiation
Thermal radiation is electromagnetic radiation generated by the thermal motion of charged particles in matter. All matter with a temperature greater than absolute zero emits thermal radiation....
, convection
Convection
Convection is the movement of molecules within fluids and rheids. It cannot take place in solids, since neither bulk current flows nor significant diffusion can take place in solids....
, and sometimes mass transfer and often more than one of these processes occurs in a given situation.
Overview
On a microscopic scale, conduction occurs as rapidly moving or vibrating atoms and moleculeMolecule
A molecule is an electrically neutral group of at least two atoms held together by covalent chemical bonds. Molecules are distinguished from ions by their electrical charge...
s interact with neighboring particles, transferring some of their kinetic energy. Heat is transferred by conduction when adjacent atoms vibrate against one another, or as electrons move from one atom to another. Conduction is the most significant means of heat transfer within a solid or between solid objects in thermal contact
Thermal contact
In heat transfer and thermodynamics, a thermodynamic system is said to be in thermal contact with another system if it can exchange energy with it through the process of heat...
. Conduction is greater in solids because the network of relatively fixed spatial relationships between atoms helps to transfer energy between them by vibration.
As density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
decreases so does conduction. Therefore, fluids (and especially gases) are less conductive. This is due to the large distance between atoms in a gas: fewer collisions between atoms means less conduction. Conductivity of gases increases with temperature. Conductivity increases with increasing pressure from vacuum up to a critical point that the density of the gas is such that molecules of the gas may be expected to collide with each other before they transfer heat from one surface to another. After this point conductivity increases only slightly with increasing pressure and density.
Thermal contact conductance
Thermal contact conductance
In physics, thermal contact conductance is the study of heat conduction between solid bodies in thermal contact. The thermal contact conductance coefficient, h_c, is a property indicating the thermal conductivity, or ability to conduct heat, between two bodies in contact...
is the study of heat conduction between solid bodies in contact. A temperature drop is often observed at the interface between the two surfaces in contact. This phenomenon is said to be a result of a thermal contact resistance existing between the contacting surfaces. Interfacial thermal resistance
Interfacial thermal resistance
Interfacial thermal resistance, also known as thermal boundary resistance, or Kapitza resistance, is a measure of an interface's resistance to thermal flow. This thermal resistance differs from contact resistance, as it exists even at atomically perfect interfaces...
is a measure of an interface's resistance to thermal flow. This thermal resistance differs from contact resistance, as it exists even at atomically perfect interfaces. Understanding the thermal resistance at the interface between two materials is of primary significance in the study of its thermal properties. Interfaces often contribute significantly to the observed properties of the materials.
The inter-molecular transfer of energy could be primarily by elastic impact as in fluids or by free electron diffusion as in metals or phonon vibration
Phonon
In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, such as solids and some liquids...
as in insulators. In insulators
Thermal insulation
Thermal insulation is the reduction of the effects of the various processes of heat transfer between objects in thermal contact or in range of radiative influence. Heat transfer is the transfer of thermal energy between objects of differing temperature...
the heat flux is carried almost entirely by phonon
Phonon
In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, such as solids and some liquids...
vibrations.
Metals (e.g. copper, platinum, gold,etc.) are usually the best conductors
Heat conduction
In heat transfer, conduction is a mode of transfer of energy within and between bodies of matter, due to a temperature gradient. Conduction means collisional and diffusive transfer of kinetic energy of particles of ponderable matter . Conduction takes place in all forms of ponderable matter, viz....
of thermal energy. This is due to the way that metals are chemically bonded: metallic bond
Metallic bond
Metallic bonding is the electrostatic attractive forces between the delocalized electrons, called conduction electrons, gathered in an "electron sea", and the positively charged metal ions...
s (as opposed to covalent or ionic bonds) have free-moving electrons which are able to transfer thermal energy rapidly through the metal. The "electron fluid" of a conductive
Electrical conductor
In physics and electrical engineering, a conductor is a material which contains movable electric charges. In metallic conductors such as copper or aluminum, the movable charged particles are electrons...
metallic solid conducts nearly all of the heat flux through the solid. Phonon flux is still present, but carries less than 1% of the energy. Electrons also conduct electric current
Electric current
Electric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire...
through conductive solids, and the thermal
Thermal conductivity
In physics, thermal conductivity, k, is the property of a material's ability to conduct heat. It appears primarily in Fourier's Law for heat conduction....
and electrical conductivities of most metal
Metal
A metal , is an element, compound, or alloy that is a good conductor of both electricity and heat. Metals are usually malleable and shiny, that is they reflect most of incident light...
s have about the same ratio. A good electrical conductor, such as copper
Copper
Copper is a chemical element with the symbol Cu and atomic number 29. It is a ductile metal with very high thermal and electrical conductivity. Pure copper is soft and malleable; an exposed surface has a reddish-orange tarnish...
, usually also conducts heat well. The Peltier-Seebeck effect exhibits the propensity of electrons to conduct heat through an electrically conductive solid. Thermoelectricity is caused by the relationship between electrons, heat fluxes and electrical currents.
Heat conduction within a solid is directly analogous to diffusion
Diffusion
Molecular diffusion, often called simply diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size of the particles...
of particles within a fluid, in the situation where there are no fluid currents.
To quantify the ease with which a particular medium conducts, engineers employ the thermal conductivity
Thermal conductivity
In physics, thermal conductivity, k, is the property of a material's ability to conduct heat. It appears primarily in Fourier's Law for heat conduction....
, also known as the conductivity constant or conduction coefficient, k. In thermal conductivity
Thermal conductivity
In physics, thermal conductivity, k, is the property of a material's ability to conduct heat. It appears primarily in Fourier's Law for heat conduction....
k is defined as "the quantity of heat, Q, transmitted in time (t) through a thickness (L), in a direction normal to a surface of area (A), due to a temperature difference (ΔT) [...]." Thermal conductivity is a material property
Physical property
A physical property is any property that is measurable whose value describes a physical system's state. The changes in the physical properties of a system can be used to describe its transformations ....
that is primarily dependent on the medium's phase, temperature, density, and molecular bonding. Thermal effusivity is a quantity derived from conductivity which is a measure of its ability to exchange thermal energy with its surroundings.
Steady-state conduction
Steady state conduction is the form of conduction that happens when the temperature difference(s) driving the conduction are constant, so that (after an equilibration time), the spatial distribution of temperatures (temperature field) in the conducting object does not change any further. Thus, all partial derivatives of temperature with respect to space may either be zero or have nonzero values, but all derivatives of temperature at any point with respect to time are uniformly zero. In steady state conduction, the amount of heat entering any region of an object is equal to amount of heat coming out (if this were not so, the temperature would be rising or falling, as thermal energy was tapped or trapped in a region).For example, a bar may be cold at one end and hot at the other, but after a state of steady state conduction is reached, the spatial gradient of temperatures along the bar does not change any further, as time proceeds. Instead, the temperature at any given section of the rod remains constant, and this temperature varies linearly in space, along the direction of heat transfer.
In steady state conduction, all the laws of direct current electrical conduction can be applied to "heat currents". In such cases, it is possible to take "thermal resistances" as the analog to electrical resistances. In such cases, temperature plays the role of voltage, and heat transferred per unit time (heat power) is the analog of electrical current. Steady state systems can be modelled by networks of such thermal resistances in series and in parallel, in exact analogy to electrical networks of resistors. See purely resistive thermal circuits for an example of such a network.
Transient conduction
In general, during any period in which temperatures are changing in time at any place within an object, the mode of thermal energy flow is termed transient conduction. Another term is "non steady-state" conduction, referring to time-dependence of temperature fields in an object. Non-steady-state situations appear after an imposed change in temperature at a boundary of an object. They may also occur with temperature changes inside an object, as a result of a new source or sink of heat suddenly introduced within an object, causing temperatures near the source or sink to change in time.When a new perturbation of temperature of this type happens, temperatures within the system will change in time toward a new equilibrium with the new conditions, provided that these do not change. After equilibrium, heat flow into the system will once again equal the heat flow out, and temperatures at each point inside the system no longer change. Once this happens, transient conduction is ended, although steady-state conduction may continue if there continues to be heat flow.
If changes in external temperatures or internal heat generation changes are too rapid for equilibrium of temperatures in space to take place, then the system never reaches a state of unchaging temperature distribution in time, and the system remains in a transient state.
An example of a new source of heat "turning on" within an object which causes transient conduction, is an engine starting in an automobile. In this case the transient thermal conduction phase for the entire machine would be over, and the steady state phase would appear, as soon as the engine had reached steady-state operating temperature. In this state of steady-state equilibrium, temperatures would vary greatly from the engine cylinders to other parts of the automobile, but at no point in space within the automobile would temperature be increasing or decreasing. After establishment of this state, the transient conduction phase of heat transfer would be over.
New external conditions also cause this process: for example the copper bar in the example steady-state conduction would experience transient conduction as soon as one end was subjected to a different temperature from the other. Over time, the field of temperatures inside the bar would reach a new steady-state, in which a constant temperature gradient along the bar will finally be set up, and this gradient would then stay constant in space. Typically, such a new steady state gradient is approached exponentially with time after a new temperature-or-heat source or sink, has been introduced. When a "transient conduction" phase is over, heat flow may still continue at high power, so long as temperatures do not change.
An example of transient conduction which does not end with steady-state conduction, but rather no conduction, occurs when a hot copper ball is dropped into oil at a low temperature. Here the temperature field within the object begins to change as a function of time, as the heat is removed from the metal, and the interest lies in analyzing this spatial change of temperature within the object over time, until all gradients disappear entirely (the ball has reached the same temperature as the oil). Mathematically, this condition is also approached exponentially; in theory it takes infinite time, but in practice it is over, for all intents and purposes, in a much shorter period. At the end of this process with no heat sink but the internal parts of the ball (which are finite), there is no steady state heat conduction to be reached. Such a state never occurs in this situation, but rather the end of the process is when there is no heat conduction at all.
Analysis of non steady-state conduction systems is more complex than steady-state systems, and (except for simple shapes) calls for the application of approximation theories, and/or numerical analysis by computer. One popular graphical method involves the use of Heisler Chart
Heisler Chart
Heisler Charts are a set of two charts per included geometry introduced in 1947 by M. P. Heisler which were supplemented by a third chart per geometry in 1961 by H. Gröber...
s.
Occasionally transient conduction problems may be considerably simplified if regions of the object being heated or cooled can be identified, in which thermal conductivity
Thermal conductivity
In physics, thermal conductivity, k, is the property of a material's ability to conduct heat. It appears primarily in Fourier's Law for heat conduction....
is very much greater than than that for heat paths leading into the region. In this case, the region with high conductivity can often be treated in the lumped capacitance model
Lumped capacitance model
A lumped capacitance model, also called lumped system analysis, reduces a thermal system to a number of discrete “lumps” and assumes that the temperature difference inside each lump is negligible. This approximation is useful to simplify otherwise complex differential heat equations...
, as a "lump" of material with a simple thermal capacitance consisting of its aggregate heat capacity
Heat capacity
Heat capacity , or thermal capacity, is the measurable physical quantity that characterizes the amount of heat required to change a substance's temperature by a given amount...
. Such regions show no temperature variation across their extent during warming or cooling (as compared to the rest of the system) due to their far higher conductance. During transient conduction, therefore, their temperature changes uniformly in space, and as a simple exponential in time. An example of such systems are those which follow "Newton's law of cooling" during transient cooling (or the reverse during heating). The equivalent thermal circuit consists of a simple capacitor in series with a resistor. In such cases, the remainder of the system with high thermal resistance (comparatively low conductivity) plays the role of the resistor in the circuit.
Relativistic conduction
The theory of relativistic heat conductionRelativistic heat conduction
The theory of relativistic heat conduction claims to be the only model for heat conduction that is compatible with the theory of special relativity, the second law of thermodynamics, electrodynamics, and quantum mechanics, simultaneously...
is a model that is compatible with the theory of special relativity. For most of the last century, it was recognized that Fourier equation is in contradiction with the theory of relativity because it admits an infinite speed of propagation of heat signals. For example, according to Fourier equation, a pulse of heat at the origin would be felt at infinity instantaneously. The speed of information propagation is faster than the speed of light in vacuum, which is physically inadmissible within the framework of relativity. Alterations to the Fourier model provided for a relativistic model of heat conduction, avoiding this problem.
Quantum conduction
Second soundSecond sound
Second sound is a quantum mechanical phenomenon in which heat transfer occurs by wave-like motion, rather than by the more usual mechanism of diffusion. Heat takes the place of pressure in normal sound waves. This leads to a very high thermal conductivity...
is a quantum mechanical phenomenon in which heat transfer
Heat transfer
Heat transfer is a discipline of thermal engineering that concerns the exchange of thermal energy from one physical system to another. Heat transfer is classified into various mechanisms, such as heat conduction, convection, thermal radiation, and phase-change transfer...
occurs by wave
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
-like motion, rather than by the more usual mechanism of diffusion
Diffusion
Molecular diffusion, often called simply diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size of the particles...
. Heat takes the place of pressure in normal sound waves. This leads to a very high thermal conductivity
Thermal conductivity
In physics, thermal conductivity, k, is the property of a material's ability to conduct heat. It appears primarily in Fourier's Law for heat conduction....
. It is known as "second sound" because the wave motion of heat is similar to the propagation of sound
Sound
Sound is a mechanical wave that is an oscillation of pressure transmitted through a solid, liquid, or gas, composed of frequencies within the range of hearing and of a level sufficiently strong to be heard, or the sensation stimulated in organs of hearing by such vibrations.-Propagation of...
in air.
Fourier's law
The law of Heat Conduction, also known as FourierJoseph Fourier
Jean Baptiste Joseph Fourier was a French mathematician and physicist best known for initiating the investigation of Fourier series and their applications to problems of heat transfer and vibrations. The Fourier transform and Fourier's Law are also named in his honour...
's law, states that the time rate of heat transfer
Heat transfer
Heat transfer is a discipline of thermal engineering that concerns the exchange of thermal energy from one physical system to another. Heat transfer is classified into various mechanisms, such as heat conduction, convection, thermal radiation, and phase-change transfer...
through a material is proportional
Proportionality (mathematics)
In mathematics, two variable quantities are proportional if one of them is always the product of the other and a constant quantity, called the coefficient of proportionality or proportionality constant. In other words, are proportional if the ratio \tfrac yx is constant. We also say that one...
to the negative gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
in the temperature and to the area, at right angles to that gradient, through which the heat is flowing. We can state this law in two equivalent forms: the integral form, in which we look at the amount of energy flowing into or out of a body as a whole, and the differential form, in which we look at the flow rates or fluxes
Heat flux
Heat flux or thermal flux is the rate of heat energy transfer through a given surface. The SI derived unit of heat rate is joule per second, or watt. Heat flux is the heat rate per unit area. In SI units, heat flux is measured in W/m2]. Heat rate is a scalar quantity, while heat flux is a vectorial...
of energy locally.
Newton's law of cooling is a discrete analog of Fourier's law, while Ohm's law
Ohm's law
Ohm's law states that the current through a conductor between two points is directly proportional to the potential difference across the two points...
is the electrical analogue of Fourier's law.
Differential form
The differential form of Fourier's Law of thermal conduction shows that the local heat fluxHeat flux
Heat flux or thermal flux is the rate of heat energy transfer through a given surface. The SI derived unit of heat rate is joule per second, or watt. Heat flux is the heat rate per unit area. In SI units, heat flux is measured in W/m2]. Heat rate is a scalar quantity, while heat flux is a vectorial...
density,
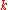, is equal to the product of thermal conductivity, , and the negative local temperature gradient, . The heat flux density is the amount of energy that flows through a unit area per unit time.
where (including the SI
Si
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
units)
-
is the local heat flux, WWattThe watt is a derived unit of power in the International System of Units , named after the Scottish engineer James Watt . The unit, defined as one joule per second, measures the rate of energy conversion.-Definition:...
·m−2 -
is the material's conductivityThermal conductivityIn physics, thermal conductivity, k, is the property of a material's ability to conduct heat. It appears primarily in Fourier's Law for heat conduction....
, WWattThe watt is a derived unit of power in the International System of Units , named after the Scottish engineer James Watt . The unit, defined as one joule per second, measures the rate of energy conversion.-Definition:...
·m−1·KKelvinThe kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...
−1, -
is the temperature gradient, KKelvinThe kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...
·m−1.
The thermal conductivity,
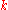, is often treated as a constant, though this is not always true. While the thermal conductivity of a material generally varies with temperature, the variation can be small over a significant range of temperatures for some common materials. In anisotropic materials, the thermal conductivity typically varies with orientation; in this case 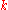is represented by a second-order tensorTensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
. In nonuniform materials,
varies with spatial location.For many simple applications, Fourier's law is used in its one-dimensional form. In the x-direction,
Integral form
By integrating the differential form over the material's total surface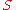, we arrive at the integral form of Fourier's law:
where (including the SI
Si
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
units)
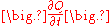is the amount of heat transferred per unit time (in W) and
is an oriented surface area element (in m2)
The above differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
, when integrated
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
for a homogeneous material of 1-D geometry between two endpoints at constant temperature, gives the heat flow rate as:
where
- A is the cross-sectional surface area,
-
is the temperature difference between the ends, -
is the distance between the ends.
This law forms the basis for the derivation of the heat equation
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
.
Conductance
Writing
where U is the conductance, in W/(m2 K).
Fourier's law can also be stated as:
The reciprocal of conductance is resistance, R, given by:
and it is resistance which is additive when several conducting layers lie between the hot and cool regions, because A and Q are the same for all layers. In a multilayer partition, the total conductance is related to the conductance of its layers by:
So, when dealing with a multilayer partition, the following formula is usually used:
When heat is being conducted from one fluid to another through a barrier, it is sometimes important to consider the conductance of the thin film
Thin film
A thin film is a layer of material ranging from fractions of a nanometer to several micrometers in thickness. Electronic semiconductor devices and optical coatings are the main applications benefiting from thin film construction....
of fluid which remains stationary next to the barrier. This thin film of fluid is difficult to quantify, its characteristics depending upon complex conditions of turbulence
Turbulence
In fluid dynamics, turbulence or turbulent flow is a flow regime characterized by chaotic and stochastic property changes. This includes low momentum diffusion, high momentum convection, and rapid variation of pressure and velocity in space and time...
and viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
, but when dealing with thin high-conductance barriers it can sometimes be quite significant.
Intensive-property representation
The previous conductance equations, written in terms of extensive propertiesIntensive and extensive properties
In the physical sciences, an intensive property , is a physical property of a system that does not depend on the system size or the amount of material in the system: it is scale invariant.By contrast, an extensive property In the physical sciences, an intensive property (also called a bulk...
, can be reformulated in terms of intensive properties
Intensive and extensive properties
In the physical sciences, an intensive property , is a physical property of a system that does not depend on the system size or the amount of material in the system: it is scale invariant.By contrast, an extensive property In the physical sciences, an intensive property (also called a bulk...
.
Ideally, the formulae for conductance should produce a quantity with dimensions independent of distance, like Ohm's Law
Ohm's law
Ohm's law states that the current through a conductor between two points is directly proportional to the potential difference across the two points...
for electrical resistance:
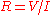, and conductance: .From the electrical formula:
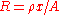, where ρ is resistivity, x = length, and A is cross-sectional area, we have 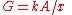, where G is conductance, k is conductivity, x = length, and A = cross-sectional area.For Heat,
where U is the conductance.
Fourier's law can also be stated as:
analogous to Ohm's law:
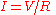or The reciprocal of conductance is resistance, R, given by:
analogous to Ohm's law:
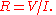
The rules for combining resistances and conductances (in series and in parallel) are the same for both heat flow and electric current.
Cylinders
Conduction through cylinders can be calculated when variables such as the internal radius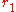, the external radius , and the length denoted as 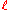.The temperature difference between the inner and outer wall can be expressed as
.The area of the heat flow:
When Fourier’s equation is applied:
Rearranged:
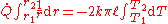
Therefore the rate of heat transfer is
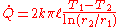
The thermal resistance is
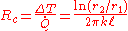
And
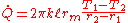, where 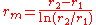and it is important to note that this is the log-mean radius.Spherical
internal radius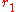, the external radius 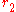of a spherical shell,The surface area
Surface area
Surface area is the measure of how much exposed area a solid object has, expressed in square units. Mathematical description of the surface area is considerably more involved than the definition of arc length of a curve. For polyhedra the surface area is the sum of the areas of its faces...
of a sphere is given by the following formula
and solve rest of the spherical part as we solved for cylindrical shell(see above topic).
and finally we get
Zeroth law of thermodynamics
One statement of the so-called zeroth law of thermodynamicsZeroth law of thermodynamics
The zeroth law of thermodynamics is a generalization principle of thermal equilibrium among bodies, or thermodynamic systems, in contact.The zeroth law states that if two systems are in thermal equilibrium with a third system, they are also in thermal equilibrium with each other.Systems are said to...
is directly focused on the idea of conduction of heat. Bailyn (1994) writes that "... the zeroth law may be stated:
-
- All diathermal walls are equivalent."
A diathermal wall is a connection of contiguity between two bodies that allows the passage of heat by conduction between them.
This statement of the 'zeroth law' belongs to an idealized theoretical discourse, and actual physical walls do not match its grandiloquent generality.
But with suitable restrictions, the statement has physical import. For example, the material of the wall must not suffer a phase transition, such as evaporation or fusion, at the temperature at which it has to conduct heat. But when only thermal equilibrium is being considered, and time is not urgent, so that the conductivity of the material does not matter too much, one suitable conductor of heat is as good as another. Conversely, another aspect of the zeroth law is that, subject again to suitable restrictions, a given diathermal wall is indifferent to the nature of the heat bath to which it is connected. For example the glass bulb of a thermometer will act as a diathermal wall whether exposed to a gas or to a liquid, provided they do not corrode it or melt it.
These indifferences are amongst the defining characteristics of heat transfer
Heat transfer
Heat transfer is a discipline of thermal engineering that concerns the exchange of thermal energy from one physical system to another. Heat transfer is classified into various mechanisms, such as heat conduction, convection, thermal radiation, and phase-change transfer...
. In a sense they are symmetries of heat transfer.
See also
- List of thermal conductivities
- Electrical conduction
- Convection diffusion equation
- U-value (insulation)
- Heat pipeHeat pipeA heat pipe or heat pin is a heat-transfer device that combines the principles of both thermal conductivity and phase transition to efficiently manage the transfer of heat between two solid interfaces....
- Fick's law of diffusionFick's law of diffusionFick's laws of diffusion describe diffusion and can be used to solve for the diffusion coefficient, D. They were derived by Adolf Fick in the year 1855.- Fick's first law :...
- Relativistic heat conductionRelativistic heat conductionThe theory of relativistic heat conduction claims to be the only model for heat conduction that is compatible with the theory of special relativity, the second law of thermodynamics, electrodynamics, and quantum mechanics, simultaneously...
- Thermomass theoryThermomass TheoryThermomass is defined as the equivalent mass of the thermal energy in heat transfer, which is determined by the Einstein’s mass-energy equivalence. The Thermomass theory, proposed by Prof. Zeng-Yuan Guo, regards heat owning the mass-energy duality, which exhibits energy-like features in conversion...
- Churchill-Bernstein EquationChurchill-Bernstein EquationIn convective heat transfer, the Churchill–Bernstein equation is used to estimate the surface averaged Nusselt number for a cylinder in cross flow at various velocities. The need for the equation arises from the inability to solve the Navier–Stokes equations in the turbulent flow regime, even for...
- Fourier numberFourier numberIn physics and engineering, the Fourier number or Fourier modulus, named after Joseph Fourier, is a dimensionless number that characterizes heat conduction. Conceptually, it is the ratio of the heat conduction rate to the rate of thermal energy storage. Together with the Biot number, it...
- Biot numberBiot numberThe Biot number is a dimensionless number used in non-steady-state heat transfer calculations. It is named after the French physicist Jean-Baptiste Biot , and gives a simple index of the ratio of the heat transfer resistances inside of and at the surface of a body...
External links
- Heat conduction - Thermal-FluidsPedia
- Newton's Law of Cooling by Jeff Bryant based on a program by Stephen WolframStephen WolframStephen Wolfram is a British scientist and the chief designer of the Mathematica software application and the Wolfram Alpha computational knowledge engine.- Biography :...
, Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
. - When Will My Turkey Be Done? is an example of applied heat conduction equations similar to Newton's Law of Cooling which predict the cooking time of turkeys and other roasts.