
Fuchsian model
Encyclopedia
In mathematics
, a Fuchsian model is a construction of a hyperbolic Riemann surface
R as a quotient of the upper half-plane H. By the uniformization theorem
, every Riemann surface is either elliptic
, parabolic or hyperbolic
. Every hyperbolic Riemann surface has a non-trivial fundamental group
 . The fundamental group can be shown to be isomorphic to some subgroup
. The fundamental group can be shown to be isomorphic to some subgroup
Γ of the group of real Möbius transformations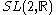 , this subgroup being a Fuchsian group
, this subgroup being a Fuchsian group
. The quotient space
H/Γ is then a Fuchsian model for the Riemann surface R. Many authors use the terms Fuchsian group and Fuchsian model interchangeably, letting the one stand for the other. The latter remark is true mostly of the creator of this page. Meanwhile, Matsuzaki reserves the term Fuchsian model for the Fuchsian group, never the surface itself.
that is either the Riemann sphere
, the complex plane
or the upper half-plane. Given a covering map
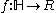 , where H is the upper half-plane.
, where H is the upper half-plane.
The Fuchsian model of R is the quotient space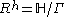 . R. Note that
. R. Note that 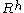 is a complete
is a complete
2D hyperbolic manifold.
of a closed Riemann surface is the same as its geometry
.
More precisely, let R be a closed
hyperbolic surface. Let G be the Fuchsian group of R and let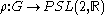 be a faithful representation of G, and let
be a faithful representation of G, and let 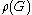 be discrete. Then define the set
be discrete. Then define the set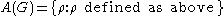
and add to this set a topology
of pointwise convergence, so that A(G) is an algebraic topology.
The Nielsen isomorphism theorem: For any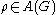 there exists a homeomorphism
there exists a homeomorphism
h of the upper half-plane H such that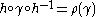 for all
for all 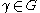 .
.
Most of the material here is copied, not very accurately, out of the book below (see page 12).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Fuchsian model is a construction of a hyperbolic Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
R as a quotient of the upper half-plane H. By the uniformization theorem
Uniformization theorem
In mathematics, the uniformization theorem says that any simply connected Riemann surface is conformally equivalent to one of the three domains: the open unit disk, the complex plane, or the Riemann sphere. In particular it admits a Riemannian metric of constant curvature...
, every Riemann surface is either elliptic
Elliptic geometry
Elliptic geometry is a non-Euclidean geometry, in which, given a line L and a point p outside L, there exists no line parallel to L passing through p. Elliptic geometry, like hyperbolic geometry, violates Euclid's parallel postulate, which can be interpreted as asserting that there is exactly one...
, parabolic or hyperbolic
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
. Every hyperbolic Riemann surface has a non-trivial fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
 . The fundamental group can be shown to be isomorphic to some subgroup
. The fundamental group can be shown to be isomorphic to some subgroupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
Γ of the group of real Möbius transformations
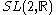 , this subgroup being a Fuchsian group
, this subgroup being a Fuchsian groupFuchsian group
In mathematics, a Fuchsian group is a discrete subgroup of PSL. The group PSL can be regarded as a group of isometries of the hyperbolic plane, or conformal transformations of the unit disc, or conformal transformations of the upper half plane, so a Fuchsian group can be regarded as a group acting...
. The quotient space
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
H/Γ is then a Fuchsian model for the Riemann surface R. Many authors use the terms Fuchsian group and Fuchsian model interchangeably, letting the one stand for the other. The latter remark is true mostly of the creator of this page. Meanwhile, Matsuzaki reserves the term Fuchsian model for the Fuchsian group, never the surface itself.
A more precise definition
To be more precise, every Riemann surface has a universal covering mapCovering map
In mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...
that is either the Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
, the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
or the upper half-plane. Given a covering map
Covering map
In mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...
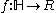 , where H is the upper half-plane.
, where H is the upper half-plane.The Fuchsian model of R is the quotient space
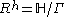 . R. Note that
. R. Note that 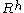 is a complete
is a completeComplete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
2D hyperbolic manifold.
Nielsen isomorphism theorem
The Nielsen isomorphism theorem basically states that the algebraic topologyAlgebraic topology (object)
In mathematics, the algebraic topology on the set of group representations from G to a topological group H is the topology of pointwise convergence, i.e...
of a closed Riemann surface is the same as its geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
.
More precisely, let R be a closed
Closed
Closed may refer to:Math* Closure * Closed manifold* Closed orbits* Closed set* Closed differential form* Closed map, a function that is closed.Other* Cloister, a closed walkway* Closed-circuit television...
hyperbolic surface. Let G be the Fuchsian group of R and let
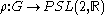 be a faithful representation of G, and let
be a faithful representation of G, and let 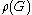 be discrete. Then define the set
be discrete. Then define the set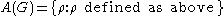
and add to this set a topology
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
of pointwise convergence, so that A(G) is an algebraic topology.
The Nielsen isomorphism theorem: For any
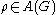 there exists a homeomorphism
there exists a homeomorphismHomeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
h of the upper half-plane H such that
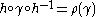 for all
for all 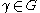 .
.Most of the material here is copied, not very accurately, out of the book below (see page 12).
See also
- the Kleinian model, an analogous construction for 3D manifolds
- Fundamental polygonFundamental polygonIn mathematics, each closed surface in the sense of geometric topology can be constructed from an even-sided oriented polygon, called a fundamental polygon, by pairwise identification of its edges....

