
De Rham curve
Encyclopedia
In mathematics
, a de Rham curve is a certain type of fractal
curve
named in honor of Georges de Rham
.
The Cantor function
, Césaro curve, Minkowski's question mark function
, the Lévy C curve
, the blancmange curve
and the Koch curve
are all special cases of the general de Rham curve.
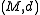 (generally
(generally 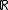 2 with the usual euclidean distance), and a pair of contracting map
2 with the usual euclidean distance), and a pair of contracting map
s on M:
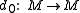
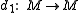
By the Banach fixed point theorem
, these have fixed points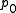 and
and 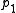 respectively. Let x be a real number
respectively. Let x be a real number
in the interval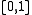 , having binary expansion
, having binary expansion
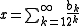
where each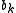 is 0 or 1. Consider the map
is 0 or 1. Consider the map
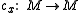
defined by
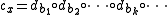
where denotes function composition
denotes function composition
. It can be shown that each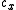 will map the common basin of attraction of
will map the common basin of attraction of  and
and 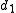 to a single point
to a single point 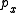 in
in 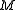 . The collection of points
. The collection of points 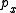 , parameterized by a single real parameter x, is known as the de Rham curve.
, parameterized by a single real parameter x, is known as the de Rham curve.
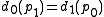
then it may be shown that the resulting curve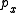 is a continuous function of x. When the curve is continuous, it is not in general differentiable.
is a continuous function of x. When the curve is continuous, it is not in general differentiable.
In the remaining of this page, we will assume the curves are continuous.
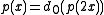 for
for 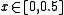 and
and  for
for 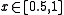 .
.
The self-symmetries of all of the de Rham curves are given by the monoid
that describes the symmetries of the infinite binary tree or Cantor set
. This so-called period-doubling monoid is a subset of the modular group
.
The image
of the curve, i.e. the set of points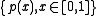 , can be obtained by an Iterated function system
, can be obtained by an Iterated function system
using the set of contraction mappings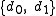 . But the result of an iterated function system with two contraction mappings is a de Rham curve if and only if the contraction mappings satisfy the continuity condition.
. But the result of an iterated function system with two contraction mappings is a de Rham curve if and only if the contraction mappings satisfy the continuity condition.
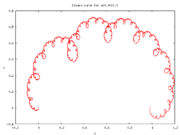
 Césaro curves (or Césaro-Faber curves) are De Rham curves generated by affine transformation
Césaro curves (or Césaro-Faber curves) are De Rham curves generated by affine transformation
s conserving orientation
, with fixed points and
and 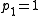 .
.
Because of these constraints, Césaro curves are uniquely determined by a complex number
 such that
such that 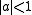 and
and 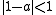 .
.
The contraction mappings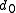 and
and 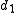 are then defined as complex functions in the complex plane
are then defined as complex functions in the complex plane
by:


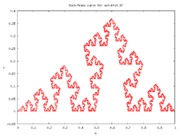
For the value of , the resulting curve is the Lévy C curve
, the resulting curve is the Lévy C curve
.
 In a similar way, we can define the Koch–Peano family of curves as the set of De Rham curves generated by affine transformations reversing orientation, with fixed points
In a similar way, we can define the Koch–Peano family of curves as the set of De Rham curves generated by affine transformations reversing orientation, with fixed points 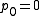 and
and  .
.
These mappings are expressed in the complex plane as a function of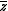 , the complex conjugate
, the complex conjugate
of :
:
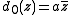
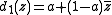
The name of the family comes from its two most famous members. The Koch curve
is obtained by setting:
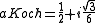
while the Peano curve corresponds to:
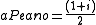



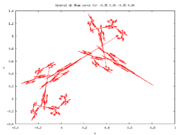 The Césaro-Faber and Peano-Koch curves are both special cases of the general case of a pair of affine linear transformations on the complex plane. By fixing one endpoint of the curve at 0 and the other at one, the general case is obtained by iterating on the two transforms
The Césaro-Faber and Peano-Koch curves are both special cases of the general case of a pair of affine linear transformations on the complex plane. By fixing one endpoint of the curve at 0 and the other at one, the general case is obtained by iterating on the two transforms
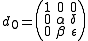
and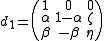
Being affine transforms, these transforms act on a point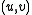 of the 2-D plane by acting on the vector
of the 2-D plane by acting on the vector
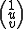
The midpoint of the curve can be seen to be located at ; the other four parameters may be varied to create a large variety of curves.
; the other four parameters may be varied to create a large variety of curves.
The blancmange curve
of parameter can be obtained by setting
can be obtained by setting  ,
,  and
and 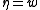 . That is:
. That is:
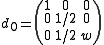
and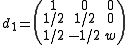
Since the blancmange curve of parameter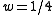 is the parabola of equation
is the parabola of equation 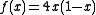 , this illustrate the fact that in some occasion, de Rham curves can be smooth.
, this illustrate the fact that in some occasion, de Rham curves can be smooth.
is generated by the pair of maps
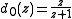
and
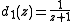
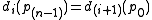 , for
, for 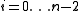 .
.
Such a generalization allows, for example, to produce the Sierpiński arrowhead curve
(whose image is the Sierpiński triangle
), by using the contraction mappings of an iterated function system that produces the Sierpiński triangle.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a de Rham curve is a certain type of fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
named in honor of Georges de Rham
Georges de Rham
Georges de Rham was a Swiss mathematician, known for his contributions to differential topology.He studied at the University of Lausanne and then in Paris for a doctorate, becoming a lecturer in Lausanne in 1931; where he held positions until retirement in 1971; he held positions in Geneva in...
.
The Cantor function
Cantor function
In mathematics, the Cantor function, named after Georg Cantor, is an example of a function that is continuous, but not absolutely continuous. It is also referred to as the Devil's staircase.-Definition:See figure...
, Césaro curve, Minkowski's question mark function
Minkowski's question mark function
In mathematics, the Minkowski question mark function, sometimes called the slippery devil's staircase and denoted by ?, is a function possessing various unusual fractal properties, defined by Hermann Minkowski in 1904...
, the Lévy C curve
Lévy C curve
In mathematics, the Lévy C curve is a self-similar fractal that was first described and whose differentiability properties were analysed by Ernesto Cesàro in 1906 and G...
, the blancmange curve
Blancmange curve
In mathematics, the blancmange curve is a fractal curve constructible by midpoint subdivision. It is also known as the Takagi curve, after Teiji Takagi who described it in 1903, or as the Takagi–Landsberg curve, a generalization of the curve. The name blancmange comes from its resemblance to a...
and the Koch curve
Koch snowflake
The Koch snowflake is a mathematical curve and one of the earliest fractal curves to have been described...
are all special cases of the general de Rham curve.
Construction
Consider some metric spaceMetric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
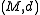 (generally
(generally  2 with the usual euclidean distance), and a pair of contracting map
2 with the usual euclidean distance), and a pair of contracting mapContraction mapping
In mathematics, a contraction mapping, or contraction, on a metric space is a function f from M to itself, with the property that there is some nonnegative real number k...
s on M:
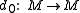
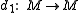
By the Banach fixed point theorem
Banach fixed point theorem
In mathematics, the Banach fixed-point theorem is an important tool in the theory of metric spaces; it guarantees the existence and uniqueness of fixed points of certain self-maps of metric spaces, and provides a constructive method to find those fixed points...
, these have fixed points
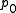 and
and 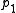 respectively. Let x be a real number
respectively. Let x be a real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
in the interval
 , having binary expansion
, having binary expansion
where each
 is 0 or 1. Consider the map
is 0 or 1. Consider the map
defined by
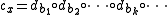
where
 denotes function composition
denotes function compositionFunction composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
. It can be shown that each
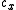 will map the common basin of attraction of
will map the common basin of attraction of  and
and 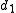 to a single point
to a single point 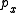 in
in 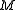 . The collection of points
. The collection of points 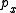 , parameterized by a single real parameter x, is known as the de Rham curve.
, parameterized by a single real parameter x, is known as the de Rham curve.Continuity Condition
When the fixed points are paired such that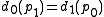
then it may be shown that the resulting curve
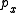 is a continuous function of x. When the curve is continuous, it is not in general differentiable.
is a continuous function of x. When the curve is continuous, it is not in general differentiable.In the remaining of this page, we will assume the curves are continuous.
Properties
De Rham curves are by construction self-similar, since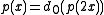 for
for 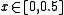 and
and  for
for 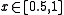 .
.The self-symmetries of all of the de Rham curves are given by the monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
that describes the symmetries of the infinite binary tree or Cantor set
Cantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
. This so-called period-doubling monoid is a subset of the modular group
Modular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
.
The image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of the curve, i.e. the set of points
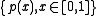 , can be obtained by an Iterated function system
, can be obtained by an Iterated function systemIterated function system
In mathematics, iterated function systems or IFSs are a method of constructing fractals; the resulting constructions are always self-similar....
using the set of contraction mappings
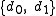 . But the result of an iterated function system with two contraction mappings is a de Rham curve if and only if the contraction mappings satisfy the continuity condition.
. But the result of an iterated function system with two contraction mappings is a de Rham curve if and only if the contraction mappings satisfy the continuity condition.Césaro curves


Affine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
s conserving orientation
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
, with fixed points
 and
and 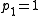 .
.Because of these constraints, Césaro curves are uniquely determined by a complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
 such that
such that 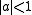 and
and 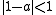 .
.The contraction mappings
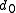 and
and 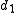 are then defined as complex functions in the complex plane
are then defined as complex functions in the complex planeComplex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
by:


For the value of
 , the resulting curve is the Lévy C curve
, the resulting curve is the Lévy C curveLévy C curve
In mathematics, the Lévy C curve is a self-similar fractal that was first described and whose differentiability properties were analysed by Ernesto Cesàro in 1906 and G...
.
Koch–Peano curves


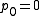 and
and  .
.These mappings are expressed in the complex plane as a function of
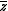 , the complex conjugate
, the complex conjugateComplex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
of
 :
: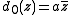
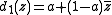
The name of the family comes from its two most famous members. The Koch curve
Koch snowflake
The Koch snowflake is a mathematical curve and one of the earliest fractal curves to have been described...
is obtained by setting:
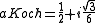
while the Peano curve corresponds to:
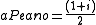
General affine maps




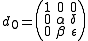
and
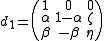
Being affine transforms, these transforms act on a point
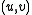 of the 2-D plane by acting on the vector
of the 2-D plane by acting on the vector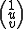
The midpoint of the curve can be seen to be located at
 ; the other four parameters may be varied to create a large variety of curves.
; the other four parameters may be varied to create a large variety of curves.The blancmange curve
Blancmange curve
In mathematics, the blancmange curve is a fractal curve constructible by midpoint subdivision. It is also known as the Takagi curve, after Teiji Takagi who described it in 1903, or as the Takagi–Landsberg curve, a generalization of the curve. The name blancmange comes from its resemblance to a...
of parameter
 can be obtained by setting
can be obtained by setting  ,
,  and
and 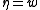 . That is:
. That is: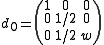
and
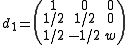
Since the blancmange curve of parameter
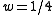 is the parabola of equation
is the parabola of equation 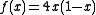 , this illustrate the fact that in some occasion, de Rham curves can be smooth.
, this illustrate the fact that in some occasion, de Rham curves can be smooth.Minkowski's question mark function
Minkowski's question mark functionMinkowski's question mark function
In mathematics, the Minkowski question mark function, sometimes called the slippery devil's staircase and denoted by ?, is a function possessing various unusual fractal properties, defined by Hermann Minkowski in 1904...
is generated by the pair of maps
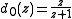
and
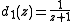
Generalizations
It is easy to generalize the definition by using more than two contraction mappings. If one uses n mappings, then the n-ary decomposition of x has to be used instead of the binary expansion of real numbers. The continuity condition has to be generalized in: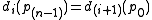 , for
, for 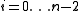 .
.Such a generalization allows, for example, to produce the Sierpiński arrowhead curve
Sierpinski arrowhead curve
The Sierpiński arrowhead curve is a fractal curve similar in appearance and identical in limit to the Sierpiński triangle.-Representation as Lindenmayer system:The Sierpiński arrowhead curve can be expressed by a rewrite system .-Literature:...
(whose image is the Sierpiński triangle
Sierpinski triangle
The Sierpinski triangle , also called the Sierpinski gasket or the Sierpinski Sieve, is a fractal and attractive fixed set named after the Polish mathematician Wacław Sierpiński who described it in 1915. However, similar patterns appear already in the 13th-century Cosmati mosaics in the cathedral...
), by using the contraction mappings of an iterated function system that produces the Sierpiński triangle.
See also
- Iterated function systemIterated function systemIn mathematics, iterated function systems or IFSs are a method of constructing fractals; the resulting constructions are always self-similar....
- Refinable function
- Modular groupModular groupIn mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
- Fuchsian groupFuchsian groupIn mathematics, a Fuchsian group is a discrete subgroup of PSL. The group PSL can be regarded as a group of isometries of the hyperbolic plane, or conformal transformations of the unit disc, or conformal transformations of the upper half plane, so a Fuchsian group can be regarded as a group acting...

