Fredholm theory
Encyclopedia
In mathematics
, Fredholm theory is a theory of integral equation
s. In the narrowest sense, Fredholm theory concerns itself with the solution of the Fredholm integral equation
. In a broader sense, the abstract structure of Fredholm's theory is given in terms of the spectral theory
of Fredholm operator
s and Fredholm kernel
s on Hilbert space
. The theory is named in honour of Erik Ivar Fredholm
.
and functional analysis
. The outline presented here is broad, whereas the difficulty of formalizing this sketch is, of course, in the details.
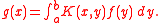
This equation arises naturally in many problems in physics
and mathematics, as the inverse of a differential equation
. That is, one is asked to solve the differential equation
where the function f is given and g is unknown. Here, L stands for a linear differential operator
. For example, one might take L to be an elliptic operator
, such as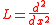
in which case the equation to be solved becomes the Poisson equation. A general method of solving such equations is by means of Green's function
s, namely, rather than a direct attack, one instead attempts to solve the equation
where
is the Dirac delta function
. The desired solution to the differential equation is then written as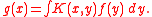
This integral is written in the form of a Fredholm integral equation
. The function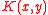
is variously known as a Green's function, or the kernel of an integral. It is sometimes called the nucleus of the integral, whence the term nuclear operator
arises.
In the general theory, x and y may be points on any manifold
; the real number line or m-dimensional Euclidean space
in the simplest cases. The general theory also often requires that the functions belong to some given function space
: often, the space of square-integrable function
s is studied, and Sobolev space
s appear often.
The actual function space used is often determined by the solutions of the eigenvalue problem of the differential operator; that is, by the solutions to
where the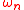
are the eigenvalues, and the 
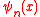are the eigenvectors. The set of eigenvectors span a Banach space
, and, when there is a natural inner product, then the eigenvectors span a Hilbert space
, at which point the Riesz representation theorem
is applied. Examples of such spaces are the orthogonal polynomials
that occur as the solutions to a class of second-order ordinary differential equation
s.
Given a Hilbert space as above, the kernel may be written in the form
where
is the dual
to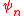
. In this form, the object 
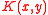is often called the Fredholm operator
or the Fredholm kernel
. That this is the same kernel as before follows from the complete
ness of the basis of the Hilbert space, namely, that one has
Since the
are generally increasing, the resulting eigenvalues of the operator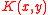 
are thus seen to be decreasing towards zero.
may be written formally as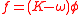
which has the formal solution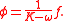
A solution of this form is referred to as the resolvent formalism
, where the resolvent is defined as the operator
Given the collection of eigenvectors and eigenvalues of K, the resolvent may be given a concrete form as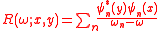
with the solution being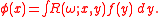
A necessary and sufficient condition for such a solution to exist is one of Fredholm's theorem
s. The resolvent is commonly expanded in powers of
, in which case it is known as the Liouville-Neumann series
. In this case, the integral equation is written as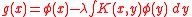
and the resolvent is written in the alternate form as
is commonly defined as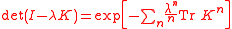
where
and
and so on. The corresponding zeta function is
The zeta function can be thought of as the determinant of the resolvent.
The zeta function plays an important role in studying dynamical systems. Note that this is the same general type of zeta function as the Riemann zeta function; however, in this case, the corresponding kernel is not known. The existence of such a kernel is known as the Hilbert–Pólya conjecture.
s, one of which is the Fredholm alternative
.
One of the important results from the general theory are that the kernel is a compact operator
when the space of functions are equicontinuous.
A related celebrated result is the Atiyah–Singer index theorem
, pertaining to index (dim ker – dim coker) of elliptic operators on compact manifolds.
. David Hilbert
developed the abstraction of Hilbert space
in association with research on integral equations prompted by Fredholm's (amongst other things).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Fredholm theory is a theory of integral equation
Integral equation
In mathematics, an integral equation is an equation in which an unknown function appears under an integral sign. There is a close connection between differential and integral equations, and some problems may be formulated either way...
s. In the narrowest sense, Fredholm theory concerns itself with the solution of the Fredholm integral equation
Fredholm integral equation
In mathematics, the Fredholm integral equation is an integral equation whose solution gives rise to Fredholm theory, the study of Fredholm kernels and Fredholm operators. The integral equation was studied by Ivar Fredholm.-Equation of the first kind :...
. In a broader sense, the abstract structure of Fredholm's theory is given in terms of the spectral theory
Spectral theory
In mathematics, spectral theory is an inclusive term for theories extending the eigenvector and eigenvalue theory of a single square matrix to a much broader theory of the structure of operators in a variety of mathematical spaces. It is a result of studies of linear algebra and the solutions of...
of Fredholm operator
Fredholm operator
In mathematics, a Fredholm operator is an operator that arises in the Fredholm theory of integral equations. It is named in honour of Erik Ivar Fredholm....
s and Fredholm kernel
Fredholm kernel
In mathematics, a Fredholm kernel is a certain type of a kernel on a Banach space, associated with nuclear operators on the Banach space. They are an abstraction of the idea of the Fredholm integral equation and the Fredholm operator, and are one of the objects of study in Fredholm theory....
s on Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
. The theory is named in honour of Erik Ivar Fredholm
Erik Ivar Fredholm
Erik Ivar Fredholm was a Swedish mathematician who established the modern theory of integral equations. His 1903 paper in Acta Mathematica is considered to be one of the major landmarks in the establishment of operator theory.The lunar crater Fredholm is named after him.-List of publications:* E.I...
.
Overview
The following sections provide a casual sketch of the place of Fredholm theory in the broader context of operator theoryOperator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
and functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
. The outline presented here is broad, whereas the difficulty of formalizing this sketch is, of course, in the details.
Homogeneous equations
Much of Fredholm theory concerns itself with finding solutions for the integral equationIntegral equation
In mathematics, an integral equation is an equation in which an unknown function appears under an integral sign. There is a close connection between differential and integral equations, and some problems may be formulated either way...
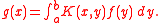
This equation arises naturally in many problems in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and mathematics, as the inverse of a differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
. That is, one is asked to solve the differential equation
where the function f is given and g is unknown. Here, L stands for a linear differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
. For example, one might take L to be an elliptic operator
Elliptic operator
In the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
, such as
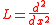
in which case the equation to be solved becomes the Poisson equation. A general method of solving such equations is by means of Green's function
Green's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
s, namely, rather than a direct attack, one instead attempts to solve the equation
where
is the Dirac delta functionDirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
. The desired solution to the differential equation is then written as
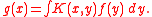
This integral is written in the form of a Fredholm integral equation
Fredholm integral equation
In mathematics, the Fredholm integral equation is an integral equation whose solution gives rise to Fredholm theory, the study of Fredholm kernels and Fredholm operators. The integral equation was studied by Ivar Fredholm.-Equation of the first kind :...
. The function
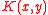is variously known as a Green's function, or the kernel of an integral. It is sometimes called the nucleus of the integral, whence the term nuclear operatorNuclear operator
In mathematics, a nuclear operator is roughly a compact operator for which a trace may be defined, such that the trace is finite and independent of the choice of basis .Nuclear operators are essentially the same as trace class operators, though most authors reserve the term "trace...
arises.
In the general theory, x and y may be points on any manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
; the real number line or m-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
in the simplest cases. The general theory also often requires that the functions belong to some given function space
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
: often, the space of square-integrable function
Square-integrable function
In mathematics, a quadratically integrable function, also called a square-integrable function, is a real- or complex-valued measurable function for which the integral of the square of the absolute value is finite...
s is studied, and Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
s appear often.
The actual function space used is often determined by the solutions of the eigenvalue problem of the differential operator; that is, by the solutions to
where the
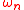are the eigenvalues, and the 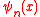are the eigenvectors. The set of eigenvectors span a Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
, and, when there is a natural inner product, then the eigenvectors span a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
, at which point the Riesz representation theorem
Riesz representation theorem
There are several well-known theorems in functional analysis known as the Riesz representation theorem. They are named in honour of Frigyes Riesz.- The Hilbert space representation theorem :...
is applied. Examples of such spaces are the orthogonal polynomials
Orthogonal polynomials
In mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
that occur as the solutions to a class of second-order ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s.
Given a Hilbert space as above, the kernel may be written in the form
where
is the dualDual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
to
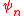. In this form, the object 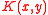is often called the Fredholm operatorFredholm operator
In mathematics, a Fredholm operator is an operator that arises in the Fredholm theory of integral equations. It is named in honour of Erik Ivar Fredholm....
or the Fredholm kernel
Fredholm kernel
In mathematics, a Fredholm kernel is a certain type of a kernel on a Banach space, associated with nuclear operators on the Banach space. They are an abstraction of the idea of the Fredholm integral equation and the Fredholm operator, and are one of the objects of study in Fredholm theory....
. That this is the same kernel as before follows from the complete
Complete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
ness of the basis of the Hilbert space, namely, that one has
Since the
are generally increasing, the resulting eigenvalues of the operator 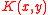are thus seen to be decreasing towards zero.Inhomogenous equations
The inhomogenous Fredholm integral equationmay be written formally as
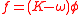
which has the formal solution
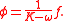
A solution of this form is referred to as the resolvent formalism
Resolvent formalism
In mathematics, the resolvent formalism is a technique for applying concepts from complex analysis to the study of the spectrum of operators on Hilbert spaces and more general spaces....
, where the resolvent is defined as the operator
Given the collection of eigenvectors and eigenvalues of K, the resolvent may be given a concrete form as
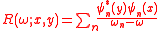
with the solution being
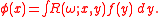
A necessary and sufficient condition for such a solution to exist is one of Fredholm's theorem
Fredholm's theorem
In mathematics, Fredholm's theorems are a set of celebrated results of Ivar Fredholm in the Fredholm theory of integral equations. There are several closely related theorems, which may be stated in terms of integral equations, in terms of linear algebra, or in terms of the Fredholm operator on...
s. The resolvent is commonly expanded in powers of
, in which case it is known as the Liouville-Neumann seriesLiouville-Neumann series
In mathematics, the Liouville–Neumann series is an infinite series that corresponds to the resolvent formalism technique of solving the Fredholm integral equations in Fredholm theory.-Definition:The Liouville–Neumann series is defined as...
. In this case, the integral equation is written as
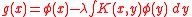
and the resolvent is written in the alternate form as
Fredholm determinant
The Fredholm determinantFredholm determinant
In mathematics, the Fredholm determinant is a complex-valued function which generalizes the determinant of a matrix. It is defined for bounded operators on a Hilbert space which differ from the identity operator by a trace-class operator...
is commonly defined as
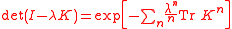
where
and
and so on. The corresponding zeta function is
The zeta function can be thought of as the determinant of the resolvent.
The zeta function plays an important role in studying dynamical systems. Note that this is the same general type of zeta function as the Riemann zeta function; however, in this case, the corresponding kernel is not known. The existence of such a kernel is known as the Hilbert–Pólya conjecture.
Main results
The classical results of the theory are Fredholm's theoremFredholm's theorem
In mathematics, Fredholm's theorems are a set of celebrated results of Ivar Fredholm in the Fredholm theory of integral equations. There are several closely related theorems, which may be stated in terms of integral equations, in terms of linear algebra, or in terms of the Fredholm operator on...
s, one of which is the Fredholm alternative
Fredholm alternative
In mathematics, the Fredholm alternative, named after Ivar Fredholm, is one of Fredholm's theorems and is a result in Fredholm theory. It may be expressed in several ways, as a theorem of linear algebra, a theorem of integral equations, or as a theorem on Fredholm operators...
.
One of the important results from the general theory are that the kernel is a compact operator
Compact operator
In functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
when the space of functions are equicontinuous.
A related celebrated result is the Atiyah–Singer index theorem
Atiyah–Singer index theorem
In differential geometry, the Atiyah–Singer index theorem, proved by , states that for an elliptic differential operator on a compact manifold, the analytical index is equal to the topological index...
, pertaining to index (dim ker – dim coker) of elliptic operators on compact manifolds.
History
Fredholm's 1903 paper in Acta Mathematica is considered to be one of the major landmarks in the establishment of operator theoryOperator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
. David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
developed the abstraction of Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
in association with research on integral equations prompted by Fredholm's (amongst other things).