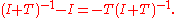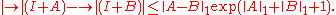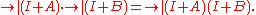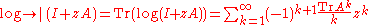Fredholm determinant
Encyclopedia
In mathematics
, the Fredholm determinant is a complex-valued function which generalizes the determinant
of a matrix
. It is defined for bounded operator
s on a Hilbert space
which differ from the identity operator by a trace-class operator. The function is named after the mathematician
Erik Ivar Fredholm
.
Fredholm determinants have had many applications in mathematical physics
, the most celebrated example being Gábor Szegő
's limit formula, proved in response to a question raised by Lars Onsager
and C. N. Yang on the spontaneous magnetization
of the Ising model
.
and G the set of bounded invertible operators
on H of the form I + T, where T is a trace-class operator. G is a group
because
It has a natural metric given by d(X, Y) = ||X - Y||1, where || · ||1 is the trace-class norm.
If H is a Hilbert space with inner product , then so too is the kth exterior power
, then so too is the kth exterior power
λk H with inner product
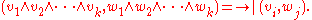
In particular
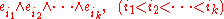
gives an orthonormal basis
of λk H if (ei) is an orthonormal basis of H.
If A is a bounded operator on H, then A functorially defines a bounded operator λk(A)
on λk H by
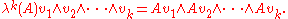
If A is trace-class, then λk(A) is also trace-class with
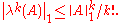
This shows that the definition of the Fredholm determinant given by

makes sense.
One can improve this inequality slightly to the following, as noted in Chapter 5 of Simon:
the limit
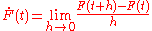
exists in trace-class norm.
If g(t) is a differentiable function with values in trace-class operators, then so too is exp g(t) and
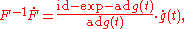
where
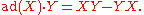
Israel Gohberg
and Mark Krein proved that if F is a differentiable function into G, then f = det F is a differentiable map into
C* with
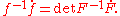
This result was used by Joel Pincus, William Helton and Roger Howe
to prove that if A and B are bounded operators with trace-class commutator
AB -BA, then
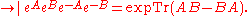
H2 (S1).
If f is a smooth function
on the circle, let m(f) denote the corresponding multiplication operator on H.
The commutator
is trace-class.
Let T(f) is the Toeplitz operator
on H2 (S1) defined by
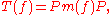
then the additive commutator

is trace-class if f and g are smooth.
Berger and Shaw proved that
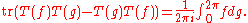
If f and g are smooth, then
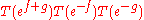
is in G.
Harold Widom
used the result of Pincus-Helton-Howe to prove that

where

He used this to give a new proof of Gábor Szegő
's celebrated limit formula:
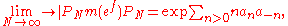
where PN is the projection onto the subspace of H spanned by 1, z, ..., zN and a0 = 0.
Szegő's limit formula was proved in 1951 in response to a question raised by the work Lars Onsager
and C. N. Yang on the calculation of the spontaneous magnetization
for the Ising model
. The formula of Widom, which leads quite quickly to Szegő's limit formula, is also equivalent to the duality between boson
s and fermion
s in conformal field theory
. A singular version of Szegő's limit formula for functions supported on an arc of the circle was proved by Widom; it has been applied to establish probabilistic results on the eigenvalue distribution of random unitary matrices
.
s and Banach space
s, this is a non-trivial exercise.
The Fredholm determinant may be defined as

where K is an integral operator. The trace of the operator is given by
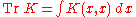
and

and in generall :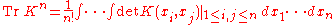
. The trace is well-defined for these kernels, since these are trace-class or nuclear operator
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Fredholm determinant is a complex-valued function which generalizes the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. It is defined for bounded operator
Bounded operator
In functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
s on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
which differ from the identity operator by a trace-class operator. The function is named after the mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Erik Ivar Fredholm
Erik Ivar Fredholm
Erik Ivar Fredholm was a Swedish mathematician who established the modern theory of integral equations. His 1903 paper in Acta Mathematica is considered to be one of the major landmarks in the establishment of operator theory.The lunar crater Fredholm is named after him.-List of publications:* E.I...
.
Fredholm determinants have had many applications in mathematical physics
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
, the most celebrated example being Gábor Szegő
Gábor Szego
Gábor Szegő was a Hungarian mathematician. He was one of the foremost analysts of his generation and made fundamental contributions to the theory of Toeplitz matrices and orthogonal polynomials.-Life:...
's limit formula, proved in response to a question raised by Lars Onsager
Lars Onsager
Lars Onsager was a Norwegian-born American physical chemist and theoretical physicist, winner of the 1968 Nobel Prize in Chemistry.He held the Gibbs Professorship of Theoretical Chemistry at Yale University....
and C. N. Yang on the spontaneous magnetization
Spontaneous magnetization
Spontaneous magnetization is the term used to describe the appearance of an ordered spin state at zero applied magnetic field in a ferromagnetic or ferrimagnetic material below a critical point called the Curie temperature or .-Overview:...
of the Ising model
Ising model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
.
Definition
Let H be a Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
and G the set of bounded invertible operators
Bounded operator
In functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
on H of the form I + T, where T is a trace-class operator. G is a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
because
It has a natural metric given by d(X, Y) = ||X - Y||1, where || · ||1 is the trace-class norm.
If H is a Hilbert space with inner product
 , then so too is the kth exterior power
, then so too is the kth exterior powerExterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
λk H with inner product
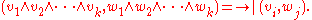
In particular
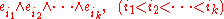
gives an orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
of λk H if (ei) is an orthonormal basis of H.
If A is a bounded operator on H, then A functorially defines a bounded operator λk(A)
on λk H by
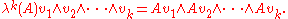
If A is trace-class, then λk(A) is also trace-class with
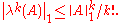
This shows that the definition of the Fredholm determinant given by

makes sense.
Properties
- If A is a trace-class operator.
- defines an entire functionEntire functionIn complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
such that
- The function det(I + A) is continuous on trace-class operators, with
One can improve this inequality slightly to the following, as noted in Chapter 5 of Simon:
- If A and B are trace-class then
- The function det defines a homomorphismHomomorphismIn abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
of G into the multiplicative group C* of non-zero complex numbers.
- If T is in G and X is invertible,
- If A is trace-class, then
Fredholm determinants of commutators
A function F(t) from (a, b) into G is said to be differentiable if F(t) -I is differentiable as a map into the trace-class operators, i.e. ifthe limit
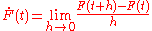
exists in trace-class norm.
If g(t) is a differentiable function with values in trace-class operators, then so too is exp g(t) and
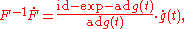
where
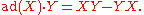
Israel Gohberg
Israel Gohberg
Israel Gohberg was a Bessarabian-born Soviet and Israeli mathematician, most known for his work in operator theory and functional analysis, in particular linear operators and integral equations...
and Mark Krein proved that if F is a differentiable function into G, then f = det F is a differentiable map into
C* with
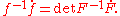
This result was used by Joel Pincus, William Helton and Roger Howe
Roger Evans Howe
Roger Evans Howe is the William R. Kenan Jr. Professor of Mathematics at Yale University. He is well known for his contributions to representation theory, and in particular for the notion of a reductive dual pair, sometimes known as a Howe pair, and the Howe correspondence.He attended Ithaca High...
to prove that if A and B are bounded operators with trace-class commutator
AB -BA, then
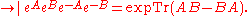
Szegő limit formula
Let H = L2 (S1) and let P be the orthogonal projection onto the Hardy spaceHardy space
In complex analysis, the Hardy spaces Hp are certain spaces of holomorphic functions on the unit disk or upper half plane. They were introduced by Frigyes Riesz , who named them after G. H. Hardy, because of the paper...
H2 (S1).
If f is a smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
on the circle, let m(f) denote the corresponding multiplication operator on H.
The commutator
- Pm(f) - m(f)P
is trace-class.
Let T(f) is the Toeplitz operator
Toeplitz operator
In operator theory, a Toeplitz operator is the compression of a multiplication operator on the circle to the Hardy space.- Details :Let S1 be the circle, with the standard Lebesgue measure, and L2 be the Hilbert space of square-integrable functions. A bounded measurable function g on S1 defines a...
on H2 (S1) defined by
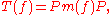
then the additive commutator

is trace-class if f and g are smooth.
Berger and Shaw proved that
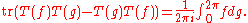
If f and g are smooth, then
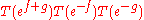
is in G.
Harold Widom
Harold Widom
Harold Widom is an American mathematician well known for his contributions to operator theory and random matrices. He was appointed to the Department of Mathematics at the University of California, Santa Cruz in 1968 and became professor emeritus in 1994. ...
used the result of Pincus-Helton-Howe to prove that

where

He used this to give a new proof of Gábor Szegő
Gábor Szego
Gábor Szegő was a Hungarian mathematician. He was one of the foremost analysts of his generation and made fundamental contributions to the theory of Toeplitz matrices and orthogonal polynomials.-Life:...
's celebrated limit formula:
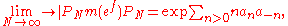
where PN is the projection onto the subspace of H spanned by 1, z, ..., zN and a0 = 0.
Szegő's limit formula was proved in 1951 in response to a question raised by the work Lars Onsager
Lars Onsager
Lars Onsager was a Norwegian-born American physical chemist and theoretical physicist, winner of the 1968 Nobel Prize in Chemistry.He held the Gibbs Professorship of Theoretical Chemistry at Yale University....
and C. N. Yang on the calculation of the spontaneous magnetization
Spontaneous magnetization
Spontaneous magnetization is the term used to describe the appearance of an ordered spin state at zero applied magnetic field in a ferromagnetic or ferrimagnetic material below a critical point called the Curie temperature or .-Overview:...
for the Ising model
Ising model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
. The formula of Widom, which leads quite quickly to Szegő's limit formula, is also equivalent to the duality between boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
s and fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s in conformal field theory
Conformal field theory
A conformal field theory is a quantum field theory that is invariant under conformal transformations...
. A singular version of Szegő's limit formula for functions supported on an arc of the circle was proved by Widom; it has been applied to establish probabilistic results on the eigenvalue distribution of random unitary matrices
Random matrix
In probability theory and mathematical physics, a random matrix is a matrix-valued random variable. Many important properties of physical systems can be represented mathematically as matrix problems...
.
Informal presentation
The section below provides an informal definition for the Fredholm determinant. A proper definition requires a presentation showing that each of the manipulations are well-defined, convergent, and so on, for the given situation for which the Fredholm determinant is contemplated. Since the kernel K may be defined on a large variety of Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s and Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s, this is a non-trivial exercise.
The Fredholm determinant may be defined as

where K is an integral operator. The trace of the operator is given by
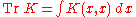
and

and in generall :
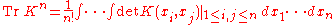
. The trace is well-defined for these kernels, since these are trace-class or nuclear operator
Nuclear operator
In mathematics, a nuclear operator is roughly a compact operator for which a trace may be defined, such that the trace is finite and independent of the choice of basis .Nuclear operators are essentially the same as trace class operators, though most authors reserve the term "trace...
s.