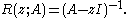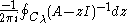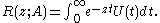Resolvent formalism
Encyclopedia
In mathematics
, the resolvent formalism is a technique for applying concepts from complex analysis
to the study of the spectrum
of operators on Hilbert space
s and more general spaces.
The resolvent captures the spectral properties of an operator in the analytic structure of the resolvent. Given an operator A, the resolvent may be defined as
Among other uses, the resolvent may be used to solve the inhomogeneous Fredholm integral equation
s; a commonly used approach is a series solution, the Liouville-Neumann series
.
The resolvent of A can be used to directly obtain information about the spectral decomposition
of A. For example, suppose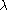
is an isolated eigenvalue in the
spectrum
of A. That is, suppose there exists a simple closed curve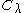
in the complex plane
that separates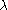
from the rest of the spectrum of A.
Then the residue
defines a projection operator onto the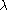
eigenspace of A.
The Hille-Yosida theorem relates the resolvent to an integral over the one-parameter group
of transformations generated by A. Thus, for example, if A is Hermitian, then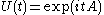
is a one-parameter group of unitary operators. The resolvent can be expressed as the integral
. The name resolvent was given by David Hilbert
.
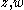in 
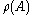, the resolvent set
of an operator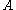
, we have that the resolvent identity (also called Hilbert's identity) holds: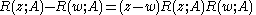
(Note that Dunford and Schwartz define the resolvent as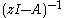
so that the formula above is slightly different from theirs.)
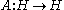on a Hilbert space
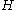, if there exists 
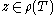such that 
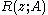is a compact operator
, we say that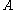
has compact resolvent. The spectrum 
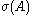of such 
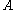is a discrete subset of 
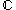. If furthermore 
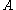is self-adjoint
, then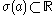
and there exists an orthonormal basis 
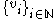of eigenvectors of 
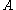with eigenvalues 
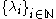respectively. Also, 
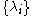has no finite accumulation point.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the resolvent formalism is a technique for applying concepts from complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
to the study of the spectrum
Spectrum (functional analysis)
In functional analysis, the concept of the spectrum of a bounded operator is a generalisation of the concept of eigenvalues for matrices. Specifically, a complex number λ is said to be in the spectrum of a bounded linear operator T if λI − T is not invertible, where I is the...
of operators on Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s and more general spaces.
The resolvent captures the spectral properties of an operator in the analytic structure of the resolvent. Given an operator A, the resolvent may be defined as
Among other uses, the resolvent may be used to solve the inhomogeneous Fredholm integral equation
Fredholm integral equation
In mathematics, the Fredholm integral equation is an integral equation whose solution gives rise to Fredholm theory, the study of Fredholm kernels and Fredholm operators. The integral equation was studied by Ivar Fredholm.-Equation of the first kind :...
s; a commonly used approach is a series solution, the Liouville-Neumann series
Liouville-Neumann series
In mathematics, the Liouville–Neumann series is an infinite series that corresponds to the resolvent formalism technique of solving the Fredholm integral equations in Fredholm theory.-Definition:The Liouville–Neumann series is defined as...
.
The resolvent of A can be used to directly obtain information about the spectral decomposition
of A. For example, suppose
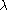is an isolated eigenvalue in thespectrum
Spectrum
A spectrum is a condition that is not limited to a specific set of values but can vary infinitely within a continuum. The word saw its first scientific use within the field of optics to describe the rainbow of colors in visible light when separated using a prism; it has since been applied by...
of A. That is, suppose there exists a simple closed curve
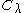
in the complex plane
that separates
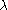from the rest of the spectrum of A.Then the residue
Residue (complex analysis)
In mathematics, more specifically complex analysis, the residue is a complex number proportional to the contour integral of a meromorphic function along a path enclosing one of its singularities...
defines a projection operator onto the
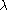eigenspace of A.The Hille-Yosida theorem relates the resolvent to an integral over the one-parameter group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of transformations generated by A. Thus, for example, if A is Hermitian, then
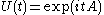is a one-parameter group of unitary operators. The resolvent can be expressed as the integral
History
The first major use of the resolvent operator was by Ivar Fredholm, in a landmark 1903 paper in Acta Mathematica that helped establish modern operator theoryOperator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
. The name resolvent was given by David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
.
Resolvent identity
For all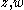 in 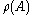, the resolvent setResolvent set
In linear algebra and operator theory, the resolvent set of a linear operator is a set of complex numbers for which the operator is in some sense "well-behaved". The resolvent set plays an important role in the resolvent formalism.-Definitions:...
of an operator
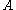, we have that the resolvent identity (also called Hilbert's identity) holds: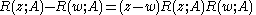(Note that Dunford and Schwartz define the resolvent as
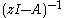so that the formula above is slightly different from theirs.)Compact resolvent
When studying an unbounded operatorUnbounded operator
In mathematics, more specifically functional analysis and operator theory, the notion of unbounded operator provides an abstract framework for dealing with differential operators, unbounded observables in quantum mechanics, and other cases....
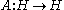on a Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
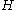, if there exists 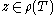such that 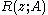is a compact operatorCompact operator
In functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
, we say that
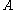has compact resolvent. The spectrum 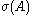of such 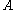is a discrete subset of 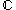. If furthermore 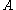is self-adjointSelf-adjoint
In mathematics, an element x of a star-algebra is self-adjoint if x^*=x.A collection C of elements of a star-algebra is self-adjoint if it is closed under the involution operation...
, then
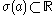and there exists an orthonormal basis 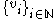of eigenvectors of 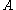with eigenvalues 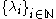respectively. Also, 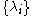has no finite accumulation point.See also
- Resolvent setResolvent setIn linear algebra and operator theory, the resolvent set of a linear operator is a set of complex numbers for which the operator is in some sense "well-behaved". The resolvent set plays an important role in the resolvent formalism.-Definitions:...
- Stone's theorem
- Holomorphic functional calculusHolomorphic functional calculusIn mathematics, holomorphic functional calculus is functional calculus with holomorphic functions. That is to say, given a holomorphic function ƒ of a complex argument z and an operator T, the aim is to construct an operatorf\,...
- Spectral theorySpectral theoryIn mathematics, spectral theory is an inclusive term for theories extending the eigenvector and eigenvalue theory of a single square matrix to a much broader theory of the structure of operators in a variety of mathematical spaces. It is a result of studies of linear algebra and the solutions of...
- Compact operatorCompact operatorIn functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
- Unbounded operatorUnbounded operatorIn mathematics, more specifically functional analysis and operator theory, the notion of unbounded operator provides an abstract framework for dealing with differential operators, unbounded observables in quantum mechanics, and other cases....