
Liouville-Neumann series
Encyclopedia
In mathematics
, the Liouville–Neumann series is an infinite series that corresponds to the resolvent formalism
technique of solving the Fredholm integral equation
s in Fredholm theory
.

which is a unique, continuous
solution of a Fredholm integral equation
of the second kind:

If the nth iterated kernel is defined as
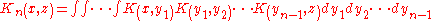
then
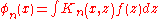
with

The resolvent or solving kernel is given by

The solution of the integral equation becomes
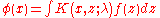
Similar methods may be used to solve the Volterra equations.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Liouville–Neumann series is an infinite series that corresponds to the resolvent formalism
Resolvent formalism
In mathematics, the resolvent formalism is a technique for applying concepts from complex analysis to the study of the spectrum of operators on Hilbert spaces and more general spaces....
technique of solving the Fredholm integral equation
Fredholm integral equation
In mathematics, the Fredholm integral equation is an integral equation whose solution gives rise to Fredholm theory, the study of Fredholm kernels and Fredholm operators. The integral equation was studied by Ivar Fredholm.-Equation of the first kind :...
s in Fredholm theory
Fredholm theory
In mathematics, Fredholm theory is a theory of integral equations. In the narrowest sense, Fredholm theory concerns itself with the solution of the Fredholm integral equation. In a broader sense, the abstract structure of Fredholm's theory is given in terms of the spectral theory of Fredholm...
.
Definition
The Liouville–Neumann series is defined as
which is a unique, continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
solution of a Fredholm integral equation
Fredholm integral equation
In mathematics, the Fredholm integral equation is an integral equation whose solution gives rise to Fredholm theory, the study of Fredholm kernels and Fredholm operators. The integral equation was studied by Ivar Fredholm.-Equation of the first kind :...
of the second kind:

If the nth iterated kernel is defined as
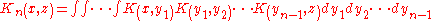
then
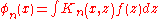
with

The resolvent or solving kernel is given by

The solution of the integral equation becomes
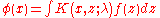
Similar methods may be used to solve the Volterra equations.

