
Field of sets
Encyclopedia
In mathematics
a field of sets is a pair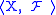 where
where  is a set and
is a set and 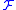 is an algebra over
is an algebra over  i.e., a non-empty subset of the power set of
i.e., a non-empty subset of the power set of  closed under the intersection
closed under the intersection
and union
of pairs of sets and under complements
of individual sets. In other words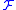 forms a subalgebra
forms a subalgebra
of the power set Boolean algebra of . (Many authors refer to
. (Many authors refer to 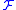 itself as a field of sets. The word "field" in "field of sets" is not used with the meaning of field from field theory
itself as a field of sets. The word "field" in "field of sets" is not used with the meaning of field from field theory
.) Elements of are called points and those of
are called points and those of 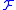 are called complexes.
are called complexes.
Fields of sets play an essential role in the representation theory
of Boolean algebras. Every Boolean algebra can be represented as a field of sets.
; each element of the Boolean algebra corresponds to the set of atoms below it (the join of which is the element). This power set representation can be constructed more generally for any complete
atomic
Boolean algebra.
In the case of Boolean algebras which are not complete and atomic we can still generalize the power set representation by considering fields of sets instead of whole power sets. To do this we first observe that the atoms of a finite Boolean algebra correspond to its ultrafilter
s and that an atom is below an element of a finite Boolean algebra if and only if that element is contained in the ultrafilter corresponding to the atom. This leads us to construct a representation of a Boolean algebra by taking its set of ultrafilters and forming complexes by associating with each element of the Boolean algebra the set of ultrafilters containing that element. This construction does indeed produce a representation of the Boolean algebra as a field of sets and is known as the Stone representation. It is the basis of Stone's representation theorem for Boolean algebras
and an example of a completion procedure in order theory
based on ideals or filter
s, similar to Dedekind cut
s.
Alternatively one can consider the set of homomorphism
s onto the two element Boolean algebra and form complexes by associating each element of the Boolean algebra with the set of such homomorphisms that map it to the top element. (The approach is equivalent as the ultrafilters of a Boolean algebra are precisely the pre-images of the top elements under these homomorphisms.) With this approach one sees that Stone representation can also be regarded as a generalization of the representation of finite Boolean algebras by truth table
s.
These definitions arise from considering the topology
generated by the complexes of a field of sets. Given a field of sets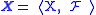 the complexes form a base
the complexes form a base
for a topology, we denote the corresponding topological space by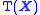 . Then
. Then
The Stone representation of a Boolean algebra is always separative and compact; the corresponding Boolean space is known as the Stone space of the Boolean algebra. The clopen sets of the Stone space are then precisely the complexes of the Stone representation. The area of mathematics known as Stone duality
is founded on the fact that the Stone representation of a Boolean algebra can be recovered purely from the corresponding Stone space whence a duality
exists between Boolean algebras and Boolean spaces.
and countable unions
, it is called a sigma algebra and the corresponding field of sets is called a measurable space. The complexes of a measurable space are called measurable sets.
A measure space is a triple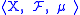 where
where  is a measurable space and
is a measurable space and  is a measure defined on it. If
is a measure defined on it. If  is in fact a probability measure
is in fact a probability measure
we speak of a probability space and call its underlying measurable space a sample space. The points of a sample space are called samples and represent potential outcomes while the measurable sets (complexes) are called events and represent properties of outcomes for which we wish to assign probabilities. (Many use the term sample space simply for the underlying set of a probability space, particularly in the case where every subset is an event.) Measure spaces and probability spaces play a foundational role in measure theory and probability theory
respectively.
The Loomis-Sikorski theorem provides a Stone-type duality between abstract sigma algebras and measurable spaces.
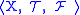 where
where 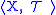 is a topological space
is a topological space
and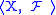 is a field of sets which is closed under the closure operator
is a field of sets which is closed under the closure operator
of or equivalently under the interior operator i.e. the closure and interior of every complex is also a complex. In other words
or equivalently under the interior operator i.e. the closure and interior of every complex is also a complex. In other words 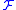 forms a subalgebra of the power set interior algebra
forms a subalgebra of the power set interior algebra
on .
.
Every interior algebra can be represented as a topological field of sets with its interior and closure operators corresponding to those of the topological space.
Given a topological space the clopen
sets trivially form a topological field of sets as each clopen set is its own interior and closure. The Stone representation of a Boolean algebra can be regarded as such a topological field of sets.
If a topological field of sets is both compact and algebraic then its topology is compact and its compact open sets are precisely the open complexes. Moreover the open complexes form a base for the topology.
Topological fields of sets that are separative, compact and algebraic are called Stone fields and provide a generalization of the Stone representation of Boolean algebras. Given an interior algebra we can form the Stone representation of its underlying Boolean algebra and then extend this to a topological field of sets by taking the topology generated by the complexes corresponding to the open elements of the interior algebra (which form a base for a topology). These complexes are then precisely the open complexes and the construction produces a Stone field representing the interior algebra - the Stone representation.
 where
where 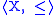 is a preordered set
is a preordered set
and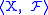 is a field of sets.
is a field of sets.
Like the topological fields of sets, preorder fields play an important role in the representation theory of interior algebras. Every interior algebra can be represented as a preorder field with its interior and closure operators corresponding to those of the Alexandrov topology
induced by the preorder. In other words
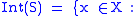 there exists a
there exists a 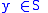 with
with 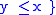 and
and there exists a
there exists a 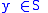 with
with  for all
for all 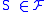
Preorder fields arise naturally in modal logic
where the points represent the possible worlds in the Kripke semantics
of a theory in the modal logic S4 (a formal mathematical abstraction of epistemic logic), the preorder represents the accessibility relation on these possible worlds in this semantics, and the complexes represent sets of possible worlds in which individual sentences in the theory hold, providing a representation of the Lindenbaum-Tarski algebra of the theory.
 which determines the preorder in the following manner:
which determines the preorder in the following manner:  if and only if for every complex
if and only if for every complex  ,
,  implies
implies 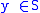 . The preorder fields obtained from S4 theories are always algebraic, the complexes determining the preorder being the sets of possible worlds in which the sentences of the theory closed under necessity hold.
. The preorder fields obtained from S4 theories are always algebraic, the complexes determining the preorder being the sets of possible worlds in which the sentences of the theory closed under necessity hold.
A separative compact algebraic preorder field is said to be canonical. Given an interior algebra, by replacing the topology of its Stone representation with the corresponding canonical preorder
(specialization preorder) we obtain a representation of the interior algebra as a canonical preorder field. By replacing the preorder by its corresponding Alexandrov topology we obtain an alternative representation of the interior algebra as a topological field of sets. (The topology of this "Alexandrov representation" is just the Alexandrov bi-coreflection of the topology of the Stone representation.)
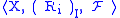 where
where 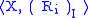 is a relational structure i.e. a set with an indexed family of relation
is a relational structure i.e. a set with an indexed family of relation
s defined on it, and is a field of sets. The complex algebra (or algebra of complexes) determined by a field of sets
is a field of sets. The complex algebra (or algebra of complexes) determined by a field of sets 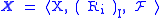 on a relational structure, is the Boolean algebra with operators
on a relational structure, is the Boolean algebra with operators
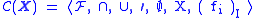
where for all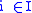 , if
, if 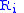 is a relation of arity
is a relation of arity  , then
, then 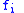 is an operator of arity
is an operator of arity  and for all
and for all 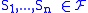
 there exist
there exist  such that
such that 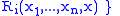
This construction can be generalized to fields of sets on arbitrary algebraic structure
s having both operators
and relations as operators can be viewed as a special case of relations. If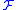 is the whole power set of
is the whole power set of  then
then  is called a full complex algebra or power algebra.
is called a full complex algebra or power algebra.
Every (normal) Boolean algebra with operators can be represented as a field of sets on a relational structure in the sense that it is isomorphic
to the complex algebra corresponding to the field.
(Historically the term complex was first used in the case where the algebraic structure was a group
and has its origins in 19th century group theory
where a subset of a group was called a complex.)
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
a field of sets is a pair
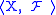 where
where  is a set and
is a set and 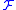 is an algebra over
is an algebra over  i.e., a non-empty subset of the power set of
i.e., a non-empty subset of the power set of  closed under the intersection
closed under the intersectionIntersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
and union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of pairs of sets and under complements
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of individual sets. In other words
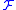 forms a subalgebra
forms a subalgebraSubalgebra
In mathematics, the word "algebra", when referring to a structure, often means a vector space or module equipped with an additional bilinear operation. Algebras in universal algebra are far more general: they are a common generalisation of all algebraic structures...
of the power set Boolean algebra of
 . (Many authors refer to
. (Many authors refer to 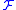 itself as a field of sets. The word "field" in "field of sets" is not used with the meaning of field from field theory
itself as a field of sets. The word "field" in "field of sets" is not used with the meaning of field from field theoryField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
.) Elements of
 are called points and those of
are called points and those of 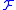 are called complexes.
are called complexes.Fields of sets play an essential role in the representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
of Boolean algebras. Every Boolean algebra can be represented as a field of sets.
Stone representation
Every finite Boolean algebra can be represented as a whole power set - the power set of its set of atomsAtomic (order theory)
In the mathematical field of order theory, given two elements a and b of a partially ordered set, one says that b covers a, and writes a a, if a ...
; each element of the Boolean algebra corresponds to the set of atoms below it (the join of which is the element). This power set representation can be constructed more generally for any complete
Complete Boolean algebra
In mathematics, a complete Boolean algebra is a Boolean algebra in which every subset has a supremum . Complete Boolean algebras are used to construct Boolean-valued models of set theory in the theory of forcing...
atomic
Atomic (order theory)
In the mathematical field of order theory, given two elements a and b of a partially ordered set, one says that b covers a, and writes a a, if a ...
Boolean algebra.
In the case of Boolean algebras which are not complete and atomic we can still generalize the power set representation by considering fields of sets instead of whole power sets. To do this we first observe that the atoms of a finite Boolean algebra correspond to its ultrafilter
Ultrafilter
In the mathematical field of set theory, an ultrafilter on a set X is a collection of subsets of X that is a filter, that cannot be enlarged . An ultrafilter may be considered as a finitely additive measure. Then every subset of X is either considered "almost everything" or "almost nothing"...
s and that an atom is below an element of a finite Boolean algebra if and only if that element is contained in the ultrafilter corresponding to the atom. This leads us to construct a representation of a Boolean algebra by taking its set of ultrafilters and forming complexes by associating with each element of the Boolean algebra the set of ultrafilters containing that element. This construction does indeed produce a representation of the Boolean algebra as a field of sets and is known as the Stone representation. It is the basis of Stone's representation theorem for Boolean algebras
Stone's representation theorem for Boolean algebras
In mathematics, Stone's representation theorem for Boolean algebras states that every Boolean algebra is isomorphic to a field of sets. The theorem is fundamental to the deeper understanding of Boolean algebra that emerged in the first half of the 20th century. The theorem was first proved by Stone...
and an example of a completion procedure in order theory
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
based on ideals or filter
Filter (mathematics)
In mathematics, a filter is a special subset of a partially ordered set. A frequently used special case is the situation that the ordered set under consideration is just the power set of some set, ordered by set inclusion. Filters appear in order and lattice theory, but can also be found in...
s, similar to Dedekind cut
Dedekind cut
In mathematics, a Dedekind cut, named after Richard Dedekind, is a partition of the rationals into two non-empty parts A and B, such that all elements of A are less than all elements of B, and A contains no greatest element....
s.
Alternatively one can consider the set of homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
s onto the two element Boolean algebra and form complexes by associating each element of the Boolean algebra with the set of such homomorphisms that map it to the top element. (The approach is equivalent as the ultrafilters of a Boolean algebra are precisely the pre-images of the top elements under these homomorphisms.) With this approach one sees that Stone representation can also be regarded as a generalization of the representation of finite Boolean algebras by truth table
Truth table
A truth table is a mathematical table used in logic—specifically in connection with Boolean algebra, boolean functions, and propositional calculus—to compute the functional values of logical expressions on each of their functional arguments, that is, on each combination of values taken by their...
s.
Separative and compact fields of sets: towards Stone duality
- A field of sets is called separative if and only if for every pair of distinct points there is a complex containing one and not the other.
- A field of sets is called compact if and only if for every proper filterFilter (mathematics)In mathematics, a filter is a special subset of a partially ordered set. A frequently used special case is the situation that the ordered set under consideration is just the power set of some set, ordered by set inclusion. Filters appear in order and lattice theory, but can also be found in...
over the intersection of all the complexes contained in the filter is non-empty.
the intersection of all the complexes contained in the filter is non-empty.
These definitions arise from considering the topology
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
generated by the complexes of a field of sets. Given a field of sets
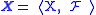 the complexes form a base
the complexes form a baseBase (topology)
In mathematics, a base B for a topological space X with topology T is a collection of open sets in T such that every open set in T can be written as a union of elements of B. We say that the base generates the topology T...
for a topology, we denote the corresponding topological space by
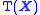 . Then
. Then-
 is always a zero-dimensional space.
is always a zero-dimensional space. -
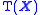 is a Hausdorff spaceHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
is a Hausdorff spaceHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
if and only if is separative.
is separative. -
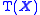 is a compact spaceCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
is a compact spaceCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
with compact open sets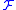 if and only if
if and only if  is compact.
is compact. -
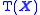 is a Boolean space with clopen sets
is a Boolean space with clopen sets 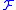 if and only if
if and only if  is both separative and compact.
is both separative and compact.
The Stone representation of a Boolean algebra is always separative and compact; the corresponding Boolean space is known as the Stone space of the Boolean algebra. The clopen sets of the Stone space are then precisely the complexes of the Stone representation. The area of mathematics known as Stone duality
Stone duality
In mathematics, there is an ample supply of categorical dualities between certain categories of topological spaces and categories of partially ordered sets. Today, these dualities are usually collected under the label Stone duality, since they form a natural generalization of Stone's representation...
is founded on the fact that the Stone representation of a Boolean algebra can be recovered purely from the corresponding Stone space whence a duality
Duality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
exists between Boolean algebras and Boolean spaces.
Sigma algebras and measure spaces
If an algebra over a set is closed under countable intersectionsIntersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
and countable unions
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
, it is called a sigma algebra and the corresponding field of sets is called a measurable space. The complexes of a measurable space are called measurable sets.
A measure space is a triple
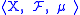 where
where  is a measurable space and
is a measurable space and  is a measure defined on it. If
is a measure defined on it. If  is in fact a probability measure
is in fact a probability measureProbability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
we speak of a probability space and call its underlying measurable space a sample space. The points of a sample space are called samples and represent potential outcomes while the measurable sets (complexes) are called events and represent properties of outcomes for which we wish to assign probabilities. (Many use the term sample space simply for the underlying set of a probability space, particularly in the case where every subset is an event.) Measure spaces and probability spaces play a foundational role in measure theory and probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
respectively.
The Loomis-Sikorski theorem provides a Stone-type duality between abstract sigma algebras and measurable spaces.
Topological fields of sets
A topological field of sets is a triple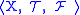 where
where 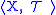 is a topological space
is a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
and
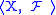 is a field of sets which is closed under the closure operator
is a field of sets which is closed under the closure operatorClosure operator
In mathematics, a closure operator on a set S is a function cl: P → P from the power set of S to itself which satisfies the following conditions for all sets X,Y ⊆ S....
of
 or equivalently under the interior operator i.e. the closure and interior of every complex is also a complex. In other words
or equivalently under the interior operator i.e. the closure and interior of every complex is also a complex. In other words 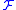 forms a subalgebra of the power set interior algebra
forms a subalgebra of the power set interior algebraInterior algebra
In abstract algebra, an interior algebra is a certain type of algebraic structure that encodes the idea of the topological interior of a set. Interior algebras are to topology and the modal logic S4 what Boolean algebras are to set theory and ordinary propositional logic...
on
 .
.Every interior algebra can be represented as a topological field of sets with its interior and closure operators corresponding to those of the topological space.
Given a topological space the clopen
Topology glossary
This is a glossary of some terms used in the branch of mathematics known as topology. Although there is no absolute distinction between different areas of topology, the focus here is on general topology...
sets trivially form a topological field of sets as each clopen set is its own interior and closure. The Stone representation of a Boolean algebra can be regarded as such a topological field of sets.
Algebraic fields of sets and Stone fields
A topological field of sets is called algebraic if and only if there is a base for its topology consisting of complexes.If a topological field of sets is both compact and algebraic then its topology is compact and its compact open sets are precisely the open complexes. Moreover the open complexes form a base for the topology.
Topological fields of sets that are separative, compact and algebraic are called Stone fields and provide a generalization of the Stone representation of Boolean algebras. Given an interior algebra we can form the Stone representation of its underlying Boolean algebra and then extend this to a topological field of sets by taking the topology generated by the complexes corresponding to the open elements of the interior algebra (which form a base for a topology). These complexes are then precisely the open complexes and the construction produces a Stone field representing the interior algebra - the Stone representation.
Preorder fields
A preorder field is a triple where
where 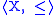 is a preordered set
is a preordered setPreorder
In mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders...
and
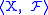 is a field of sets.
is a field of sets.Like the topological fields of sets, preorder fields play an important role in the representation theory of interior algebras. Every interior algebra can be represented as a preorder field with its interior and closure operators corresponding to those of the Alexandrov topology
Alexandrov topology
In topology, an Alexandrov space is a topological space in which the intersection of any family of open sets is open. It is an axiom of topology that the intersection of any finite family of open sets is open...
induced by the preorder. In other words
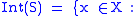 there exists a
there exists a 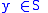 with
with 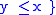 and
and there exists a
there exists a 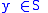 with
with  for all
for all 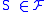
Preorder fields arise naturally in modal logic
Modal logic
Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
where the points represent the possible worlds in the Kripke semantics
Kripke semantics
Kripke semantics is a formal semantics for non-classical logic systems created in the late 1950s and early 1960s by Saul Kripke. It was first made for modal logics, and later adapted to intuitionistic logic and other non-classical systems...
of a theory in the modal logic S4 (a formal mathematical abstraction of epistemic logic), the preorder represents the accessibility relation on these possible worlds in this semantics, and the complexes represent sets of possible worlds in which individual sentences in the theory hold, providing a representation of the Lindenbaum-Tarski algebra of the theory.
Algebraic and canonical preorder fields
A preorder field is called algebraic if and only if it has a set of complexes which determines the preorder in the following manner:
which determines the preorder in the following manner:  if and only if for every complex
if and only if for every complex  ,
,  implies
implies 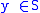 . The preorder fields obtained from S4 theories are always algebraic, the complexes determining the preorder being the sets of possible worlds in which the sentences of the theory closed under necessity hold.
. The preorder fields obtained from S4 theories are always algebraic, the complexes determining the preorder being the sets of possible worlds in which the sentences of the theory closed under necessity hold.A separative compact algebraic preorder field is said to be canonical. Given an interior algebra, by replacing the topology of its Stone representation with the corresponding canonical preorder
Specialization (pre)order
In the branch of mathematics known as topology, the specialization preorder is a natural preorder on the set of the points of a topological space. For most spaces that are considered in practice, namely for all those that satisfy the T0 separation axiom, this preorder is even a partial order...
(specialization preorder) we obtain a representation of the interior algebra as a canonical preorder field. By replacing the preorder by its corresponding Alexandrov topology we obtain an alternative representation of the interior algebra as a topological field of sets. (The topology of this "Alexandrov representation" is just the Alexandrov bi-coreflection of the topology of the Stone representation.)
Complex algebras and fields of sets on relational structures
The representation of interior algebras by preorder fields can be generalized to a representation theorem for arbitrary (normal) Boolean algebras with operators. For this we consider structures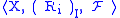 where
where 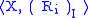 is a relational structure i.e. a set with an indexed family of relation
is a relational structure i.e. a set with an indexed family of relationRelation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
s defined on it, and
 is a field of sets. The complex algebra (or algebra of complexes) determined by a field of sets
is a field of sets. The complex algebra (or algebra of complexes) determined by a field of sets 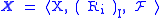 on a relational structure, is the Boolean algebra with operators
on a relational structure, is the Boolean algebra with operators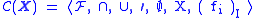
where for all
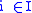 , if
, if 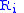 is a relation of arity
is a relation of arity  , then
, then 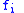 is an operator of arity
is an operator of arity  and for all
and for all 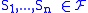
 there exist
there exist  such that
such that 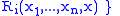
This construction can be generalized to fields of sets on arbitrary algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
s having both operators
Operation (mathematics)
The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
and relations as operators can be viewed as a special case of relations. If
 is the whole power set of
is the whole power set of  then
then  is called a full complex algebra or power algebra.
is called a full complex algebra or power algebra.Every (normal) Boolean algebra with operators can be represented as a field of sets on a relational structure in the sense that it is isomorphic
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
to the complex algebra corresponding to the field.
(Historically the term complex was first used in the case where the algebraic structure was a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
and has its origins in 19th century group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
where a subset of a group was called a complex.)
See also
- List of Boolean algebra topics
- Algebra of setsAlgebra of setsThe algebra of sets develops and describes the basic properties and laws of sets, the set-theoretic operations of union, intersection, and complementation and the relations of set equality and set inclusion...
- Sigma algebra
- Measure theory
- Probability theoryProbability theoryProbability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
- Interior algebraInterior algebraIn abstract algebra, an interior algebra is a certain type of algebraic structure that encodes the idea of the topological interior of a set. Interior algebras are to topology and the modal logic S4 what Boolean algebras are to set theory and ordinary propositional logic...
- Alexandrov topologyAlexandrov topologyIn topology, an Alexandrov space is a topological space in which the intersection of any family of open sets is open. It is an axiom of topology that the intersection of any finite family of open sets is open...
- Stone's representation theorem for Boolean algebrasStone's representation theorem for Boolean algebrasIn mathematics, Stone's representation theorem for Boolean algebras states that every Boolean algebra is isomorphic to a field of sets. The theorem is fundamental to the deeper understanding of Boolean algebra that emerged in the first half of the 20th century. The theorem was first proved by Stone...
- Stone dualityStone dualityIn mathematics, there is an ample supply of categorical dualities between certain categories of topological spaces and categories of partially ordered sets. Today, these dualities are usually collected under the label Stone duality, since they form a natural generalization of Stone's representation...
- Boolean ringBoolean ringIn mathematics, a Boolean ring R is a ring for which x2 = x for all x in R; that is, R consists only of idempotent elements....

