
Modal logic
Encyclopedia
Modal logic is a type of formal logic that extends classical propositional and predicate logic
to include operators expressing modality
. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is usually happy, in which case the term "usually" is functioning as a modal. The traditional alethic modalities
, or modalities of truth, include possibility
("Possibly, p", "It is possible that p"), necessity ("Necessarily, p", "It is necessary that p"), and impossibility ("It is impossible that p"). Other modalities that have been formalized in modal logic include temporal
modalities, or modalities or time (notably, "It was the case that p", "It has always been that p", "It will be that p", "It will always be that p"), deontic modalities (notably, "It is obligatory that p", and "It is permissible that p"), epistemic modalities, or modalities of knowledge ("It is known that p") and doxastic modalities, or modalities of belief ("It is believed that p").
A formal modal logic represents modalities using modal operator
s. For example, "It might rain today" and "It is possible that rain will fall today" both contain the notion of possibility. In a modal logic this is represented as an operator, Possibly, attached to the sentence "It will rain today".
The basic unary
(1-place) modal operators are usually written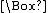 for Necessarily and
for Necessarily and  for Possibly. In a classical modal logic
for Possibly. In a classical modal logic
, each can be expressed by the other with negation
:
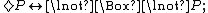
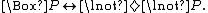
Thus it is possible that it will rain today if and only if it is not necessary that it will not rain today;
and it is necessary that it will rain today if and only if it is not possible that it will not rain today.
's logic is almost entirely concerned with the theory of the categorical syllogism, there are passages in his work, such as the famous sea-battle argument in De Interpretatione § 9, that are now seen as anticipations of modal logic and its connection with potentiality and time. Modal logic as a self-aware subject owes much to the writings of the Scholastics, in particular William of Ockham
and John Duns Scotus, who reasoned informally in a modal manner, mainly to analyze statements about essence
and accident
.
C. I. Lewis founded modern modal logic in his 1910 Harvard thesis and in a series of scholarly articles beginning in 1912. This work culminated in his 1932 book Symbolic Logic (with C. H. Langford), which introduced the five systems S1 through S5.
Ruth C. Barcan (later Ruth Barcan Marcus
) developed the first axiomatic systems of quantified modal logic — first and second order extensions of Lewis's "S2", "S4", and "S5".
The contemporary era in modal semantics began in 1959, when Saul Kripke
(then only a 19-year-old Harvard University
undergraduate) introduced the now-standard Kripke semantics
for modal logics. These are commonly referred to as "possible worlds" semantics. Kripke and A. N. Prior had previously corresponded at some length. Kripke semantics is basically simple, but proofs are eased using semantic-tableaus or analytic tableaux, as explained by E. W. Beth.
A. N. Prior created modern temporal logic
, closely related to modal logic, in 1957 by adding modal operators [F] and [P] meaning "henceforth" and "hitherto". Vaughan Pratt introduced dynamic logic
in 1976. In 1977, Amir Pnueli proposed using temporal logic to formalise the behaviour of continually operating concurrent programs. Flavors of temporal logic include propositional dynamic logic (PDL), propositional linear temporal logic (PLTL), linear temporal logic
(LTL), computational tree logic
(CTL), Hennessy–Milner logic
, and T.
The mathematical structure of modal logic, namely Boolean algebras augmented with unary operation
s (often called modal algebra
s), began to emerge with J. C. C. McKinsey's 1941 proof that S2 and S4 are decidable, and reached full flower in the work of Alfred Tarski
and his student Bjarni Jonsson
(Jonsson and Tarski 1951–52). This work revealed that S4 and S5 are models of interior algebra
, a proper extension of Boolean algebra originally designed to capture the properties of the interior and closure operator
s of topology
. Texts on modal logic typically do little more than mention its connections with the study of Boolean algebras and topology
. For a thorough survey of the history of formal modal logic and of the associated mathematics, see http://www.mcs.vuw.ac.nz/~rob/papers/modalhist.pdfRobert Goldblatt
(2006).]
First we define a frame, which consists of a non-empty set, G, whose members are generally called possible worlds, and a binary relation, R, that holds (or not) between the possible worlds of G. This binary relation is called the accessibility relation
. For example, w R v means that the world v is accessible from world w. That is to say, the state of affairs known as v is a live possibility for w. This gives a pair,.
Next, the frame is extended to a model by specifying the truth-values of all propositions at each of the worlds in G. We do so by defining a relation ⊨ between possible worlds and propositional letters. If there is a world w such that w ⊨ P, then P is true at w. A model is thus an ordered triple,.
Then we recursively define the truth of a formula in a model:
According to these semantics, a truth is necessary with respect to a possible world w if it is true at every world that is accessible to w, and possible if it is true at some world that is accessible to w. Possibility thereby depends upon the accessibility relation R, which allows us to express the relative nature of possibility. For example, we might say that given our laws of physics it is not possible for humans to travel faster than the speed of light, but that given other circumstances it could have been possible to do so. Using the accessibility relation we can translate this scenario as follows: At all of the worlds accessible to our own world, it is not the case that humans can travel faster than the speed of light, but at one of these accessible worlds there is another world accessible from those worlds but not accessible from our own at which humans can travel faster than the speed of light.
It should also be noted that the definition of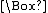 makes vacuously true certain sentences, since when it speaks of "every world that is accesible to w" it takes for granted the usual mathematical interpretation of the word "every" (see vacuous truth
makes vacuously true certain sentences, since when it speaks of "every world that is accesible to w" it takes for granted the usual mathematical interpretation of the word "every" (see vacuous truth
). Hence, if a world w doesn't have any accessible worlds, any sentence beginning with is true.
is true.
The different systems of modal logic are distinguished by the properties of their corresponding accessibility relations. There are several systems that have been espoused (often called frame conditions). An accessibility relation is:
The logics that stem from these frame conditions are:
S5 models are reflexive transitive and euclidean. The accessibility relation R is an equivalence relation. The relation R is reflexive, symmetric and transitive. It is interesting to note how the euclidean property along with reflexivity yields symmetry and transitivity. We can prove that these frames produce the same set of valid sentences as do any frames where all worlds can see all other worlds of W(i.e., where R is a "total" relation). This gives the corresponding modal graph which is total complete (i.e., no more edge (relation) can be added).
For example, in S4:
However, in S5, we can just say that
We can drop the accessibility clause from the latter stipulation because it is trivially true of all S5 frames that w R v.
All of these logical systems can also be defined axiomatically, as is shown in the next section. For example, in S5, the axioms P →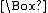
 P,
P, 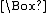 P →
P → 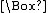
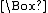 P, and
P, and 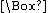 P → P (corresponding to symmetry, transitivity and reflexivity, respectively) hold, whereas at least one of these axioms does not hold in each of the other, weaker logics.
P → P (corresponding to symmetry, transitivity and reflexivity, respectively) hold, whereas at least one of these axioms does not hold in each of the other, weaker logics.
Modern treatments of modal logic begin by augmenting the propositional calculus
with two unary operations, one denoting "necessity" and the other "possibility". The notation of C. I. Lewis
, much employed since, denotes "necessarily p" by a prefixed "box" (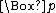 ) whose scope is established by parentheses. Likewise, a prefixed "diamond" (
) whose scope is established by parentheses. Likewise, a prefixed "diamond" ( ) denotes "possibly p". Regardless of notation, each of these operators is definable in terms of the other:
) denotes "possibly p". Regardless of notation, each of these operators is definable in terms of the other:
Hence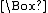 and
and  form a dual pair of operators.
form a dual pair of operators.
In many modal logics, the necessity and possibility operators satisfy the following analogs of de Morgan's laws from Boolean algebra:
Precisely what axioms and rules must be added to the propositional calculus
to create a usable system of modal logic is a matter of philosophical opinion, often driven by the theorems one wishes to prove; or, in computer science, it is a matter of what sort of computational or deductive system one wishes to model. Many modal logics, known collectively as normal modal logic
s, include the following rule and axiom:
The weakest normal modal logic
, named K in honor of Saul Kripke
, is simply the propositional calculus
augmented by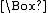 , the rule N, and the axiom K. K is weak in that it fails to determine whether a proposition can be necessary but only contingently necessary. That is, it is not a theorem of K that if
, the rule N, and the axiom K. K is weak in that it fails to determine whether a proposition can be necessary but only contingently necessary. That is, it is not a theorem of K that if 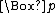 is true then
is true then 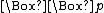 is true, i.e., that necessary truths are "necessarily necessary". If such perplexities are deemed forced and artificial, this defect of K is not a great one. In any case, different answers to such questions yield different systems of modal logic.
is true, i.e., that necessary truths are "necessarily necessary". If such perplexities are deemed forced and artificial, this defect of K is not a great one. In any case, different answers to such questions yield different systems of modal logic.
Adding axioms to K gives rise to other well-known modal systems. One cannot prove in K that if "p is necessary" then p is true. The axiom T remedies this defect:
Other well-known elementary axioms are:
These yield the systems (axioms in bold):
K through S5 form a nested hierarchy of systems, making up the core of normal modal logic
. But specific rules or sets of rules may be appropriate for specific systems. For example, in deontic logic,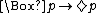 (If it ought to be that p, then it is permitted that p) seems appropriate, but we should probably not include that
(If it ought to be that p, then it is permitted that p) seems appropriate, but we should probably not include that 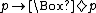 . In fact, to do so is to commit the naturalistic fallacy
. In fact, to do so is to commit the naturalistic fallacy
(i.e. to state that what is natural is also good, by saying that if p is the case, p ought to be permitted).
The commonly employed system S5 simply makes all modal truths necessary. For example, if p is possible, then it is "necessary" that p is possible. Also, if p is necessary, then it is necessary that p is necessary. Other systems of modal logic have been formulated, in part because S5 does not describe every kind of modality of interest.
species. Modal logic was first developed to deal with these concepts, and only afterward was extended to others. For this reason, or perhaps for their familiarity and simplicity, necessity and possibility are often casually treated as the subject matter of modal logic. Moreover it is easier to make sense of relativizing necessity, e.g. to legal, physical, nomological, epistemic, and so on, than it is to make sense of relativizing other notions.
In classical modal logic
, a proposition is said to be
In classical modal logic, therefore, either the notion of possibility or necessity may be taken to be basic, where these other notions are defined in terms of it in the manner of De Morgan duality. Intuitionistic modal logic treats possibility and necessity as not perfectly symmetric.
For those with difficulty with the concept of something being possible but not true, the meaning of these terms may be made more comprehensible by thinking of multiple "possible worlds" (in the sense of Leibniz) or "alternate universes"; something "necessary" is true in all possible worlds, something "possible" is true in at least one possible world. These "possible world semantics" are formalized with Kripke semantics
.
. For example, current theory allows for there to be an atom
with an atomic number
of 150, though there may not in fact be any such atoms in existence. Similarly, while it is logically possible to accelerate beyond the speed of light
, modern science stipulates that it is not physically possible for material particles or information.
. Saul Kripke
has argued that every person necessarily has the parents they do have: anyone with different parents would not be the same person.
Metaphysical possibility is generally thought to be more restricting than bare logical possibility (i.e., fewer things are metaphysically possible than are logically possible). Its exact relation to physical possibility is a matter of some dispute. Philosophers also disagree over whether metaphysical truths are necessary merely "by definition", or whether they reflect some underlying deep facts about the world, or something else entirely.
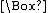 operator is translated as "x knows that…", and the
operator is translated as "x knows that…", and the  operator is translated as "For all x knows, it may be true that…" In ordinary speech both metaphysical and epistemic modalities are often expressed in similar words; the following contrasts may help:
operator is translated as "For all x knows, it may be true that…" In ordinary speech both metaphysical and epistemic modalities are often expressed in similar words; the following contrasts may help:
A person, Jones, might reasonably say both: (1) "No, it is not possible that Bigfoot
exists; I am quite certain of that"; and, (2) "Sure, Bigfoot possibly could exist". What Jones means by (1) is that given all the available information, there is no question remaining as to whether Bigfoot exists. This is an epistemic claim. By (2) he makes the metaphysical claim that it is possible for Bigfoot to exist, even though he does not (which is not equivalent to "it is possible that Bigfoot exists – for all I know", which contradicts (1)).
From the other direction, Jones might say, (3) "It is possible that Goldbach's conjecture
is true; but also possible that it is false", and also (4) "if it is true, then it is necessarily true, and not possibly false". Here Jones means that it is epistemically possible that it is true or false, for all he knows (Goldbach's conjecture has not been proven either true or false), but if there is a proof (heretofore undiscovered), then it would show that it is not logically possible for Goldbach's conjecture to be false—there could be no set of numbers that violated it. Logical possibility is a form of alethic possibility; (4) makes a claim about whether it is possible (i.e., logically speaking) that a mathematical truth to have been false, but (3) only makes a claim about whether it is possible, for all Jones knows, (i.e., speaking of certitude) that the mathematical claim is specifically either true or false, and so again Jones does not contradict himself. It is worthwhile to observe that Jones is not necessarily correct: It is possible (epistemically) that Goldbach's conjecture is both true and unprovable.
Epistemic possibilities also bear on the actual world in a way that metaphysical possibilities do not. Metaphysical possibilities bear on ways the world might have been, but epistemic possibilities bear on the way the world may be (for all we know). Suppose, for example, that I want to know whether or not to take an umbrella before I leave. If you tell me "it is possible that it is raining outside" – in the sense of epistemic possibility – then that would weigh on whether or not I take the umbrella. But if you just tell me that "it is possible for it to rain outside" – in the sense of metaphysical possibility – then I am no better off for this bit of modal enlightenment.
Some features of epistemic modal logic are in debate. For example, if x knows that p, does x know that it knows that p? That is to say, should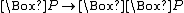 be an axiom in these systems? While the answer to this question is unclear, there is at least one axiom that must be included in epistemic modal logic, because it is minimally true of all modal logics (see the section on axiomatic systems):
be an axiom in these systems? While the answer to this question is unclear, there is at least one axiom that must be included in epistemic modal logic, because it is minimally true of all modal logics (see the section on axiomatic systems):
But this is disconcerting, because with K, we can prove that we know all the logical consequences of our beliefs: If q is a logical consequence of p, then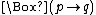 . And if so, then we can deduce that
. And if so, then we can deduce that 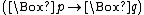 using K. When we translate this into epistemic terms, this says that if q is a logical consequence of p, then we know that it is, and if we know p, we know q. That is to say, we know all the logical consequences of our beliefs. This must be true for all possible Kripkean
using K. When we translate this into epistemic terms, this says that if q is a logical consequence of p, then we know that it is, and if we know p, we know q. That is to say, we know all the logical consequences of our beliefs. This must be true for all possible Kripkean
modal interpretations of epistemic cases where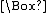 is translated as "knows that". But then, for example, if x knows that prime numbers are divisible only by themselves and the number one, then x knows that 8683317618811886495518194401279999999 is prime (since this number is only divisible by itself and the number one). That is to say, under the modal interpretation of knowledge, anyone who knows the definition of a prime number knows that this number is prime. This shows that epistemic modal logic is an idealized account of knowledge, and explains objective, rather than subjective knowledge (if anything).
is translated as "knows that". But then, for example, if x knows that prime numbers are divisible only by themselves and the number one, then x knows that 8683317618811886495518194401279999999 is prime (since this number is only divisible by itself and the number one). That is to say, under the modal interpretation of knowledge, anyone who knows the definition of a prime number knows that this number is prime. This shows that epistemic modal logic is an idealized account of knowledge, and explains objective, rather than subjective knowledge (if anything).
, that is, expressions with qualifications of when. Some expressions, such as '2 + 2 = 4', are true at all times, while tensed expressions such as 'John is happy' are only true sometimes.
In temporal logic, tense constructions are treated in terms of modalities, where a standard method for formalizing talk of time is to use two pairs of operators, one for the past and one for the future (P will just mean 'it is presently the case that P'). For example:
There are then at least three modal logics that we can develop. For example, we can stipulate that,
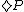 = P is the case at some time t
= P is the case at some time t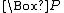 = P is the case at every time t
= P is the case at every time t
Or we can trade these operators to deal only with the future (or past). For example,
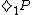 = FP
= FP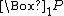 = GP
= GP
or,
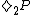 = P and/or FP
= P and/or FP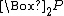 = P and GP
= P and GP
The operators F and G may seem initially foreign, but they create normal modal systems
. Note that FP is the same as ¬G¬P. We can combine the above operators to form complex statements. For example, PP →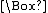 PP says (effectively), Everything that is past and true is necessary.
PP says (effectively), Everything that is past and true is necessary.
It seems reasonable to say that possibly it will rain tomorrow, and possibly it won't; on the other hand, seeing as how we can't change the past, if it is true that it rained yesterday, it probably isn't true that it may not have rained yesterday. It seems the past is "fixed", or necessary, in a way the future is not. This is sometimes referred to as accidental necessity
. But if the past is "fixed", and everything that is in the future will eventually be in the past, then it seems plausible to say that future events are necessary too.
Similarly, the problem of future contingents considers the semantics of assertions about the future: is either of the propositions 'There will be a sea battle tomorrow', or 'There will not be a sea battle tomorrow' now true? Considering this thesis led Aristotle
to reject the principle of bivalence
for assertions concerning the future.
Additional binary operators are also relevant to temporal logics, q.v. Linear Temporal Logic
.
Versions of temporal logic can be used in computer science
to model computer operations and prove theorems about them. In one version,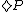 means "at a future time in the computation it is possible that the computer state will be such that P is true";
means "at a future time in the computation it is possible that the computer state will be such that P is true"; 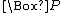 means "at all future times in the computation P will be true". In another version,
means "at all future times in the computation P will be true". In another version, 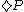 means "at the immediate next state of the computation, P might be true";
means "at the immediate next state of the computation, P might be true"; 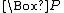 means "at the immediate next state of the computation, P will be true". These differ in the choice of Accessibility relation
means "at the immediate next state of the computation, P will be true". These differ in the choice of Accessibility relation
. (P always means "P is true at the current computer state".) These two examples involve nondeterministic or not-fully-understood computations; there are many other modal logics specialized to different types of program analysis. Each one naturally leads to slightly different axioms.
A variation, closely related to Temporal or Chronological or Tense logics, are Modal logics based upon "topology", "place", or "spatial position". One might also take note that in the Russian language, verbs have an aspect, based commonly upon time, but position also.
and norms
generally, seems to have a modal structure. The difference between "You must do this" and "You may do this" looks a lot like the difference between "This is necessary" and "This is possible". Such logics are called deontic
, from the Greek for "duty".
Deontic logics commonly lack the axiom T semantically corresponding to the reflexivity of the accessibility relation in Kripke semantics
: in symbols,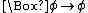 . Interpreting
. Interpreting 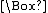 as "it is obligatory that", T informally says that every obligation is true. For example, if it is obligatory not to kill others (i.e. killing is morally forbidden), then T implies that people actually do not kill others. The consequent is obviously false.
as "it is obligatory that", T informally says that every obligation is true. For example, if it is obligatory not to kill others (i.e. killing is morally forbidden), then T implies that people actually do not kill others. The consequent is obviously false.
Instead, using Kripke semantics
, we say that though our own world does not realize all obligations, the worlds accessible to it do (i.e., T holds at these worlds). These worlds are called idealized worlds. P is obligatory with respect to our own world if at all idealized worlds accessible to our world, P holds. Though this was one of the first interpretations of the formal semantics, it has recently come under criticism.
One other principle that is often (at least traditionally) accepted as a deontic principle is D,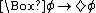 , which corresponds to the seriality (or extendability or unboundedness) of the accessibility relation. It is an embodiment of the Kantian idea that "ought implies can". (Clearly the "can" can be interpreted in various senses, e.g. in a moral or alethic sense.)
, which corresponds to the seriality (or extendability or unboundedness) of the accessibility relation. It is an embodiment of the Kantian idea that "ought implies can". (Clearly the "can" can be interpreted in various senses, e.g. in a moral or alethic sense.)
But (1) says that if you have killed the victim, then it ought to be the case that you have killed him quickly. This surely isn't right, because you ought not to have killed him at all. And (2) doesn't work either. If the right representation of "if you have killed the victim then you ought to have killed him quickly" is (2), then the right representation of (3) "if you have killed the victim then you ought to have killed him slowly" is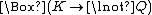 . Now suppose (as seems reasonable) that you should not have killed the victim, or
. Now suppose (as seems reasonable) that you should not have killed the victim, or 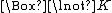 . But then we can deduce
. But then we can deduce 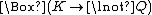 , which would express sentence (3). So if you should not have killed the victim, then if you did kill him, you should have killed him slowly. But that can't be right, and is not right when we use natural language. Telling someone they should not kill the victim certainly does not imply that they should kill the victim slowly if they do kill him.
, which would express sentence (3). So if you should not have killed the victim, then if you did kill him, you should have killed him slowly. But that can't be right, and is not right when we use natural language. Telling someone they should not kill the victim certainly does not imply that they should kill the victim slowly if they do kill him.
doxa which means "belief". Typically, a doxastic logic uses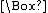 , often written "B", to mean "It is believed that", or when relativized to a particular agent s, "It is believed by s that".
, often written "B", to mean "It is believed that", or when relativized to a particular agent s, "It is believed by s that".
, then it is a necessary truth. If a statement happens to be true in our world, but is not true in all possible worlds, then it is a contingent truth. A statement that is true in some possible world (not necessarily our own) is called a possible truth.
Under this "possible worlds idiom," to maintain that Bigfoot's existence is possible but not actual, one says, "There is some possible world in which Bigfoot exists; but in the actual world, Bigfoot does not exist". However, it is unclear what this claim commits us to. Are we really alleging the existence of possible worlds, every bit as real as our actual world, just not actual? Saul Kripke
believes that 'possible world' is something of a misnomer – that the term 'possible world' is just a useful way of visualizing the concept of possibility. For him, the sentences "you could have rolled a 4 instead of a 6" and "there is a possible world where you rolled a 4, but you rolled a 6 in the actual world" are not significantly different statements, and neither commit us to the existence of a possible world. David Lewis, on the other hand, made himself notorious by biting the bullet, asserting that all merely possible worlds are as real as our own, and that what distinguishes our world as actual is simply that it is indeed our world – this
world. That position is a major tenet of "modal realism
". Some philosophers decline to endorse any version of modal realism, considering it ontologically extravagant, and prefer to seek various ways to paraphrase away these ontological commitments. Robert Adams holds that 'possible worlds' are better thought of as 'world-stories', or consistent sets of propositions. Thus, it is possible that you rolled a 4 if such a state of affairs can be described coherently.
Computer scientists will generally pick a highly specific interpretation of the modal operators specialized to the particular sort of computation being analysed. In place of "all worlds", you may have "all possible next states of the computer", or "all possible future states of the computer".
As an example, consider the following context-sensitive grammar for an alethic Modal logic grammar:
L=({S, X, R, M}, {Φ,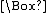 ,
,  , , &,
, , &,  , &, v, ~}, P, S), where Φ is a meta-variable for propositions, and P are the following production rules:
, &, v, ~}, P, S), where Φ is a meta-variable for propositions, and P are the following production rules:
S XR | M
XR | M
XR
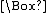 M |
M |  M
M
M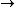 T M | T
T M | T
T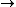 (T
(T 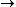 T) | (T & T) | (T v T) | (~T) | Φ
T) | (T & T) | (T v T) | (~T) | Φ
A sample derivation:
S XR
XR 
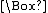 M
M 
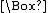 T
T 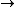
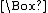 ( T & T )
( T & T ) 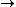
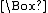 ( Φ & T )
( Φ & T ) 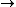
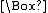 ( p & T )
( p & T ) 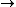
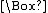 ( p & Φ )
( p & Φ ) 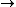
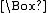 ( p & q )
( p & q )
Of course, an equivalent context-free language is easy to construct, but the point here is that a Modal logic based upon a context-sensitive grammar is possible. More complex Modal logics which are Chomsky type-0 or type-1 extends the philosophical discussion of Modal logics.
Thus, for example, the following might be persuasive rhetorically:
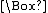 (p & q)
(p & q)
______________________________
Therefore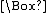 p
p
but ~[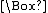 (p & q)
(p & q) 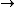 (
(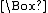 p &
p & 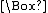 q) ]
q) ]
has pointed out how radically conservative were the views of Bertrand Russell
in his unreasoned rejection of both Modal Logic and the ideas of the philosopher Alexius Meinong
. Indeed, Arthur Norman Prior warned his protégé Ruth Barcan to prepare well in the debates concerning Modal Logic (with Willard Van Orman Quine
) due to the biases against Modal Logic.
Predicate logic
In mathematical logic, predicate logic is the generic term for symbolic formal systems like first-order logic, second-order logic, many-sorted logic or infinitary logic. This formal system is distinguished from other systems in that its formulae contain variables which can be quantified...
to include operators expressing modality
Linguistic modality
In linguistics, modality is what allows speakers to evaluate a proposition relative to a set of other propositions.In standard formal approaches to modality, an utterance expressing modality can always roughly be paraphrased to fit the following template:...
. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is usually happy, in which case the term "usually" is functioning as a modal. The traditional alethic modalities
Alethic modality
Alethic modality is a linguistic modality which indicates logical necessity, possibility or impossibility.Alethic modality is often associated with epistemic modality in research. However, it has been questioned whether this modality should be considered distinct from epistemic modality which...
, or modalities of truth, include possibility
Logical possibility
A logically possible proposition is one that can be asserted without implying a logical contradiction. This is to say that a proposition is logically possible if there is some coherent way for the world to be, under which the proposition would be true...
("Possibly, p", "It is possible that p"), necessity ("Necessarily, p", "It is necessary that p"), and impossibility ("It is impossible that p"). Other modalities that have been formalized in modal logic include temporal
Temporal
Temporal can refer to:* of or relating to time** Temporality in philosophy** Temporal database, a database recording aspects of time varying values** The Temporal power of the Popes of the Roman Catholic Church...
modalities, or modalities or time (notably, "It was the case that p", "It has always been that p", "It will be that p", "It will always be that p"), deontic modalities (notably, "It is obligatory that p", and "It is permissible that p"), epistemic modalities, or modalities of knowledge ("It is known that p") and doxastic modalities, or modalities of belief ("It is believed that p").
A formal modal logic represents modalities using modal operator
Modal operator
In modal logic, a modal operator is an operator which forms propositions from propositions. In general, a modal operator has the "formal" property of being non-truth-functional, and is "intuitively" characterised by expressing a modal attitude about the proposition to which the operator is applied...
s. For example, "It might rain today" and "It is possible that rain will fall today" both contain the notion of possibility. In a modal logic this is represented as an operator, Possibly, attached to the sentence "It will rain today".
The basic unary
Unary operation
In mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a functionf:\ A\to Awhere A is a set. In this case f is called a unary operation on A....
(1-place) modal operators are usually written
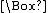 for Necessarily and
for Necessarily and  for Possibly. In a classical modal logic
for Possibly. In a classical modal logicClassical modal logic
In modal logic, a classical modal logic L is any modal logic containing the duality of the modal operators\Diamond A \equiv \lnot\Box\lnot Awhich is also closed under the rule A \equiv B \vdash \Box A\equiv\Box B....
, each can be expressed by the other with negation
Negation
In logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified...
:
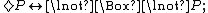
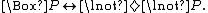
Thus it is possible that it will rain today if and only if it is not necessary that it will not rain today;
and it is necessary that it will rain today if and only if it is not possible that it will not rain today.
Development of modal logic
Although AristotleAristotle
Aristotle was a Greek philosopher and polymath, a student of Plato and teacher of Alexander the Great. His writings cover many subjects, including physics, metaphysics, poetry, theater, music, logic, rhetoric, linguistics, politics, government, ethics, biology, and zoology...
's logic is almost entirely concerned with the theory of the categorical syllogism, there are passages in his work, such as the famous sea-battle argument in De Interpretatione § 9, that are now seen as anticipations of modal logic and its connection with potentiality and time. Modal logic as a self-aware subject owes much to the writings of the Scholastics, in particular William of Ockham
William of Ockham
William of Ockham was an English Franciscan friar and scholastic philosopher, who is believed to have been born in Ockham, a small village in Surrey. He is considered to be one of the major figures of medieval thought and was at the centre of the major intellectual and political controversies of...
and John Duns Scotus, who reasoned informally in a modal manner, mainly to analyze statements about essence
Essence
In philosophy, essence is the attribute or set of attributes that make an object or substance what it fundamentally is, and which it has by necessity, and without which it loses its identity. Essence is contrasted with accident: a property that the object or substance has contingently, without...
and accident
Accident (philosophy)
Accident, as used in philosophy, is an attribute which may or may not belong to a subject, without affecting its essence. The word "accident" has been employed throughout the history of philosophy with several distinct meanings....
.
C. I. Lewis founded modern modal logic in his 1910 Harvard thesis and in a series of scholarly articles beginning in 1912. This work culminated in his 1932 book Symbolic Logic (with C. H. Langford), which introduced the five systems S1 through S5.
Ruth C. Barcan (later Ruth Barcan Marcus
Ruth Barcan Marcus
Ruth Barcan Marcus is the American philosopher and logician after whom the Barcan formula is named. She is a pioneering figure in the quantification of modal logic and the theory of direct reference...
) developed the first axiomatic systems of quantified modal logic — first and second order extensions of Lewis's "S2", "S4", and "S5".
The contemporary era in modal semantics began in 1959, when Saul Kripke
Saul Kripke
Saul Aaron Kripke is an American philosopher and logician. He is a professor emeritus at Princeton and teaches as a Distinguished Professor of Philosophy at the CUNY Graduate Center...
(then only a 19-year-old Harvard University
Harvard University
Harvard University is a private Ivy League university located in Cambridge, Massachusetts, United States, established in 1636 by the Massachusetts legislature. Harvard is the oldest institution of higher learning in the United States and the first corporation chartered in the country...
undergraduate) introduced the now-standard Kripke semantics
Kripke semantics
Kripke semantics is a formal semantics for non-classical logic systems created in the late 1950s and early 1960s by Saul Kripke. It was first made for modal logics, and later adapted to intuitionistic logic and other non-classical systems...
for modal logics. These are commonly referred to as "possible worlds" semantics. Kripke and A. N. Prior had previously corresponded at some length. Kripke semantics is basically simple, but proofs are eased using semantic-tableaus or analytic tableaux, as explained by E. W. Beth.
A. N. Prior created modern temporal logic
Temporal logic
In logic, the term temporal logic is used to describe any system of rules and symbolism for representing, and reasoning about, propositions qualified in terms of time. In a temporal logic we can then express statements like "I am always hungry", "I will eventually be hungry", or "I will be hungry...
, closely related to modal logic, in 1957 by adding modal operators [F] and [P] meaning "henceforth" and "hitherto". Vaughan Pratt introduced dynamic logic
Dynamic logic (modal logic)
Dynamic logic is an extension of modal logic originally intended for reasoning about computer programs and later applied to more general complex behaviors arising in linguistics, philosophy, AI, and other fields.-Language:...
in 1976. In 1977, Amir Pnueli proposed using temporal logic to formalise the behaviour of continually operating concurrent programs. Flavors of temporal logic include propositional dynamic logic (PDL), propositional linear temporal logic (PLTL), linear temporal logic
Linear temporal logic
In logic, Linear temporal logic is a modal temporal logic with modalities referring to time. In LTL, one can encode formulae about the future of paths such as that a condition will eventually be true, that a condition will be true until another fact becomes true, etc. It is a fragment of the more...
(LTL), computational tree logic
Computational tree logic
Computation tree logic is a branching-time logic, meaning that its model of time is a tree-like structure in which the future is not determined; there are different paths in the future, any one of which might be an actual path that is realised...
(CTL), Hennessy–Milner logic
Hennessy-Milner logic
In computer science, Hennessy–Milner logic is a multimodal logic used to specify properties of a labeled transition system, a structure similar to an automaton...
, and T.
The mathematical structure of modal logic, namely Boolean algebras augmented with unary operation
Unary operation
In mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a functionf:\ A\to Awhere A is a set. In this case f is called a unary operation on A....
s (often called modal algebra
Modal algebra
In algebra and logic, a modal algebra is a structure \langle A,\land,\lor,-,0,1,\Box\rangle such that*\langle A,\land,\lor,-,0,1\rangle is a Boolean algebra,...
s), began to emerge with J. C. C. McKinsey's 1941 proof that S2 and S4 are decidable, and reached full flower in the work of Alfred Tarski
Alfred Tarski
Alfred Tarski was a Polish logician and mathematician. Educated at the University of Warsaw and a member of the Lwow-Warsaw School of Logic and the Warsaw School of Mathematics and philosophy, he emigrated to the USA in 1939, and taught and carried out research in mathematics at the University of...
and his student Bjarni Jonsson
Bjarni Jónsson
Bjarni Jónsson is an Icelandic mathematician and logician working in universal algebra and lattice theory. He is emeritus Distinguished Professor of Mathematics at Vanderbilt University and the honorary editor in chief of Algebra Universalis...
(Jonsson and Tarski 1951–52). This work revealed that S4 and S5 are models of interior algebra
Interior algebra
In abstract algebra, an interior algebra is a certain type of algebraic structure that encodes the idea of the topological interior of a set. Interior algebras are to topology and the modal logic S4 what Boolean algebras are to set theory and ordinary propositional logic...
, a proper extension of Boolean algebra originally designed to capture the properties of the interior and closure operator
Closure operator
In mathematics, a closure operator on a set S is a function cl: P → P from the power set of S to itself which satisfies the following conditions for all sets X,Y ⊆ S....
s of topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
. Texts on modal logic typically do little more than mention its connections with the study of Boolean algebras and topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
. For a thorough survey of the history of formal modal logic and of the associated mathematics, see http://www.mcs.vuw.ac.nz/~rob/papers/modalhist.pdfRobert Goldblatt
Robert Goldblatt
Robert Ian Goldblatt is a mathematical logician at the School of Mathematics, Statistics and Operations Research at Victoria University, Wellington, New Zealand, and a member of the Centre for Logic, Language and Computation. His academic academic genealogy can be traced back to Leibniz...
(2006).]
Semantics
The semantics for modal logic are usually given like so:First we define a frame, which consists of a non-empty set, G, whose members are generally called possible worlds, and a binary relation, R, that holds (or not) between the possible worlds of G. This binary relation is called the accessibility relation
Accessibility relation
In modal logic, an accessibility relation is a binary relation, written as R\,\! between possible worlds.-Description of terms:A statement in logic refers to a sentence that can be true or false...
. For example, w R v means that the world v is accessible from world w. That is to say, the state of affairs known as v is a live possibility for w. This gives a pair,
Next, the frame is extended to a model by specifying the truth-values of all propositions at each of the worlds in G. We do so by defining a relation ⊨ between possible worlds and propositional letters. If there is a world w such that w ⊨ P, then P is true at w. A model is thus an ordered triple,
Then we recursively define the truth of a formula in a model:
- w ⊨ ¬P if and only if w
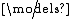 P
P - w ⊨ (P
 Q) if and only if w ⊨ P and w ⊨ Q
Q) if and only if w ⊨ P and w ⊨ Q - w ⊨
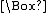 P if and only if for every element v of G, if w R v then v ⊨ P
P if and only if for every element v of G, if w R v then v ⊨ P - w ⊨
 P if and only if for some element v of G, it holds that w R v and v ⊨ P
P if and only if for some element v of G, it holds that w R v and v ⊨ P
According to these semantics, a truth is necessary with respect to a possible world w if it is true at every world that is accessible to w, and possible if it is true at some world that is accessible to w. Possibility thereby depends upon the accessibility relation R, which allows us to express the relative nature of possibility. For example, we might say that given our laws of physics it is not possible for humans to travel faster than the speed of light, but that given other circumstances it could have been possible to do so. Using the accessibility relation we can translate this scenario as follows: At all of the worlds accessible to our own world, it is not the case that humans can travel faster than the speed of light, but at one of these accessible worlds there is another world accessible from those worlds but not accessible from our own at which humans can travel faster than the speed of light.
It should also be noted that the definition of
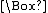 makes vacuously true certain sentences, since when it speaks of "every world that is accesible to w" it takes for granted the usual mathematical interpretation of the word "every" (see vacuous truth
makes vacuously true certain sentences, since when it speaks of "every world that is accesible to w" it takes for granted the usual mathematical interpretation of the word "every" (see vacuous truthVacuous truth
A vacuous truth is a truth that is devoid of content because it asserts something about all members of a class that is empty or because it says "If A then B" when in fact A is inherently false. For example, the statement "all cell phones in the room are turned off" may be true...
). Hence, if a world w doesn't have any accessible worlds, any sentence beginning with
 is true.
is true.The different systems of modal logic are distinguished by the properties of their corresponding accessibility relations. There are several systems that have been espoused (often called frame conditions). An accessibility relation is:
- reflexive iff w R w, for every w in G
- symmetric iff w R v implies v R w, for all w and v in G
- transitive iff w R v and v R q together imply w R q, for all w, v, q in G.
- serial iff, for each w in G there is some v in G such that w R v.
- euclidean iff, for every u,v and w, u R w and v R w implies u R v (note that it also implies: v R u)
The logics that stem from these frame conditions are:
- K := no conditions
- D := serial
- T := reflexive
- S4 := reflexive and transitive
- S5 := reflexive, symmetric, transitive and Euclidean
S5 models are reflexive transitive and euclidean. The accessibility relation R is an equivalence relation. The relation R is reflexive, symmetric and transitive. It is interesting to note how the euclidean property along with reflexivity yields symmetry and transitivity. We can prove that these frames produce the same set of valid sentences as do any frames where all worlds can see all other worlds of W(i.e., where R is a "total" relation). This gives the corresponding modal graph which is total complete (i.e., no more edge (relation) can be added).
For example, in S4:
-
- w ⊨
 P if and only if for some element v of G, it holds that v ⊨ P and w R v.
P if and only if for some element v of G, it holds that v ⊨ P and w R v.
- w ⊨
However, in S5, we can just say that
-
- w ⊨
 P if and only if for some element v of G, it holds that v ⊨ P.
P if and only if for some element v of G, it holds that v ⊨ P.
- w ⊨
We can drop the accessibility clause from the latter stipulation because it is trivially true of all S5 frames that w R v.
All of these logical systems can also be defined axiomatically, as is shown in the next section. For example, in S5, the axioms P →
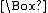
 P,
P, 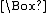 P →
P → 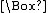
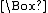 P, and
P, and 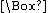 P → P (corresponding to symmetry, transitivity and reflexivity, respectively) hold, whereas at least one of these axioms does not hold in each of the other, weaker logics.
P → P (corresponding to symmetry, transitivity and reflexivity, respectively) hold, whereas at least one of these axioms does not hold in each of the other, weaker logics.Axiomatic systems
The first formalizations of modal logic were axiomatic. Numerous variations with very different properties have been proposed since C. I. Lewis began working in the area in 1910. Hughes and Cresswell (1996), for example, describe 42 normal and 25 non-normal modal logics. Zeman (1973) describes some systems Hughes and Cresswell omit.Modern treatments of modal logic begin by augmenting the propositional calculus
Propositional calculus
In mathematical logic, a propositional calculus or logic is a formal system in which formulas of a formal language may be interpreted as representing propositions. A system of inference rules and axioms allows certain formulas to be derived, called theorems; which may be interpreted as true...
with two unary operations, one denoting "necessity" and the other "possibility". The notation of C. I. Lewis
Clarence Irving Lewis
Clarence Irving Lewis , usually cited as C. I. Lewis, was an American academic philosopher and the founder of conceptual pragmatism. First a noted logician, he later branched into epistemology, and during the last 20 years of his life, he wrote much on ethics.-Early years:Lewis was born in...
, much employed since, denotes "necessarily p" by a prefixed "box" (
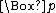 ) whose scope is established by parentheses. Likewise, a prefixed "diamond" (
) whose scope is established by parentheses. Likewise, a prefixed "diamond" (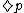 ) denotes "possibly p". Regardless of notation, each of these operators is definable in terms of the other:
) denotes "possibly p". Regardless of notation, each of these operators is definable in terms of the other:
-
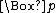 (necessarily p) is equivalent to
(necessarily p) is equivalent to 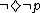 ("not possible that not-p")
("not possible that not-p") -
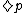 (possibly p) is equivalent to
(possibly p) is equivalent to 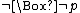 ("not necessarily not-p")
("not necessarily not-p")
Hence
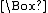 and
and  form a dual pair of operators.
form a dual pair of operators.In many modal logics, the necessity and possibility operators satisfy the following analogs of de Morgan's laws from Boolean algebra:
- "It is not necessary that X" is logically equivalentLogical equivalenceIn logic, statements p and q are logically equivalent if they have the same logical content.Syntactically, p and q are equivalent if each can be proved from the other...
to "It is possible that not X".
- "It is not possible that X" is logically equivalent to "It is necessary that not X".
Precisely what axioms and rules must be added to the propositional calculus
Propositional calculus
In mathematical logic, a propositional calculus or logic is a formal system in which formulas of a formal language may be interpreted as representing propositions. A system of inference rules and axioms allows certain formulas to be derived, called theorems; which may be interpreted as true...
to create a usable system of modal logic is a matter of philosophical opinion, often driven by the theorems one wishes to prove; or, in computer science, it is a matter of what sort of computational or deductive system one wishes to model. Many modal logics, known collectively as normal modal logic
Normal modal logic
In logic, a normal modal logic is a set L of modal formulas such that L contains:* All propositional tautologies;* All instances of the Kripke schema: \Box\toand it is closed under:...
s, include the following rule and axiom:
- N, Necessitation Rule: If p is a theoremTheoremIn mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
(of any system invoking N), then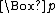 is likewise a theorem.
is likewise a theorem. - K, Distribution Axiom:
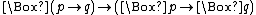 .
.
The weakest normal modal logic
Normal modal logic
In logic, a normal modal logic is a set L of modal formulas such that L contains:* All propositional tautologies;* All instances of the Kripke schema: \Box\toand it is closed under:...
, named K in honor of Saul Kripke
Saul Kripke
Saul Aaron Kripke is an American philosopher and logician. He is a professor emeritus at Princeton and teaches as a Distinguished Professor of Philosophy at the CUNY Graduate Center...
, is simply the propositional calculus
Propositional calculus
In mathematical logic, a propositional calculus or logic is a formal system in which formulas of a formal language may be interpreted as representing propositions. A system of inference rules and axioms allows certain formulas to be derived, called theorems; which may be interpreted as true...
augmented by
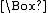 , the rule N, and the axiom K. K is weak in that it fails to determine whether a proposition can be necessary but only contingently necessary. That is, it is not a theorem of K that if
, the rule N, and the axiom K. K is weak in that it fails to determine whether a proposition can be necessary but only contingently necessary. That is, it is not a theorem of K that if 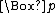 is true then
is true then 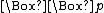 is true, i.e., that necessary truths are "necessarily necessary". If such perplexities are deemed forced and artificial, this defect of K is not a great one. In any case, different answers to such questions yield different systems of modal logic.
is true, i.e., that necessary truths are "necessarily necessary". If such perplexities are deemed forced and artificial, this defect of K is not a great one. In any case, different answers to such questions yield different systems of modal logic.Adding axioms to K gives rise to other well-known modal systems. One cannot prove in K that if "p is necessary" then p is true. The axiom T remedies this defect:
- T, Reflexivity Axiom:
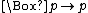 (If p is necessary, then p is the case.) T holds in most but not all modal logics. Zeman (1973) describes a few exceptions, such as S10.
(If p is necessary, then p is the case.) T holds in most but not all modal logics. Zeman (1973) describes a few exceptions, such as S10.
Other well-known elementary axioms are:
- 4:
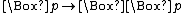
- B:
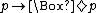
- D:
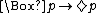
- 5:
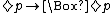
These yield the systems (axioms in bold):
- K := K + N
- T := K + T
- S4 := T + 4
- S5 := S4 + 5
- D := K + D.
K through S5 form a nested hierarchy of systems, making up the core of normal modal logic
Normal modal logic
In logic, a normal modal logic is a set L of modal formulas such that L contains:* All propositional tautologies;* All instances of the Kripke schema: \Box\toand it is closed under:...
. But specific rules or sets of rules may be appropriate for specific systems. For example, in deontic logic,
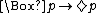 (If it ought to be that p, then it is permitted that p) seems appropriate, but we should probably not include that
(If it ought to be that p, then it is permitted that p) seems appropriate, but we should probably not include that 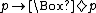 . In fact, to do so is to commit the naturalistic fallacy
. In fact, to do so is to commit the naturalistic fallacyNaturalistic fallacy
The naturalistic fallacy is often claimed to be a formal fallacy. It was described and named by British philosopher G. E. Moore in his 1903 book Principia Ethica...
(i.e. to state that what is natural is also good, by saying that if p is the case, p ought to be permitted).
The commonly employed system S5 simply makes all modal truths necessary. For example, if p is possible, then it is "necessary" that p is possible. Also, if p is necessary, then it is necessary that p is necessary. Other systems of modal logic have been formulated, in part because S5 does not describe every kind of modality of interest.
Alethic logic
Modalities of necessity and possibility are called alethic modalities. They are also sometimes called special modalities, from the LatinLatin
Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
species. Modal logic was first developed to deal with these concepts, and only afterward was extended to others. For this reason, or perhaps for their familiarity and simplicity, necessity and possibility are often casually treated as the subject matter of modal logic. Moreover it is easier to make sense of relativizing necessity, e.g. to legal, physical, nomological, epistemic, and so on, than it is to make sense of relativizing other notions.
In classical modal logic
Classical modal logic
In modal logic, a classical modal logic L is any modal logic containing the duality of the modal operators\Diamond A \equiv \lnot\Box\lnot Awhich is also closed under the rule A \equiv B \vdash \Box A\equiv\Box B....
, a proposition is said to be
- possible if and only if it is not necessarily false (regardless of whether it is actually true or actually false);
- necessary if and only if it is not possibly false; and
- contingent if and only if it is not necessarily false and not necessarily true (i.e. possible but not necessarily true).
In classical modal logic, therefore, either the notion of possibility or necessity may be taken to be basic, where these other notions are defined in terms of it in the manner of De Morgan duality. Intuitionistic modal logic treats possibility and necessity as not perfectly symmetric.
For those with difficulty with the concept of something being possible but not true, the meaning of these terms may be made more comprehensible by thinking of multiple "possible worlds" (in the sense of Leibniz) or "alternate universes"; something "necessary" is true in all possible worlds, something "possible" is true in at least one possible world. These "possible world semantics" are formalized with Kripke semantics
Kripke semantics
Kripke semantics is a formal semantics for non-classical logic systems created in the late 1950s and early 1960s by Saul Kripke. It was first made for modal logics, and later adapted to intuitionistic logic and other non-classical systems...
.
Physical possibility
Something is physically possible if it is permitted by the laws of physicsPhysical law
A physical law or scientific law is "a theoretical principle deduced from particular facts, applicable to a defined group or class of phenomena, and expressible by the statement that a particular phenomenon always occurs if certain conditions be present." Physical laws are typically conclusions...
. For example, current theory allows for there to be an atom
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
with an atomic number
Atomic number
In chemistry and physics, the atomic number is the number of protons found in the nucleus of an atom and therefore identical to the charge number of the nucleus. It is conventionally represented by the symbol Z. The atomic number uniquely identifies a chemical element...
of 150, though there may not in fact be any such atoms in existence. Similarly, while it is logically possible to accelerate beyond the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
, modern science stipulates that it is not physically possible for material particles or information.
Metaphysical possibility
Philosophers ponder the properties that objects have independently of those dictated by scientific laws. For example, it might be metaphysically necessary, as some have thought, that all thinking beings have bodies and can experience the passage of timeTime
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
. Saul Kripke
Saul Kripke
Saul Aaron Kripke is an American philosopher and logician. He is a professor emeritus at Princeton and teaches as a Distinguished Professor of Philosophy at the CUNY Graduate Center...
has argued that every person necessarily has the parents they do have: anyone with different parents would not be the same person.
Metaphysical possibility is generally thought to be more restricting than bare logical possibility (i.e., fewer things are metaphysically possible than are logically possible). Its exact relation to physical possibility is a matter of some dispute. Philosophers also disagree over whether metaphysical truths are necessary merely "by definition", or whether they reflect some underlying deep facts about the world, or something else entirely.
Confusion with epistemic modalities
Alethic modalities and epistemic modalities (see below) are often expressed in English using the same words. "It is possible that bigfoot exists" can mean either "Bigfoot could exist, whether or not bigfoot does in fact exist" (alethic), or more likely, "For all I know, bigfoot exists" (epistemic).Epistemic logic
Epistemic modalities (from the Greek episteme, knowledge), deal with the certainty of sentences. The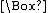 operator is translated as "x knows that…", and the
operator is translated as "x knows that…", and the  operator is translated as "For all x knows, it may be true that…" In ordinary speech both metaphysical and epistemic modalities are often expressed in similar words; the following contrasts may help:
operator is translated as "For all x knows, it may be true that…" In ordinary speech both metaphysical and epistemic modalities are often expressed in similar words; the following contrasts may help:A person, Jones, might reasonably say both: (1) "No, it is not possible that Bigfoot
Bigfoot
Bigfoot, also known as sasquatch, is an ape-like cryptid that purportedly inhabits forests, mainly in the Pacific Northwest region of North America. Bigfoot is usually described as a large, hairy, bipedal humanoid...
exists; I am quite certain of that"; and, (2) "Sure, Bigfoot possibly could exist". What Jones means by (1) is that given all the available information, there is no question remaining as to whether Bigfoot exists. This is an epistemic claim. By (2) he makes the metaphysical claim that it is possible for Bigfoot to exist, even though he does not (which is not equivalent to "it is possible that Bigfoot exists – for all I know", which contradicts (1)).
From the other direction, Jones might say, (3) "It is possible that Goldbach's conjecture
Goldbach's conjecture
Goldbach's conjecture is one of the oldest unsolved problems in number theory and in all of mathematics. It states:A Goldbach number is a number that can be expressed as the sum of two odd primes...
is true; but also possible that it is false", and also (4) "if it is true, then it is necessarily true, and not possibly false". Here Jones means that it is epistemically possible that it is true or false, for all he knows (Goldbach's conjecture has not been proven either true or false), but if there is a proof (heretofore undiscovered), then it would show that it is not logically possible for Goldbach's conjecture to be false—there could be no set of numbers that violated it. Logical possibility is a form of alethic possibility; (4) makes a claim about whether it is possible (i.e., logically speaking) that a mathematical truth to have been false, but (3) only makes a claim about whether it is possible, for all Jones knows, (i.e., speaking of certitude) that the mathematical claim is specifically either true or false, and so again Jones does not contradict himself. It is worthwhile to observe that Jones is not necessarily correct: It is possible (epistemically) that Goldbach's conjecture is both true and unprovable.
Epistemic possibilities also bear on the actual world in a way that metaphysical possibilities do not. Metaphysical possibilities bear on ways the world might have been, but epistemic possibilities bear on the way the world may be (for all we know). Suppose, for example, that I want to know whether or not to take an umbrella before I leave. If you tell me "it is possible that it is raining outside" – in the sense of epistemic possibility – then that would weigh on whether or not I take the umbrella. But if you just tell me that "it is possible for it to rain outside" – in the sense of metaphysical possibility – then I am no better off for this bit of modal enlightenment.
Some features of epistemic modal logic are in debate. For example, if x knows that p, does x know that it knows that p? That is to say, should
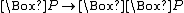 be an axiom in these systems? While the answer to this question is unclear, there is at least one axiom that must be included in epistemic modal logic, because it is minimally true of all modal logics (see the section on axiomatic systems):
be an axiom in these systems? While the answer to this question is unclear, there is at least one axiom that must be included in epistemic modal logic, because it is minimally true of all modal logics (see the section on axiomatic systems):
- K, Distribution Axiom:
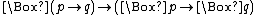 .
.
But this is disconcerting, because with K, we can prove that we know all the logical consequences of our beliefs: If q is a logical consequence of p, then
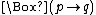 . And if so, then we can deduce that
. And if so, then we can deduce that 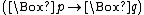 using K. When we translate this into epistemic terms, this says that if q is a logical consequence of p, then we know that it is, and if we know p, we know q. That is to say, we know all the logical consequences of our beliefs. This must be true for all possible Kripkean
using K. When we translate this into epistemic terms, this says that if q is a logical consequence of p, then we know that it is, and if we know p, we know q. That is to say, we know all the logical consequences of our beliefs. This must be true for all possible KripkeanKripke semantics
Kripke semantics is a formal semantics for non-classical logic systems created in the late 1950s and early 1960s by Saul Kripke. It was first made for modal logics, and later adapted to intuitionistic logic and other non-classical systems...
modal interpretations of epistemic cases where
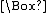 is translated as "knows that". But then, for example, if x knows that prime numbers are divisible only by themselves and the number one, then x knows that 8683317618811886495518194401279999999 is prime (since this number is only divisible by itself and the number one). That is to say, under the modal interpretation of knowledge, anyone who knows the definition of a prime number knows that this number is prime. This shows that epistemic modal logic is an idealized account of knowledge, and explains objective, rather than subjective knowledge (if anything).
is translated as "knows that". But then, for example, if x knows that prime numbers are divisible only by themselves and the number one, then x knows that 8683317618811886495518194401279999999 is prime (since this number is only divisible by itself and the number one). That is to say, under the modal interpretation of knowledge, anyone who knows the definition of a prime number knows that this number is prime. This shows that epistemic modal logic is an idealized account of knowledge, and explains objective, rather than subjective knowledge (if anything).Temporal logic
Temporal logic is an approach to the semantics of expressions with tenseGrammatical tense
A tense is a grammatical category that locates a situation in time, to indicate when the situation takes place.Bernard Comrie, Aspect, 1976:6:...
, that is, expressions with qualifications of when. Some expressions, such as '2 + 2 = 4', are true at all times, while tensed expressions such as 'John is happy' are only true sometimes.
In temporal logic, tense constructions are treated in terms of modalities, where a standard method for formalizing talk of time is to use two pairs of operators, one for the past and one for the future (P will just mean 'it is presently the case that P'). For example:
- FP : It will sometimes be the case that P
- GP : It will always be the case that P
- PP : It was sometime the case that P
- HP : It has always been the case that P
There are then at least three modal logics that we can develop. For example, we can stipulate that,
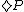 = P is the case at some time t
= P is the case at some time t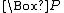 = P is the case at every time t
= P is the case at every time tOr we can trade these operators to deal only with the future (or past). For example,
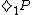 = FP
= FP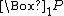 = GP
= GPor,
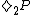 = P and/or FP
= P and/or FP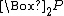 = P and GP
= P and GPThe operators F and G may seem initially foreign, but they create normal modal systems
Normal modal logic
In logic, a normal modal logic is a set L of modal formulas such that L contains:* All propositional tautologies;* All instances of the Kripke schema: \Box\toand it is closed under:...
. Note that FP is the same as ¬G¬P. We can combine the above operators to form complex statements. For example, PP →
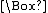 PP says (effectively), Everything that is past and true is necessary.
PP says (effectively), Everything that is past and true is necessary.It seems reasonable to say that possibly it will rain tomorrow, and possibly it won't; on the other hand, seeing as how we can't change the past, if it is true that it rained yesterday, it probably isn't true that it may not have rained yesterday. It seems the past is "fixed", or necessary, in a way the future is not. This is sometimes referred to as accidental necessity
Accidental necessity
In philosophy and logic, accidental necessity, often stated in its Latin form, necessitas per accidens, refers to the necessity attributed to the past by certain views of time...
. But if the past is "fixed", and everything that is in the future will eventually be in the past, then it seems plausible to say that future events are necessary too.
Similarly, the problem of future contingents considers the semantics of assertions about the future: is either of the propositions 'There will be a sea battle tomorrow', or 'There will not be a sea battle tomorrow' now true? Considering this thesis led Aristotle
Aristotle
Aristotle was a Greek philosopher and polymath, a student of Plato and teacher of Alexander the Great. His writings cover many subjects, including physics, metaphysics, poetry, theater, music, logic, rhetoric, linguistics, politics, government, ethics, biology, and zoology...
to reject the principle of bivalence
Principle of bivalence
In logic, the semantic principle of bivalence states that every declarative sentence expressing a proposition has exactly one truth value, either true or false...
for assertions concerning the future.
Additional binary operators are also relevant to temporal logics, q.v. Linear Temporal Logic
Linear temporal logic
In logic, Linear temporal logic is a modal temporal logic with modalities referring to time. In LTL, one can encode formulae about the future of paths such as that a condition will eventually be true, that a condition will be true until another fact becomes true, etc. It is a fragment of the more...
.
Versions of temporal logic can be used in computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
to model computer operations and prove theorems about them. In one version,
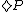 means "at a future time in the computation it is possible that the computer state will be such that P is true";
means "at a future time in the computation it is possible that the computer state will be such that P is true"; 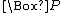 means "at all future times in the computation P will be true". In another version,
means "at all future times in the computation P will be true". In another version, 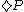 means "at the immediate next state of the computation, P might be true";
means "at the immediate next state of the computation, P might be true"; 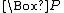 means "at the immediate next state of the computation, P will be true". These differ in the choice of Accessibility relation
means "at the immediate next state of the computation, P will be true". These differ in the choice of Accessibility relationAccessibility relation
In modal logic, an accessibility relation is a binary relation, written as R\,\! between possible worlds.-Description of terms:A statement in logic refers to a sentence that can be true or false...
. (P always means "P is true at the current computer state".) These two examples involve nondeterministic or not-fully-understood computations; there are many other modal logics specialized to different types of program analysis. Each one naturally leads to slightly different axioms.
A variation, closely related to Temporal or Chronological or Tense logics, are Modal logics based upon "topology", "place", or "spatial position". One might also take note that in the Russian language, verbs have an aspect, based commonly upon time, but position also.
Deontic logic
Likewise talk of morality, or of obligationObligation
An obligation is a requirement to take some course of action, whether legal or moral. There are also obligations in other normative contexts, such as obligations of etiquette, social obligations, and possibly...
and norms
Norm (philosophy)
Norms are concepts of practical import, oriented to effecting an action, rather than conceptual abstractions that describe, explain, and express. Normative sentences imply “ought-to” types of statements and assertions, in distinction to sentences that provide “is” types of statements and assertions...
generally, seems to have a modal structure. The difference between "You must do this" and "You may do this" looks a lot like the difference between "This is necessary" and "This is possible". Such logics are called deontic
Deontic logic
Deontic logic is the field of logic that is concerned with obligation, permission, and related concepts. Alternatively, a deontic logic is a formal system that attempts to capture the essential logical features of these concepts...
, from the Greek for "duty".
Deontic logics commonly lack the axiom T semantically corresponding to the reflexivity of the accessibility relation in Kripke semantics
Kripke semantics
Kripke semantics is a formal semantics for non-classical logic systems created in the late 1950s and early 1960s by Saul Kripke. It was first made for modal logics, and later adapted to intuitionistic logic and other non-classical systems...
: in symbols,
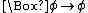 . Interpreting
. Interpreting 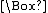 as "it is obligatory that", T informally says that every obligation is true. For example, if it is obligatory not to kill others (i.e. killing is morally forbidden), then T implies that people actually do not kill others. The consequent is obviously false.
as "it is obligatory that", T informally says that every obligation is true. For example, if it is obligatory not to kill others (i.e. killing is morally forbidden), then T implies that people actually do not kill others. The consequent is obviously false.Instead, using Kripke semantics
Kripke semantics
Kripke semantics is a formal semantics for non-classical logic systems created in the late 1950s and early 1960s by Saul Kripke. It was first made for modal logics, and later adapted to intuitionistic logic and other non-classical systems...
, we say that though our own world does not realize all obligations, the worlds accessible to it do (i.e., T holds at these worlds). These worlds are called idealized worlds. P is obligatory with respect to our own world if at all idealized worlds accessible to our world, P holds. Though this was one of the first interpretations of the formal semantics, it has recently come under criticism.
One other principle that is often (at least traditionally) accepted as a deontic principle is D,
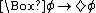 , which corresponds to the seriality (or extendability or unboundedness) of the accessibility relation. It is an embodiment of the Kantian idea that "ought implies can". (Clearly the "can" can be interpreted in various senses, e.g. in a moral or alethic sense.)
, which corresponds to the seriality (or extendability or unboundedness) of the accessibility relation. It is an embodiment of the Kantian idea that "ought implies can". (Clearly the "can" can be interpreted in various senses, e.g. in a moral or alethic sense.)Intuitive problems with deontic logic
When we try and formalize ethics with standard modal logic, we run into some problems. Suppose that we have a proposition K: you have killed the victim, and another, Q: you have killed the victim quickly. Now suppose we want to express the thought that "if you have killed the victim, it ought to be the case that you have killed him quickly". There are two likely candidates,- (1)
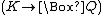
- (2)
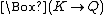
But (1) says that if you have killed the victim, then it ought to be the case that you have killed him quickly. This surely isn't right, because you ought not to have killed him at all. And (2) doesn't work either. If the right representation of "if you have killed the victim then you ought to have killed him quickly" is (2), then the right representation of (3) "if you have killed the victim then you ought to have killed him slowly" is
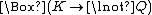 . Now suppose (as seems reasonable) that you should not have killed the victim, or
. Now suppose (as seems reasonable) that you should not have killed the victim, or 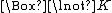 . But then we can deduce
. But then we can deduce 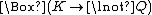 , which would express sentence (3). So if you should not have killed the victim, then if you did kill him, you should have killed him slowly. But that can't be right, and is not right when we use natural language. Telling someone they should not kill the victim certainly does not imply that they should kill the victim slowly if they do kill him.
, which would express sentence (3). So if you should not have killed the victim, then if you did kill him, you should have killed him slowly. But that can't be right, and is not right when we use natural language. Telling someone they should not kill the victim certainly does not imply that they should kill the victim slowly if they do kill him.Doxastic logic
Doxastic logic concerns the logic of belief (of some set of agents). The term doxastic is derived from the ancient GreekAncient Greek
Ancient Greek is the stage of the Greek language in the periods spanning the times c. 9th–6th centuries BC, , c. 5th–4th centuries BC , and the c. 3rd century BC – 6th century AD of ancient Greece and the ancient world; being predated in the 2nd millennium BC by Mycenaean Greek...
doxa which means "belief". Typically, a doxastic logic uses
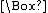 , often written "B", to mean "It is believed that", or when relativized to a particular agent s, "It is believed by s that".
, often written "B", to mean "It is believed that", or when relativized to a particular agent s, "It is believed by s that".Other modal logics
Significantly, modal logics can be developed to accommodate most of these idioms; it is the fact of their common logical structure (the use of "intensional" sentential operators) that make them all varieties of the same thing.The ontology of possibility
In the most common interpretation of modal logic, one considers "logically possible worlds". If a statement is true in all possible worldsPossible Worlds
Possible Worlds may refer to:* Possible worlds, a concept in philosophy* Possible Worlds , by John Mighton** Possible Worlds , by Robert Lepage, based on the Mighton play* Possible Worlds , by Peter Porter...
, then it is a necessary truth. If a statement happens to be true in our world, but is not true in all possible worlds, then it is a contingent truth. A statement that is true in some possible world (not necessarily our own) is called a possible truth.
Under this "possible worlds idiom," to maintain that Bigfoot's existence is possible but not actual, one says, "There is some possible world in which Bigfoot exists; but in the actual world, Bigfoot does not exist". However, it is unclear what this claim commits us to. Are we really alleging the existence of possible worlds, every bit as real as our actual world, just not actual? Saul Kripke
Saul Kripke
Saul Aaron Kripke is an American philosopher and logician. He is a professor emeritus at Princeton and teaches as a Distinguished Professor of Philosophy at the CUNY Graduate Center...
believes that 'possible world' is something of a misnomer – that the term 'possible world' is just a useful way of visualizing the concept of possibility. For him, the sentences "you could have rolled a 4 instead of a 6" and "there is a possible world where you rolled a 4, but you rolled a 6 in the actual world" are not significantly different statements, and neither commit us to the existence of a possible world. David Lewis, on the other hand, made himself notorious by biting the bullet, asserting that all merely possible worlds are as real as our own, and that what distinguishes our world as actual is simply that it is indeed our world – this
Indexicality
In linguistics and in philosophy of language, an indexical behavior or utterance points to some state of affairs. For example, I refers to whoever is speaking; now refers to the time at which that word is uttered; and here refers to the place of utterance...
world. That position is a major tenet of "modal realism
Modal realism
Modal realism is the view, notably propounded by David Kellogg Lewis, that all possible worlds are as real as the actual world. It is based on the following tenets: possible worlds exist; possible worlds are not different in kind from the actual world; possible worlds are irreducible entities; the...
". Some philosophers decline to endorse any version of modal realism, considering it ontologically extravagant, and prefer to seek various ways to paraphrase away these ontological commitments. Robert Adams holds that 'possible worlds' are better thought of as 'world-stories', or consistent sets of propositions. Thus, it is possible that you rolled a 4 if such a state of affairs can be described coherently.
Computer scientists will generally pick a highly specific interpretation of the modal operators specialized to the particular sort of computation being analysed. In place of "all worlds", you may have "all possible next states of the computer", or "all possible future states of the computer".
Applications
- Modality has also been treated from the viewpoint of "counter-factuals" in literature (see Victorian StudiesVictorian StudiesVictorian Studies is a peer-reviewed academic journal, published quarterly by Indiana University Press. It covers research on nineteenth-century Britain during the reign of Queen Victoria and publishes essays, forums, and reviews on a variety of topics concerning Victorianism, including...
).
- Modality modifies propositions and modalities provide closure (i.e.: propositions with modalities are still propositions). Thus, as propositions constitute a part of language, they may be understood as subject to linguistic analysis such as that of Noam ChomskyNoam ChomskyAvram Noam Chomsky is an American linguist, philosopher, cognitive scientist, and activist. He is an Institute Professor and Professor in the Department of Linguistics & Philosophy at MIT, where he has worked for over 50 years. Chomsky has been described as the "father of modern linguistics" and...
. Modalities might then be viewed as being context-free, context-sensitive, or even fully phrase-structured (Chomsky type-0) languages. This broadens the view of modalities which are usually viewed as context-free. A discussion of this may be found under the Philosophy of languagePhilosophy of languagePhilosophy of language is the reasoned inquiry into the nature, origins, and usage of language. As a topic, the philosophy of language for analytic philosophers is concerned with four central problems: the nature of meaning, language use, language cognition, and the relationship between language...
.
As an example, consider the following context-sensitive grammar for an alethic Modal logic grammar:
L=({S, X, R, M}, {Φ,
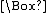 ,
,  , , &,
, , &,  , &, v, ~}, P, S), where Φ is a meta-variable for propositions, and P are the following production rules:
, &, v, ~}, P, S), where Φ is a meta-variable for propositions, and P are the following production rules:S
 XR | M
XR | MXR
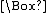 M |
M |  M
MM
 T M | T
T M | TT
 (T
(T  T) | (T & T) | (T v T) | (~T) | Φ
T) | (T & T) | (T v T) | (~T) | ΦA sample derivation:
S
 XR
XR 
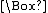 M
M 
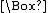 T
T 
 ( T & T )
( T & T ) 
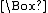 ( Φ & T )
( Φ & T ) 
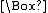 ( p & T )
( p & T ) 
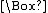 ( p & Φ )
( p & Φ ) 
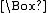 ( p & q )
( p & q )Of course, an equivalent context-free language is easy to construct, but the point here is that a Modal logic based upon a context-sensitive grammar is possible. More complex Modal logics which are Chomsky type-0 or type-1 extends the philosophical discussion of Modal logics.
- Aristotle classified and discussed rhetoricRhetoricRhetoric is the art of discourse, an art that aims to improve the facility of speakers or writers who attempt to inform, persuade, or motivate particular audiences in specific situations. As a subject of formal study and a productive civic practice, rhetoric has played a central role in the Western...
as being based upon the enthymemeEnthymemeAn enthymeme , in its modern sense, is an informally stated syllogism with an unstated assumption that must be true for the premises to lead to the conclusion. In an enthymeme, part of the argument is missing because it is assumed...
, thus closely related to logic. However, it is clear that if logic is extended by modal logics, multi-valued logics, etc., then rhetoric must also be extended by modern developments.
Thus, for example, the following might be persuasive rhetorically:
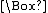 (p & q)
(p & q)______________________________
Therefore
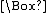 p
pbut ~[
 (p & q)
(p & q)  (
(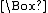 p &
p & 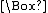 q) ]
q) ]Further applications
Modal logics have begun to be used in area of the humanities such as literature, poetry, art and history.Controversies
Modal logic has been rejected by many philosophers. (Historically, philosophers starting with Aristotle seem to have had priority of interest in modal logic over mathematicians.) The primary reason for this rejection is that modality provides a different logical framework with which to analyze society. Nicholas RescherNicholas Rescher
Nicholas Rescher is an American philosopher at the University of Pittsburgh. In a productive research career extending over six decades, Rescher has established himself as a systematic philosopher of the old style and author of a system of pragmatic idealism which weaves together threads of...
has pointed out how radically conservative were the views of Bertrand Russell
Bertrand Russell
Bertrand Arthur William Russell, 3rd Earl Russell, OM, FRS was a British philosopher, logician, mathematician, historian, and social critic. At various points in his life he considered himself a liberal, a socialist, and a pacifist, but he also admitted that he had never been any of these things...
in his unreasoned rejection of both Modal Logic and the ideas of the philosopher Alexius Meinong
Alexius Meinong
Alexius Meinong was an Austrian philosopher, a realist known for his unique ontology...
. Indeed, Arthur Norman Prior warned his protégé Ruth Barcan to prepare well in the debates concerning Modal Logic (with Willard Van Orman Quine
Willard Van Orman Quine
Willard Van Orman Quine was an American philosopher and logician in the analytic tradition...
) due to the biases against Modal Logic.
See also
- Accessibility relationAccessibility relationIn modal logic, an accessibility relation is a binary relation, written as R\,\! between possible worlds.-Description of terms:A statement in logic refers to a sentence that can be true or false...
- Counterpart theoryCounterpart theoryIn philosophy, specifically in the area of modal metaphysics, counterpart theory is an alternative to standard possible-worlds semantics for interpreting quantified modal logic. Counterpart theory still presupposes possible worlds, but differs in certain important respects from the Kripkean view...
- David Kellogg LewisDavid Kellogg LewisDavid Kellogg Lewis was an American philosopher. Lewis taught briefly at UCLA and then at Princeton from 1970 until his death. He is also closely associated with Australia, whose philosophical community he visited almost annually for more than thirty years...
- De dicto and de reDe dicto and de reDe dicto and de re are two phrases used to mark important distinctions in intensional statements, associated with the intensional operators in many such statements. The distinctions are most recognized in philosophy of language and metaphysics....
- Description logicDescription logicDescription logic is a family of formal knowledge representation languages. It is more expressive than propositional logic but has more efficient decision problems than first-order predicate logic....
- Doxastic logic
- Dynamic logicDynamic logic (modal logic)Dynamic logic is an extension of modal logic originally intended for reasoning about computer programs and later applied to more general complex behaviors arising in linguistics, philosophy, AI, and other fields.-Language:...
- Epistemic logicEpistemic logicEpistemic modal logic is a subfield of modal logic that is concerned with reasoning about knowledge. While epistemology has a long philosophical tradition dating back to Ancient Greece, epistemic logic is a much more recent development with applications in many fields, including philosophy,...
- EnthymemeEnthymemeAn enthymeme , in its modern sense, is an informally stated syllogism with an unstated assumption that must be true for the premises to lead to the conclusion. In an enthymeme, part of the argument is missing because it is assumed...
- Hybrid logicHybrid logicHybrid logic refers to a number of extensions to propositional modal logic with more expressive power, though still less than first-order logic. In formal logic, there is a trade-off between expressiveness and computational tractability . The history of hybrid logic began with Arthur Prior's work...
- Interior algebraInterior algebraIn abstract algebra, an interior algebra is a certain type of algebraic structure that encodes the idea of the topological interior of a set. Interior algebras are to topology and the modal logic S4 what Boolean algebras are to set theory and ordinary propositional logic...
- Interpretability logicInterpretability logicInterpretability logics comprise a family of modal logics that extend provability logic to describe interpretability and/or various related metamathematical properties and relations such as weak interpretability, Π1-conservativity, cointerpretability, tolerance, cotolerance and arithmetic...
- Kripke semanticsKripke semanticsKripke semantics is a formal semantics for non-classical logic systems created in the late 1950s and early 1960s by Saul Kripke. It was first made for modal logics, and later adapted to intuitionistic logic and other non-classical systems...
- Multi-valued logicMulti-valued logicIn logic, a many-valued logic is a propositional calculus in which there are more than two truth values. Traditionally, in Aristotle's logical calculus, there were only two possible values for any proposition...
- Possible worldsPossible WorldsPossible Worlds may refer to:* Possible worlds, a concept in philosophy* Possible Worlds , by John Mighton** Possible Worlds , by Robert Lepage, based on the Mighton play* Possible Worlds , by Peter Porter...
- Provability logicProvability logicProvability logic is a modal logic, in which the box operator is interpreted as 'it is provable that'. The point is to capture the notion of a proof predicate of a reasonably rich formal theory, such as Peano arithmetic....
- Regular modal logicRegular modal logicIn modal logic, a regular modal logic L is a modal logic closed under the duality of the modal operators:\Diamond A \equiv \lnot\Box\lnot Aand the rule\to C \vdash \to\Box C....
- Research Materials: Max Planck Society ArchiveResearch Materials: Max Planck Society ArchiveAt the end of World War II, the Kaiser Wilhelm Society was renamed the Max Planck Society, and the institutes associated with the Kaiser Wilhelm Society were renamed "Max Planck" institutes. The records that were archived under the former Kaiser Wilhelm Society and its institutes were placed in the...
- RhetoricRhetoricRhetoric is the art of discourse, an art that aims to improve the facility of speakers or writers who attempt to inform, persuade, or motivate particular audiences in specific situations. As a subject of formal study and a productive civic practice, rhetoric has played a central role in the Western...
- Two dimensionalismTwo dimensionalismTwo-dimensionalism is an approach to semantics in analytic philosophy. It is a theory of how to determine the sense and reference of a word and the truth-value of a sentence...
- Modal verbModal verbA modal verb is a type of auxiliary verb that is used to indicate modality -- that is, likelihood, ability, permission, and obligation...
Further reading
- D.M. Gabbay, A. Kurucz, F. Wolter and M. Zakharyaschev, Many-Dimensional Modal Logics: Theory and Applications, Elsevier, Studies in Logic and the Foundations of Mathematics, volume 148, 2003, ISBN 0-444-50826-0. Covers many varieties of modal logics, e.g. temporal, epistemic, dynamic, description, spatial from a unified perspective with emphasis on computer science aspects, e.g. decidability and complexity.
External links
- Stanford Encyclopedia of PhilosophyStanford Encyclopedia of PhilosophyThe Stanford Encyclopedia of Philosophy is a freely-accessible online encyclopedia of philosophy maintained by Stanford University. Each entry is written and maintained by an expert in the field, including professors from over 65 academic institutions worldwide...
:- "Modal logic" – by James GarsonJames GarsonJames Garson is an American philosopher and logician. He has made significant contributions in the study of modal logic and formal semantics, and is author of Modal Logic for Philosophers by Cambridge University Press...
. - "Provability Logic" – by Rineke Verbrugge.
- "Modal logic" – by James Garson
- Edward N. ZaltaEdward N. ZaltaEdward N. Zalta is a Senior research scholar at the Center for the Study of Language and Information. He received his Ph.D. in philosophy from the University of Massachusetts - Amherst in 1980. Zalta has taught courses at Stanford University, Rice University, the University of Salzburg, and the...
, 1995, "Basic Concepts in Modal Logic." - John McCarthyJohn McCarthy (computer scientist)John McCarthy was an American computer scientist and cognitive scientist. He coined the term "artificial intelligence" , invented the Lisp programming language and was highly influential in the early development of AI.McCarthy also influenced other areas of computing such as time sharing systems...
, 1996, "Modal Logic." - Molle a Java prover for experimenting with modal logics
- Suber, Peter, 2002, "Bibliography of Modal Logic."
- Marcus, Ruth Barcan, "Modalities" OUP 1993, 1995
- List of Logic Systems List of many modal logics with sources, by John Halleck.
- Advances in Modal Logic. Biannual international conference and book series in modal logic.
- S4prover A tableaux prover for S4 logic

