Standard part function
Encyclopedia
In non-standard analysis
, the standard part function is a function from the limited (finite) hyperreals to the reals, which associates to every hyperreal, the unique real infinitely close to it. As such, it is a mathematical implementation of the historical concept of adequality
introduced by Pierre de Fermat
. The standard part function was first defined by Abraham Robinson
as a key ingredient in defining the concepts of the calculus, such as the derivative and the integral, in non-standard analysis
. The latter theory is a rigorous formalisation of calculations with infinitesimal
s.
line. The latter is an extension of the real line which contains, in addition to the reals, also infinitely small quantities. In the hyperreal line every real number has a collection of numbers (called a monad) of hyperreals infinitely close to it. The standard part function associates to a finite hyperreal
x, the unique standard real number x0 which infinitely close to it. The relationship is expressed symbolically by writing
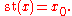
The standard part of any infinitesimal
is 0. Thus if N is an infinite hypernatural, then 1/N is infinitesimal, and st(1/N) = 0.
. There are several ways of explaining this. Perhaps the simplest is that its domain L, which is the collection of limited (i.e. finite) hyperreals, is not an internal set. Namely, since L is bounded (by any infinite hypernatural, for instance), L would have to have a least upper bound if L were internal, but L doesn't have a least upper bound. Alternatively, the range of "st" is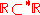
which is not internal; in fact every internal subset of 
is necessarily finite, see (Goldblatt, 1998).
Non-standard analysis
Non-standard analysis is a branch of mathematics that formulates analysis using a rigorous notion of an infinitesimal number.Non-standard analysis was introduced in the early 1960s by the mathematician Abraham Robinson. He wrote:...
, the standard part function is a function from the limited (finite) hyperreals to the reals, which associates to every hyperreal, the unique real infinitely close to it. As such, it is a mathematical implementation of the historical concept of adequality
Adequality
In the history of infinitesimal calculus, adequality is a technique developed by Pierre de Fermat. Fermat said he borrowed the term from Diophantus. Adequality was a technique first used to find maxima for functions and then adapted to find tangent lines to curves...
introduced by Pierre de Fermat
Pierre de Fermat
Pierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...
. The standard part function was first defined by Abraham Robinson
Abraham Robinson
Abraham Robinson was a mathematician who is most widely known for development of non-standard analysis, a mathematically rigorous system whereby infinitesimal and infinite numbers were incorporated into mathematics....
as a key ingredient in defining the concepts of the calculus, such as the derivative and the integral, in non-standard analysis
Non-standard analysis
Non-standard analysis is a branch of mathematics that formulates analysis using a rigorous notion of an infinitesimal number.Non-standard analysis was introduced in the early 1960s by the mathematician Abraham Robinson. He wrote:...
. The latter theory is a rigorous formalisation of calculations with infinitesimal
Infinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
s.
Definition
Nonstandard analysis deals primarily with the hyperrealHyperreal number
The system of hyperreal numbers represents a rigorous method of treating the infinite and infinitesimal quantities. The hyperreals, or nonstandard reals, *R, are an extension of the real numbers R that contains numbers greater than anything of the form1 + 1 + \cdots + 1. \, Such a number is...
line. The latter is an extension of the real line which contains, in addition to the reals, also infinitely small quantities. In the hyperreal line every real number has a collection of numbers (called a monad) of hyperreals infinitely close to it. The standard part function associates to a finite hyperreal
Hyperreal number
The system of hyperreal numbers represents a rigorous method of treating the infinite and infinitesimal quantities. The hyperreals, or nonstandard reals, *R, are an extension of the real numbers R that contains numbers greater than anything of the form1 + 1 + \cdots + 1. \, Such a number is...
x, the unique standard real number x0 which infinitely close to it. The relationship is expressed symbolically by writing
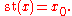
The standard part of any infinitesimal
Infinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
is 0. Thus if N is an infinite hypernatural, then 1/N is infinitesimal, and st(1/N) = 0.
Not internal
The standard part function "st" is not defined by an internal setInternal set
In mathematical logic, in particular in model theory and non-standard analysis, an internal set is a set that is a member of a model.Internal set is the key tool in formulating the transfer principle, which concerns the logical relation between the properties of the real numbers R, and the...
. There are several ways of explaining this. Perhaps the simplest is that its domain L, which is the collection of limited (i.e. finite) hyperreals, is not an internal set. Namely, since L is bounded (by any infinite hypernatural, for instance), L would have to have a least upper bound if L were internal, but L doesn't have a least upper bound. Alternatively, the range of "st" is
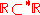which is not internal; in fact every internal subset of is necessarily finite, see (Goldblatt, 1998).