
Equation of time
Encyclopedia
Astronomical Almanac
The Astronomical Almanac is an almanac published by the United States Naval Observatory and Her Majesty's Nautical Almanac Office, containing solar system ephemeris and catalogs of selected stellar and extragalactic objects....
) or estimated with formulas given below.
Apparent (or true) solar time can be obtained for example by measurement of the current position (hour angle) of the Sun, or indicated (with limited accuracy) by a sundial
Sundial
A sundial is a device that measures time by the position of the Sun. In common designs such as the horizontal sundial, the sun casts a shadow from its style onto a surface marked with lines indicating the hours of the day. The style is the time-telling edge of the gnomon, often a thin rod or a...
. Mean solar time, for the same place, would be the time indicated by a steady clock set so that over the year its differences from apparent solar time average to zero (with zero net gain or loss over the year).
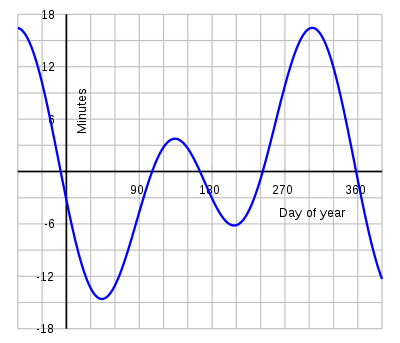
During a year the equation of time varies as shown on the graph; its change from one year to the next is slight. Apparent time, and the sundial, can be ahead (fast) by as much as 16 min
Minute
A minute is a unit of measurement of time or of angle. The minute is a unit of time equal to 1/60th of an hour or 60 seconds. In the UTC time scale, a minute on rare occasions has 59 or 61 seconds; see leap second. The minute is not an SI unit; however, it is accepted for use with SI units...
33 s
Second
The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....
(around 3 November), or behind (slow) by as much as 14 min 6 s (around 12 February). The equation of time has zeros near 15 April, 13 June, 1 September and 25 December.
The graph of the equation of time is closely approximated by the sum of two sine curves, one with a period of a year and one with a period of half a year. The curves reflect two astronomical effects, each causing a different non-uniformity in the apparent daily motion of the Sun relative to the stars:
- the obliquity of the eclipticEclipticThe ecliptic is the plane of the earth's orbit around the sun. In more accurate terms, it is the intersection of the celestial sphere with the ecliptic plane, which is the geometric plane containing the mean orbit of the Earth around the Sun...
(the plane of the Earth's annual orbital motion around the Sun), which is inclined by about 23.44 degrees relative to the plane of the Earth's equatorEquatorAn equator is the intersection of a sphere's surface with the plane perpendicular to the sphere's axis of rotation and containing the sphere's center of mass....
; and
- the eccentricity of the Earth's orbitEarth's orbitIn astronomy, the Earth's orbit is the motion of the Earth around the Sun, at an average distance of about 150 million kilometers, every 365.256363 mean solar days .A solar day is on average 24 hours; it takes 365.256363 of these to orbit the sun once in the sense of returning...
around the Sun, which is about 0.017.
The equation of time is also the east or west component of the analemma
Analemma
In astronomy, an analemma is a curve representing the angular offset of a celestial body from its mean position on the celestial sphere as viewed from another celestial body relative to the viewing body's celestial equator...
, a curve representing the angular offset of the Sun from its mean position on the celestial sphere as viewed from Earth.
The equation of time was used historically to set clocks. Between the invention of accurate clocks in 1656 and the advent of commercial time distribution services around 1900, one of two common land-based ways to set clocks was by observing the passage of the sun across the local meridian
Meridian (astronomy)
This article is about the astronomical concept. For other uses of the word, see Meridian.In the sky, a meridian is an imaginary great circle on the celestial sphere. It passes through the north point on the horizon, through the celestial pole, up to the zenith, through the south point on the...
at noon. The moment the sun passed overhead, the clock was set to noon, offset by the number of minutes given by the equation of time for that date. (The second method did not use the equation of time; instead, it used stellar observations to give sidereal time
Sidereal time
Sidereal time is a time-keeping system astronomers use to keep track of the direction to point their telescopes to view a given star in the night sky...
, in combination with the relation between sidereal time and solar time
Solar time
Solar time is a reckoning of the passage of time based on the Sun's position in the sky. The fundamental unit of solar time is the day. Two types of solar time are apparent solar time and mean solar time .-Introduction:...
.) The equation of time values for each day of the year, compiled by astronomical observatories
Observatory
An observatory is a location used for observing terrestrial or celestial events. Astronomy, climatology/meteorology, geology, oceanography and volcanology are examples of disciplines for which observatories have been constructed...
, were widely listed in almanac
Almanac
An almanac is an annual publication that includes information such as weather forecasts, farmers' planting dates, and tide tables, containing tabular information in a particular field or fields often arranged according to the calendar etc...
s and ephemerides
Ephemeris
An ephemeris is a table of values that gives the positions of astronomical objects in the sky at a given time or times. Different kinds of ephemerides are used for astronomy and astrology...
.
Naturally, other planet
Planet
A planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
s will have an equation of time too. On Mars
Mars
Mars is the fourth planet from the Sun in the Solar System. The planet is named after the Roman god of war, Mars. It is often described as the "Red Planet", as the iron oxide prevalent on its surface gives it a reddish appearance...
the difference between sundial time and clock time can be as much as 50 minutes, due to the considerably greater eccentricity of its orbit. The planet Uranus
Uranus
Uranus is the seventh planet from the Sun. It has the third-largest planetary radius and fourth-largest planetary mass in the Solar System. It is named after the ancient Greek deity of the sky Uranus , the father of Cronus and grandfather of Zeus...
, which has an extremely large axial tilt, has an equation of time that can be several hours.
Ancient history — Babylon and Egypt
The irregular daily movement of the Sun was known by the Babylonians, and Book III of Ptolemy'sPtolemy
Claudius Ptolemy , was a Roman citizen of Egypt who wrote in Greek. He was a mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in Egypt under Roman rule, and is believed to have been born in the town of Ptolemais Hermiou in the...
Almagest
Almagest
The Almagest is a 2nd-century mathematical and astronomical treatise on the apparent motions of the stars and planetary paths. Written in Greek by Claudius Ptolemy, a Roman era scholar of Egypt,...
is primarily concerned with the Sun's anomaly. Ptolemy discusses the correction needed to convert the meridian crossing of the Sun to mean solar time and takes into consideration the nonuniform motion of the Sun along the ecliptic and the meridian correction for the Sun's ecliptic longitude. He states the maximum correction is 8 1/3 time-degrees or 5/9 of an hour (Book III, chapter 9). However he did not consider the effect relevant for most calculations since it was negligible for the slow-moving luminaries and only applied it for the fastest-moving luminary, the Moon.
Medieval and Renaissance astronomy
Toomer uses the Medieval term equation, from the Latin term aequatio (equalizationApparent time versus mean time
Until the invention of the pendulum and the development of reliable clocks during the 17th century, the equation of time as defined by Ptolemy remained a curiosity, of importance only to astronomers. However, when mechanical clocks started to take over timekeeping from sundials, which had served humanity for centuries, the difference between clock time and solar time became an issue for everyday life. Apparent solar time (or true or real solar time) is the time indicated by the Sun on a sundial (or measured by its transit over the local meridian), while mean solar time is the average as indicated by well-regulated clocks. The first tables for the equation of time which accounted for its annual variations in an essentially correct way were published in 1665 by Christiaan Huygens. Huygens set his values for the equation of time so as to make all values positive throughout the year. This meant that a clock set by Huygens' tables would be consistently about 15 minutes slow on mean time.Another set of tables was published in 1672/73 by John Flamsteed
John Flamsteed
Sir John Flamsteed FRS was an English astronomer and the first Astronomer Royal. He catalogued over 3000 stars.- Life :Flamsteed was born in Denby, Derbyshire, England, the only son of Stephen Flamsteed...
, who later became the first royal astronomer of the new Greenwich Observatory. These appear to have been the first essentially correct tables which also led to mean time without an offset. Flamsteed adopted the convention of tabulating and naming the correction in the sense that it was to be applied to the apparent time to give mean time.
The equation of time, correctly based on the two major components of the Sun's
irregularity of apparent motion, i.e. the effect of the obliquity of the ecliptic and the effect of the Earth's orbital eccentricity, was not generally adopted until after Flamsteed's tables of 1672/3, published with the posthumous edition of the works of Jeremiah Horrocks.
Robert Hooke
Robert Hooke
Robert Hooke FRS was an English natural philosopher, architect and polymath.His adult life comprised three distinct periods: as a scientific inquirer lacking money; achieving great wealth and standing through his reputation for hard work and scrupulous honesty following the great fire of 1666, but...
(1635-1703), who mathematically analyzed the universal joint
Universal joint
A universal joint, universal coupling, U joint, Cardan joint, Hardy-Spicer joint, or Hooke's joint is a joint or coupling in a rigid rod that allows the rod to 'bend' in any direction, and is commonly used in shafts that transmit rotary motion...
, was the first to note that the geometry and mathematical description of the (non-secular) equation of time and the universal joint were identical, and proposed the use of a universal joint in the construction of a "mechanical sundial".
Eighteenth and early nineteenth centuries
The corrections in Flamsteed's tables of 1672/3 and 1680 led to mean time computed essentially correctly and without an offset, i.e. in principle as we now know it. But the numerical values in tables of the equation of time have somewhat changed since then, owing to three kinds of factors:- general improvements in accuracy that came from refinements in astronomical measurement techniques,
- slow intrinsic changes in the equation of time, occurring as a result of very slow long-term changes in the Earth's obliquity and eccentricity and the position of its perihelion (or, equivalently, of the Sun's perigee), and
- the inclusion of small sources of additional variation in the apparent motion of the Sun, unknown in the 17th century, but discovered from the eighteenth century onwards, including the effects of the Moon, Venus and Jupiter.
Until 1833, the equation of time was tabulated in the sense 'mean minus apparent solar time' in the British Nautical Almanac and Astronomical Ephemeris
Nautical Almanac
Nautical Almanac can refer to:* Nautical almanac - a publication describing the positions and movements of celestial bodies* American Ephemeris and Nautical Almanac - first published in 1852* U.S...
published for the years 1767 onwards. Before the issue for 1834, all times in the almanac were in apparent solar time, because time aboard ship was most often determined by observing the Sun. In the unusual case that the mean solar time of an observation was needed, the extra step of adding the equation of time to apparent solar time was needed. In the Nautical Almanac issues for 1834 onwards, all times have been in mean solar time, because by then the time aboard ship was increasingly often determined by marine chronometer
Marine chronometer
A marine chronometer is a clock that is precise and accurate enough to be used as a portable time standard; it can therefore be used to determine longitude by means of celestial navigation...
s. In the unusual case that the apparent solar time of an observation was needed, the extra step of applying the equation of time to mean solar time was needed, requiring all differences in the equation of time to have the opposite sign than before.
As the apparent daily movement of the Sun is one revolution per day, that is 360° every 24 hours, and the Sun itself appears as a disc of about 0.5° in the sky, simple sundials can be read to a maximum accuracy of about one minute. Since the equation of time has a range of about 30 minutes, the difference between sundial time and clock time cannot be ignored. In addition to the equation of time, one also has to apply corrections due to one's distance from the local time zone meridian and summer time
Daylight saving time
Daylight saving time —also summer time in several countries including in British English and European official terminology —is the practice of temporarily advancing clocks during the summertime so that afternoons have more daylight and mornings have less...
, if any.
The tiny increase of the mean solar day itself due to the slowing down of the Earth's rotation, by about 2 ms per day per century, which currently accumulates up to about 1 second every year, is not taken into account in traditional definitions of the equation of time, as it is imperceptible at the accuracy level of sundials.
Eccentricity of the Earth's orbit
The Earth revolves around the Sun. As seen from Earth, the Sun appears to revolve once around the Earth through the background stars in one year. If the Earth orbited the Sun with a constant speed, in a circular orbit in a plane perpendicular to the Earth's axis, then the Sun would culminateCulmination
In astronomy, the culmination of a planet, star, constellation, etc. is the altitude reached when the object transits over an observer's meridian....
every day at exactly the same time, and be a perfect time keeper (except for the very small effect of the slowing rotation of the Earth). But the orbit of the Earth is an ellipse, and its speed varies between 30.287 and 29.291 km/s, according to Kepler's laws of planetary motion
Kepler's laws of planetary motion
In astronomy, Kepler's laws give a description of the motion of planets around the Sun.Kepler's laws are:#The orbit of every planet is an ellipse with the Sun at one of the two foci....
, and its angular speed also varies, and thus the Sun appears to move faster (relative to the background stars) at perihelion (currently around January 3) and slower at aphelion a half year later. At these extreme points, this effect increases (respectively, decreases) the real solar day by 7.9 seconds from its mean. This daily difference accumulates over a period. As a result, the eccentricity of the Earth's orbit contributes a sine wave variation with an amplitude of 7.66 minutes and a period of one year to the equation of time. The zero points are reached at perihelion (at the beginning of January) and aphelion (beginning of July) while the maximum values are in early April (negative) and early October (positive).
Obliquity of the ecliptic

Celestial equator
The celestial equator is a great circle on the imaginary celestial sphere, in the same plane as the Earth's equator. In other words, it is a projection of the terrestrial equator out into space...
would still not be uniform. This is a consequence of the tilt of the Earth's rotation with respect to its orbit, or equivalently, the tilt of the ecliptic
Ecliptic
The ecliptic is the plane of the earth's orbit around the sun. In more accurate terms, it is the intersection of the celestial sphere with the ecliptic plane, which is the geometric plane containing the mean orbit of the Earth around the Sun...
(the path of the sun against the celestial sphere
Celestial sphere
In astronomy and navigation, the celestial sphere is an imaginary sphere of arbitrarily large radius, concentric with the Earth and rotating upon the same axis. All objects in the sky can be thought of as projected upon the celestial sphere. Projected upward from Earth's equator and poles are the...
) with respect to the celestial equator
Celestial equator
The celestial equator is a great circle on the imaginary celestial sphere, in the same plane as the Earth's equator. In other words, it is a projection of the terrestrial equator out into space...
. The projection of this motion onto the celestial equator
Celestial equator
The celestial equator is a great circle on the imaginary celestial sphere, in the same plane as the Earth's equator. In other words, it is a projection of the terrestrial equator out into space...
, along which "clock time" is measured, is a maximum at the solstices, when the yearly movement of the Sun is parallel to the equator and appears as a change in right ascension
Right ascension
Right ascension is the astronomical term for one of the two coordinates of a point on the celestial sphere when using the equatorial coordinate system. The other coordinate is the declination.-Explanation:...
, and is a minimum at the equinoxes, when the Sun moves in a sloping direction and appears mainly as a change in declination
Declination
In astronomy, declination is one of the two coordinates of the equatorial coordinate system, the other being either right ascension or hour angle. Declination in astronomy is comparable to geographic latitude, but projected onto the celestial sphere. Declination is measured in degrees north and...
, leaving less for the component in right ascension
Right ascension
Right ascension is the astronomical term for one of the two coordinates of a point on the celestial sphere when using the equatorial coordinate system. The other coordinate is the declination.-Explanation:...
, which is the only component that affects the duration of the solar day. As a consequence of that, the daily shift of the shadow cast by the Sun in a sundial, due to obliquity, is smaller close to the equinox
Equinox
An equinox occurs twice a year, when the tilt of the Earth's axis is inclined neither away from nor towards the Sun, the center of the Sun being in the same plane as the Earth's equator...
es and greater close to the solstice
Solstice
A solstice is an astronomical event that happens twice each year when the Sun's apparent position in the sky, as viewed from Earth, reaches its northernmost or southernmost extremes...
s. At the equinoxes, the Sun is seen slowing down by up to 20.3 seconds every day and at the solstices speeding up by the same amount.
In the figure on the right, we can see the monthly variation of the apparent slope of the plane of the ecliptic at solar midday as seen from Earth. This variation is due to the apparent precession
Precession
Precession is a change in the orientation of the rotation axis of a rotating body. It can be defined as a change in direction of the rotation axis in which the second Euler angle is constant...
of the rotating Earth through the year, as seen from the Sun at solar midday.
In terms of the equation of time, the inclination of the ecliptic results in the contribution of another sine wave variation with an amplitude of 9.87 minutes and a period of a half year to the equation of time. The zero points of this sine wave are reached at the equinoxes and solstices, while the maxima are at the beginning of February and August (negative) and the beginning of May and November (positive).
Secular effects
The two above mentioned factors have different wavelengths, amplitudes and phases, so their combined contribution is an irregular wave. At epochEpoch (astronomy)
In astronomy, an epoch is a moment in time used as a reference point for some time-varying astronomical quantity, such as celestial coordinates, or elliptical orbital elements of a celestial body, where these are subject to perturbations and vary with time...
2000 these are the values (in minutes and seconds with UT
Universal Time
Universal Time is a time scale based on the rotation of the Earth. It is a modern continuation of Greenwich Mean Time , i.e., the mean solar time on the Prime Meridian at Greenwich, and GMT is sometimes used loosely as a synonym for UTC...
dates):
| minimum | −14:15 | 11 February |
| zero | 00:00 | 15 April |
| maximum | +03:41 | 14 May |
| zero | 00:00 | 13 June |
| minimum | −06:30 | 26 July |
| zero | 00:00 | 1 September |
| maximum | +16:25 | 3 November |
| zero | 00:00 | 25 December |
E.T. = apparent − mean. Positive means: Sun runs fast and culminates earlier, or the sundial is ahead of mean time. A slight yearly variation occurs due to presence of leap years, resetting itself every 4 years.
The exact shape of the equation of time curve and the associated analemma
Analemma
In astronomy, an analemma is a curve representing the angular offset of a celestial body from its mean position on the celestial sphere as viewed from another celestial body relative to the viewing body's celestial equator...
slowly changes over the centuries due to secular variations in both eccentricity and obliquity. At this moment both are slowly decreasing, but they increase and decrease over a timescale of hundreds of thousands of years. If/when the Earth's orbital eccentricity (now about 0.0167 and slowly decreasing) reaches 0.047, the eccentricity effect may in some circumstances overshadow the obliquity effect, leaving the equation of time curve with only one maximum and minimum per year, as is the case on Mars.
On shorter timescales (thousands of years) the shifts in the dates of equinox and perihelion will be more important. The former is caused by precession
Precession
Precession is a change in the orientation of the rotation axis of a rotating body. It can be defined as a change in direction of the rotation axis in which the second Euler angle is constant...
, and shifts the equinox backwards compared to the stars. But it can be ignored in the current discussion as our Gregorian calendar
Gregorian calendar
The Gregorian calendar, also known as the Western calendar, or Christian calendar, is the internationally accepted civil calendar. It was introduced by Pope Gregory XIII, after whom the calendar was named, by a decree signed on 24 February 1582, a papal bull known by its opening words Inter...
is constructed in such a way as to keep the vernal equinox date at 21 March (at least at sufficient accuracy for our aim here). The shift of the perihelion is forwards, about 1.7 days every century. In 1246 the perihelion occurred on 22 December, the day of the solstice, so the two contributing waves had common zero points and the equation of time curve was symmetrical: in Astronomical Algorithms Meeus gives February and November "maxima" of 15 min 39 sec and May and July of 4 min 58 sec. Before that time the February minimum was larger than the November maximum, and the May maximum larger than the July minimum. The secular change is evident when one compares a current graph of the equation of time (see below) with one from 2000 years ago, for example, one constructed from the data of Ptolemy.
Practical use
If the gnomonGnomon
The gnomon is the part of a sundial that casts the shadow. Gnomon is an ancient Greek word meaning "indicator", "one who discerns," or "that which reveals."It has come to be used for a variety of purposes in mathematics and other fields....
(the shadow-casting object) is not an edge but a point (e.g., a hole in a plate), the shadow (or spot of light) will trace out a curve during the course of a day. If the shadow is cast on a plane surface, this curve will (usually) be the conic section
Conic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
of the hyperbola, since the circle of the Sun's motion
together with the gnomon point define a cone. At the spring and fall equinoxes, the cone degenerates into a plane and the hyperbola into a line. With a different hyperbola for each day, hour marks can be put on each hyperbola which include any necessary corrections. Unfortunately, each hyperbola corresponds to two different days, one in each half of the year, and these two days will require different corrections. A convenient compromise is to draw the line for the "mean time" and add a curve showing the exact position of the shadow points at noon during the course of the year. This curve will take the form of a figure eight and is known as an "analemma
Analemma
In astronomy, an analemma is a curve representing the angular offset of a celestial body from its mean position on the celestial sphere as viewed from another celestial body relative to the viewing body's celestial equator...
". By comparing the analemma to the mean noon line, the amount of correction to be applied generally on that day can be determined.
Detailed calculation
In terms of the right ascensionRight ascension
Right ascension is the astronomical term for one of the two coordinates of a point on the celestial sphere when using the equatorial coordinate system. The other coordinate is the declination.-Explanation:...
of the Sun, , and that of a mean Sun moving uniformly along the celestial equator, M, the equation of time is defined as the difference, = M - . In this expression is the time difference between apparent solar time (time measured by a sundial
Sundial
A sundial is a device that measures time by the position of the Sun. In common designs such as the horizontal sundial, the sun casts a shadow from its style onto a surface marked with lines indicating the hours of the day. The style is the time-telling edge of the gnomon, often a thin rod or a...
) and mean solar time (time measured by a mechanical clock). The left side of this equation is a time difference while the right side terms are angles; however, astronomers regard time and angle as quantities that are related by conversion factors such as; 2 radian = 360 = 1 day = 24 hour. The difference, , is measureable because can be measured and
M, by definition, is a linear function of mean solar time.
The equation of time can be calculated based on Newton's theory of celestial motion in which the earth and sun describe elliptical orbits about their common mass center. In doing this it is usual to write
M = 2t/tY =
where
- t is dynamical time, the independent variable in the theory,
- tY is the length of time in a tropical yearTropical yearA tropical year , for general purposes, is the length of time that the Sun takes to return to the same position in the cycle of seasons, as seen from Earth; for example, the time from vernal equinox to vernal equinox, or from summer solstice to summer solstice...
, is the ecliptic longitude of a dynamical mean Sun; the angle from the vernal equinox to a fictitious Sun moving uniformly along the eclipticEclipticThe ecliptic is the plane of the earth's orbit around the sun. In more accurate terms, it is the intersection of the celestial sphere with the ecliptic plane, which is the geometric plane containing the mean orbit of the Earth around the Sun...
and coinciding with the apparent sun at apoapsis and periapsis.
Substituting into the equation of time, it becomes

The new angles appearing here are: is the mean anomaly
Mean anomaly
In celestial mechanics, the mean anomaly is a parameter relating position and time for a body moving in a Kepler orbit. It is based on the fact that equal areas are swept at the focus in equal intervals of time....
; the angle from the periapsis to the dynamical mean Sun, = - M = 4.9412 = 283.11 is the ecliptic longitude of the periapsis written with its value on 1 Jan 2010 at 12 noon.
However, the displayed equation is approximate; it is not accurate over very long times because it ignores the distinction between dynamical time and mean solar time. In addition, an elliptical orbit formulation ignores small perturbations due to the moon and other planets. Another complication is that the orbital parameter values change significantly over long times, for example increases by about 1.7 degrees per century. Consequently, calculating using the displayed equation with constant orbital parameters produces accurate results only for sufficiently short times (decades); when compared to more accurate calculations using the Multiyear Computer Interactive Almanac for each day in 2008 it disagrees by as much as 35.2 s. It is possible to write an expression for the equation of time that is valid for centuries, but it is necessarily much more complex.
In order to calculate , and hence , as a function of M, three additional angles are required; they are
- E the Sun's eccentric anomalyEccentric anomalyIn celestial mechanics, the eccentric anomaly is an angular parameter that defines the position of a body that is moving along an elliptic Kepler orbit.For the point P orbiting around an ellipse, the eccentric anomaly is the angle E in the figure...
, the Sun's true anomalyTrue anomalyIn celestial mechanics, the true anomaly is an angular parameter that defines the position of a body moving along a Keplerian orbit. It is the angle between the direction of periapsis and the current position of the body, as seen from the main focus of the ellipse .The true anomaly is usually...
, = + the Sun's true longitude on the ecliptic.
All these angles are shown in the figure on the right, which shows the celestial sphere
Celestial sphere
In astronomy and navigation, the celestial sphere is an imaginary sphere of arbitrarily large radius, concentric with the Earth and rotating upon the same axis. All objects in the sky can be thought of as projected upon the celestial sphere. Projected upward from Earth's equator and poles are the...
and the Sun's elliptical orbit seen from the Earth (the same as the Earth's orbit seen from the Sun). In this figure = 0.40907 = 23.438 is the obliquity, while the eccentricity
Eccentricity (mathematics)
In mathematics, the eccentricity, denoted e or \varepsilon, is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular.In particular,...
of the ellipse is e = [1 − (b/a)2]1/2 = 0.016705.
Now given a value of , one can calculate (M) by means of the following procedure:
First, knowing M, calculate E from Kepler's equation
Kepler's equation
Kepler's equation is M = E -\epsilon \cdot \sin E ,where M is the mean anomaly, E is the eccentric anomaly, and \displaystyle \epsilon is the eccentricity....

A numerical value can be obtained from an infinite series, graphical, or numerical methods. Alternatively, note that for e = 0, E = M, and for small e, by iteration, E ~ M + e sin M. This can be improved by iterating again, but for the small value of e that characterises the orbit this approximation is sufficient.
Next, knowing E, calculate the true anomaly
True anomaly
In celestial mechanics, the true anomaly is an angular parameter that defines the position of a body moving along a Keplerian orbit. It is the angle between the direction of periapsis and the current position of the body, as seen from the main focus of the ellipse .The true anomaly is usually...
from an elliptical orbit relation

The correct branch of the multiple valued function tan−1x to use is the one that makes a continuous function of E(M) starting from (E=0) = 0. Thus for 0 E < use tan−1x = Tan−1x, and for < E 2 use tan−1x = Tan−1x + . At the specific value E = for which the argument of tan is infinite, use = E. Here Tan−1x is the principal branch, |Tan−1x| < /2; the function that is returned by calculators and computer applications. Alternatively, note that for e = 0, = E and for small e, from a one term Taylor expansion, ~ E+e sin E ~ M +2 e sin M.
Next knowing ν calculate λ from its definition above

The value of varies non-linearly with M because the orbit is elliptical, from the approximation for , ~ M + p + 2 e sin M.
Next, knowing calculate from a relation for the right triangle on the celestial sphere shown above

Like previously, here the correct branch of tan−1x to use makes a continuous function of (M) starting from (=0)=0. Thus for (2k-1)/2 < < (2k+1)/2, use tan−1x = Tan−1x + k, while for the values = (2k+1)/2 at which the argument of tan is infinite use = . Since + 2 when M varies from 0 to 2, the values of k that are needed, with = 4.9412, are 2, 3, and 4. Although an approximate value for can be obtained from a one term Taylor expansion like that for , it is more efficatious to use the equation
sin( - ) = - tan2(/2) sin( + ). Note that for = 0, = and for small , by iteration, ~ - tan2(/2) sin 2 ~ M + p + 2e sin M - tan2(/2) sin(2M+2p).
Finally, t can be calculated using the starting value of M and the calculated (M). The result is usually given as either a set of tabular values, or a graph of t as a function of the number of days past periapsis, n, where (365.242 is the number of days in a tropical year
Tropical year
A tropical year , for general purposes, is the length of time that the Sun takes to return to the same position in the cycle of seasons, as seen from Earth; for example, the time from vernal equinox to vernal equinox, or from summer solstice to summer solstice...
); so that

Approximation
Using the approximation for (M), t can be written as a simple explicit expression, which is designated because it is only an approximation.
This equation was first derived by Milne, who wrote it in terms of = M + . The numerical values written here result from using the orbital parameter values for e, , and p given previously in this section. When evaluating the numerical expression for ta as given above, a calculator must be in radian mode to obtain correct values. Note also that the date and time of periapsis (perihelion of the Earth orbit) varies from year to year; a table giving the connection can be found in perihelion.
A comparative plot of the two calculations is shown in the figure below. The simpler calculation is seen to be close to the elaborate one, the absolute error, Err = |(t− ta)|, is less than 45 seconds throughout the year; its largest value is 44.8 sec and occurs on day 273. More accurate approximations can be obtained by retaining higher order terms, but they are necessarily more time consuming to evaluate. At some point it is simpler to just evaluate , but ta as written above is easy to evaluate, even with a calculator, and has a nice physical explanation as the sum of two terms, one due to obliquity and the other to eccentricity. This is not true either for considered as a function of M or for higher order approximations of ta.
Alternative approximation
Another calculation for the equation of time can be done as follows. Angles are in degrees.
W is the Earth's mean angular orbital velocity in degrees per day.

where D is the date, in days starting at zero on January 1. 10 is the approximate number of days from the December solstice to January 1. "A" is the angle the earth would move on its orbit at its average speed from the December solstice to date D.

where B is the angle the Earth moves from the solstice to date D, including a first-order correction for the Earth's orbital eccentricity, 0.0167. The number 12 is the number of days from the solstice to the date of the Earth's perihelion.

where C is the difference between the angles moved at mean speed, and at the corrected speed projected onto the equatorial plane, and divided by 180 to get the difference in "half turns". The number 23.44 is the obliquity (tilt) of the Earth's axis. The subtraction gives the conventional sign to the equation of time. Since arctangent has many values, it may cause C to be wrong by an integer number of half turns. The excess half turns can be removed by

where EoT is the equation of time in minutes. The expression nint(C) means the nearest integer to C. On a computer, it can be programmed, for example, as INT(C+0.5). It is 0, 1, or 2 at different times of the year. 720 is the number of minutes (12 hours) that the Earth takes to rotate one half turn relative to the Sun.
Compared with published values , this calculation has a Root Mean Square error of only 3.7 seconds of time. The greatest error is 6.0 seconds. This is much more accurate than the "Approximation" described above, but not as accurate as the "Detailed calculation".
The value of B is an accurate value for the ecliptic longitude (shifted by 90 degrees) so that the Sun's declination becomes readily available:

which is accurate to within a fraction of a degree. See Declination
Declination
In astronomy, declination is one of the two coordinates of the equatorial coordinate system, the other being either right ascension or hour angle. Declination in astronomy is comparable to geographic latitude, but projected onto the celestial sphere. Declination is measured in degrees north and...
article.
External links
- Graphical Visualisation of Equation of Time - Constantly updated
- NOAA Solar Calculator
- USNO rise/set/transit times of the Sun (and other celestial objects)
- The equation of time described on the Royal Greenwich Observatory website
- An analemma site with many illustrations
- The Equation of Time and the Analemma, by Kieron Taylor
- An article by Brian Tung containing a link to a C program using a more accurate formula than most (particularly at high inclinations and eccentricities). The program can calculate solar declination, Equation of Time, or Analemma.
- Doing calculations using Ptolemy's geocentric planetary models with a discussion of his E.T. graph
- Cosmology and the Equation of Time by Jack Forster. Watches that include the equation of time.
- Equation of Time Longcase Clock by John Topping C.1720
- Table giving the Equation of Time and the declination of the sun for every day of the year
- The equation of time correction-table A page describing how to correct a clock to a sundial.
- Solar tempometer - Calculate your solar time including the equation of time.

