
True anomaly
Encyclopedia
In celestial mechanics
, the true anomaly is an angular parameter
that defines the position of a body moving along a Keplerian orbit. It is the angle between the direction of periapsis and the current position of the body, as seen from the main focus of the ellipse
(the point around which the object orbits).
The true anomaly is usually denoted by the Greek letters
 or
or  , or the Roman letter
, or the Roman letter 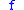 .
.
The true anomaly is one of three angular parameters ("anomalies") that define a position along an orbit; the other two being the eccentric anomaly
and the mean anomaly
.
 can be calculated from orbital state vectors
can be calculated from orbital state vectors
as:
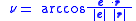 (if
(if 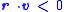 then replace
then replace  by
by  )
)
where:
s the true anomaly is undefined because circular orbits do not have a uniquely determined periapsis. Instead one uses the argument of latitude
u:
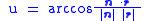 (if
(if 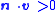 then replace
then replace  by
by  )
)
where:
s with zero inclination the argument of latitude is also undefined, because there is no uniquely determined line of nodes. One uses the true longitude
instead:
 (if
(if  then replace
then replace  by
by  )
)
where:
 and the eccentric anomaly
and the eccentric anomaly
E is:
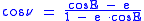
or equivalently
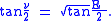
Therefore
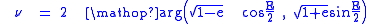
where is the polar argument of the vector
is the polar argument of the vector 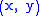 (available in many programming languages as the library function atan2(y, x)
(available in many programming languages as the library function atan2(y, x)
, beware that the arguments are usually in reversed order).

where a is the orbit's semi-major axis
(segment cz).
Celestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of celestial objects. The field applies principles of physics, historically classical mechanics, to astronomical objects such as stars and planets to produce ephemeris data. Orbital mechanics is a subfield which focuses on...
, the true anomaly is an angular parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
that defines the position of a body moving along a Keplerian orbit. It is the angle between the direction of periapsis and the current position of the body, as seen from the main focus of the ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
(the point around which the object orbits).
The true anomaly is usually denoted by the Greek letters
Greek alphabet
The Greek alphabet is the script that has been used to write the Greek language since at least 730 BC . The alphabet in its classical and modern form consists of 24 letters ordered in sequence from alpha to omega...
 or
or  , or the Roman letter
, or the Roman letter 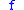 .
.The true anomaly is one of three angular parameters ("anomalies") that define a position along an orbit; the other two being the eccentric anomaly
Eccentric anomaly
In celestial mechanics, the eccentric anomaly is an angular parameter that defines the position of a body that is moving along an elliptic Kepler orbit.For the point P orbiting around an ellipse, the eccentric anomaly is the angle E in the figure...
and the mean anomaly
Mean anomaly
In celestial mechanics, the mean anomaly is a parameter relating position and time for a body moving in a Kepler orbit. It is based on the fact that equal areas are swept at the focus in equal intervals of time....
.
From state vectors
For elliptic orbits true anomaly can be calculated from orbital state vectors
can be calculated from orbital state vectorsOrbital state vectors
In astrodynamics or celestial dynamics orbital state vectors are vectors of position and velocity that together with their time uniquely determine the state of an orbiting body....
as:
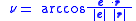 (if
(if 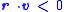 then replace
then replace  by
by  )
)where:
-
 is orbital velocity vector of the orbiting body,
is orbital velocity vector of the orbiting body, -
 is eccentricity vectorEccentricity vectorIn astrodynamics, the eccentricity vector of a Kepler orbit is the vector pointing towards the periapsis having a magnitude equal to the orbit's scalar eccentricity. The magnitude is unitless. For Kepler orbits the eccentricity vector is a constant of motion...
is eccentricity vectorEccentricity vectorIn astrodynamics, the eccentricity vector of a Kepler orbit is the vector pointing towards the periapsis having a magnitude equal to the orbit's scalar eccentricity. The magnitude is unitless. For Kepler orbits the eccentricity vector is a constant of motion...
, -
 is orbital position vector (segment fp) of the orbiting body.
is orbital position vector (segment fp) of the orbiting body.
Circular orbit
For circular orbitCircular orbit
A circular orbit is the orbit at a fixed distance around any point by an object rotating around a fixed axis.Below we consider a circular orbit in astrodynamics or celestial mechanics under standard assumptions...
s the true anomaly is undefined because circular orbits do not have a uniquely determined periapsis. Instead one uses the argument of latitude
Argument of latitude
In celestial mechanics, the argument of latitude is an angular parameter that defines the position of a body moving along a Kepler orbit. It is the sum of the more commonly used true anomaly and argument of periapsis. u = \nu + \omega...
u:
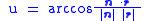 (if
(if 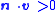 then replace
then replace  by
by  )
)where:
-
 is vector pointing towards the ascending node (i.e. the z-component of
is vector pointing towards the ascending node (i.e. the z-component of  is zero).
is zero).
Circular orbit with zero inclination
For circular orbitCircular orbit
A circular orbit is the orbit at a fixed distance around any point by an object rotating around a fixed axis.Below we consider a circular orbit in astrodynamics or celestial mechanics under standard assumptions...
s with zero inclination the argument of latitude is also undefined, because there is no uniquely determined line of nodes. One uses the true longitude
True longitude
In astrodynamics true longitude is the longitude at which an orbiting body could actually be found if its inclination were zero. Together with the inclination and the ascending node, the true longitude can tell us the precise direction from the central object at which the body would be located at...
instead:
 (if
(if  then replace
then replace  by
by  )
)where:
-
 is x-component of orbital position vector
is x-component of orbital position vector  ,
, -
 is x-component of orbital velocity vector
is x-component of orbital velocity vector  .
.
From the eccentric anomaly
The relation between the true anomaly and the eccentric anomaly
and the eccentric anomalyEccentric anomaly
In celestial mechanics, the eccentric anomaly is an angular parameter that defines the position of a body that is moving along an elliptic Kepler orbit.For the point P orbiting around an ellipse, the eccentric anomaly is the angle E in the figure...
E is:
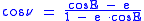
or equivalently
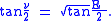
Therefore
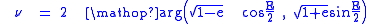
where
 is the polar argument of the vector
is the polar argument of the vector 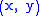 (available in many programming languages as the library function atan2(y, x)
(available in many programming languages as the library function atan2(y, x)Atan2
In trigonometry, the two-argument function atan2 is a variation of the arctangent function. For any real arguments and not both equal to zero, is the angle in radians between the positive -axis of a plane and the point given by the coordinates on it...
, beware that the arguments are usually in reversed order).
Radius from true anomaly
The radius (distance from the focus of attraction and the orbiting body) is related to the true anomaly by the formula
where a is the orbit's semi-major axis
Semi-major axis
The major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
(segment cz).
See also
- Kepler's laws of planetary motionKepler's laws of planetary motionIn astronomy, Kepler's laws give a description of the motion of planets around the Sun.Kepler's laws are:#The orbit of every planet is an ellipse with the Sun at one of the two foci....
- Eccentric anomalyEccentric anomalyIn celestial mechanics, the eccentric anomaly is an angular parameter that defines the position of a body that is moving along an elliptic Kepler orbit.For the point P orbiting around an ellipse, the eccentric anomaly is the angle E in the figure...
- Mean anomalyMean anomalyIn celestial mechanics, the mean anomaly is a parameter relating position and time for a body moving in a Kepler orbit. It is based on the fact that equal areas are swept at the focus in equal intervals of time....
- EllipseEllipseIn geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
- HyperbolaHyperbolaIn mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...

