Mean anomaly
Encyclopedia
In celestial mechanics
, the mean anomaly is a parameter
relating position and time for a body moving in a Kepler orbit
. It is based on the fact that equal areas are swept at the focus in equal intervals of time.
The mean anomaly increases uniformly from 0 to
radians during each orbit. However, it is not an angle. Due to Kepler's second law, the mean anomaly is proportional to the area swept by the focus
-to-body line since the last periapsis.
The mean anomaly is usually denoted by the letter
, and is given by the formula:
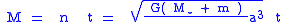
where n is the mean motion
, a is the length of the orbit's semi-major axis
,
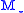and m are the orbiting masses, and G is the gravitational constant
.
The mean anomaly is the time since the last periapsis multiplied by the mean motion
, and the mean motion is
divided by the duration of a full orbit
.
The mean anomaly is one of three angular parameters ("anomalies") that define a position along an orbit; the other two being the eccentric anomaly
and the true anomaly
. If the mean anomaly is known at any given instant, it can be calculated at any later (or prior instant) by simply adding (or subtracting)
where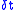 
represents the time difference. The other anomalies can hence be calculated.
E and the eccentricity
e with Kepler's Equation
:
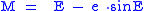
To find the position of the object in an elliptic Kepler orbit at a given time t, the mean anomaly is found by multiplying the time and the mean motion, then it is used to find the eccentric anomaly by solving Kepler's equation.
It is also frequently seen:
,
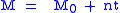Again n is the mean motion. However, t, in this instance, is the time since epoch, which is how much time has passed since the measurement of M0 was taken. The value M0 denotes the mean anomaly at epoch, which is the mean anomaly at the time the measurement was taken.
Celestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of celestial objects. The field applies principles of physics, historically classical mechanics, to astronomical objects such as stars and planets to produce ephemeris data. Orbital mechanics is a subfield which focuses on...
, the mean anomaly is a parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
relating position and time for a body moving in a Kepler orbit
Kepler orbit
In celestial mechanics, a Kepler orbit describes the motion of an orbiting body as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space...
. It is based on the fact that equal areas are swept at the focus in equal intervals of time.
The mean anomaly increases uniformly from 0 to
radians during each orbit. However, it is not an angle. Due to Kepler's second law, the mean anomaly is proportional to the area swept by the focusFocus (geometry)
In geometry, the foci are a pair of special points with reference to which any of a variety of curves is constructed. For example, foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola...
-to-body line since the last periapsis.
The mean anomaly is usually denoted by the letter
, and is given by the formula: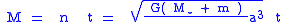where n is the mean motion
Mean motion
Mean motion, n\,\!, is a measure of how fast a satellite progresses around its elliptical orbit. Unless the orbit is circular, the mean motion is only an average value, and does not represent the instantaneous angular rate....
, a is the length of the orbit's semi-major axis
Semi-major axis
The major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
,
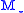and m are the orbiting masses, and G is the gravitational constantGravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
.
The mean anomaly is the time since the last periapsis multiplied by the mean motion
Mean motion
Mean motion, n\,\!, is a measure of how fast a satellite progresses around its elliptical orbit. Unless the orbit is circular, the mean motion is only an average value, and does not represent the instantaneous angular rate....
, and the mean motion is
divided by the duration of a full orbitOrbital period
The orbital period is the time taken for a given object to make one complete orbit about another object.When mentioned without further qualification in astronomy this refers to the sidereal period of an astronomical object, which is calculated with respect to the stars.There are several kinds of...
.
The mean anomaly is one of three angular parameters ("anomalies") that define a position along an orbit; the other two being the eccentric anomaly
Eccentric anomaly
In celestial mechanics, the eccentric anomaly is an angular parameter that defines the position of a body that is moving along an elliptic Kepler orbit.For the point P orbiting around an ellipse, the eccentric anomaly is the angle E in the figure...
and the true anomaly
True anomaly
In celestial mechanics, the true anomaly is an angular parameter that defines the position of a body moving along a Keplerian orbit. It is the angle between the direction of periapsis and the current position of the body, as seen from the main focus of the ellipse .The true anomaly is usually...
. If the mean anomaly is known at any given instant, it can be calculated at any later (or prior instant) by simply adding (or subtracting)
where 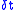represents the time difference. The other anomalies can hence be calculated.Formulas
The mean anomaly M can be computed from the eccentric anomalyEccentric anomaly
In celestial mechanics, the eccentric anomaly is an angular parameter that defines the position of a body that is moving along an elliptic Kepler orbit.For the point P orbiting around an ellipse, the eccentric anomaly is the angle E in the figure...
E and the eccentricity
Eccentricity (mathematics)
In mathematics, the eccentricity, denoted e or \varepsilon, is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular.In particular,...
e with Kepler's Equation
Kepler's equation
Kepler's equation is M = E -\epsilon \cdot \sin E ,where M is the mean anomaly, E is the eccentric anomaly, and \displaystyle \epsilon is the eccentricity....
:
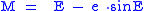
To find the position of the object in an elliptic Kepler orbit at a given time t, the mean anomaly is found by multiplying the time and the mean motion, then it is used to find the eccentric anomaly by solving Kepler's equation.
It is also frequently seen:
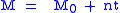,Again n is the mean motion. However, t, in this instance, is the time since epoch, which is how much time has passed since the measurement of M0 was taken. The value M0 denotes the mean anomaly at epoch, which is the mean anomaly at the time the measurement was taken.