Orthorhombic crystal system - AbsoluteAstronomy.com

Crystallography

Crystallography is the experimental science of the arrangement of atoms in solids. The word "crystallography" derives from the Greek words crystallon = cold drop / frozen drop, with its meaning extending to all solids with some degree of transparency, and grapho = write.Before the development of...

, the orthorhombic crystal system

Crystal system

In crystallography, the terms crystal system, crystal family, and lattice system each refer to one of several classes of space groups, lattices, point groups, or crystals...

is one of the seven lattice point group

Point group

In geometry, a point group is a group of geometric symmetries that keep at least one point fixed. Point groups can exist in a Euclidean space with any dimension, and every point group in dimension d is a subgroup of the orthogonal group O...

s. Orthorhombic lattice

Lattice (group)

In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...

s result from stretching a cubic lattice

Cubic lattice

Cubic lattice may refer to:*Cubic crystal system*Cubic honeycomb*Integer lattice...

along two of its orthogonal pairs by two different factors, resulting in a rectangular prism

Prism (geometry)

In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...

with a rectangular base

Radix

In mathematical numeral systems, the base or radix for the simplest case is the number of unique digits, including zero, that a positional numeral system uses to represent numbers. For example, for the decimal system the radix is ten, because it uses the ten digits from 0 through 9.In any numeral...

(a by b) and height (c), such that a, b, and c are distinct. All three bases intersect at 90° angles. The three lattice vectors remain mutually orthogonal.

Bravais Lattices

There are four orthorhombic Bravais lattices: simple orthorhombic, base-centered orthorhombic, body-centered orthorhombic, and face-centered orthorhombic.

Orthorhombic Bravais lattices
Primitive	Body-centered	Base-centered	Face-centered

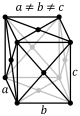Crystal Classes

The orthorhombic crystal system class names, examples, Schönflies notation, Hermann-Mauguin notation

Hermann-Mauguin notation

Hermann–Mauguin notation is used to represent the symmetry elements in point groups, plane groups and space groups. It is named after the German crystallographer Carl Hermann and the French mineralogist Charles-Victor Mauguin...

, point groups

Crystallographic point group

In crystallography, a crystallographic point group is a set of symmetry operations, like rotations or reflections, that leave a central point fixed while moving other directions and faces of the crystal to the positions of features of the same kind...

, International Tables for Crystallography space group number, orbifold

Orbifold

In the mathematical disciplines of topology, geometry, and geometric group theory, an orbifold is a generalization of a manifold...

, type, and space groups are listed in the table below.

#	Point group					Example	Type	Space group Space group In mathematics and geometry, a space group is a symmetry group, usually for three dimensions, that divides space into discrete repeatable domains.In three dimensions, there are 219 unique types, or counted as 230 if chiral copies are considered distinct... s
#	Name	Schönflies Schoenflies notation The Schoenflies notation or Schönflies notation, named after the German mathematician Arthur Moritz Schoenflies, is one of two conventions commonly used to describe Point groups. This notation is used in spectroscopy. The other convention is the Hermann–Mauguin notation, also known as the...	Intl Hermann-Mauguin notation Hermann–Mauguin notation is used to represent the symmetry elements in point groups, plane groups and space groups. It is named after the German crystallographer Carl Hermann and the French mineralogist Charles-Victor Mauguin...	Orbifold Orbifold In the mathematical disciplines of topology, geometry, and geometric group theory, an orbifold is a generalization of a manifold...	Coxeter Coxeter notation In geometry, Coxeter notation is a system of classifying symmetry groups, describing the angles between with fundamental reflections of a Coxeter group. It uses a bracketed notation, with modifiers to indicate certain subgroups. The notation is named after H. S. M...	Example	Type
16-24	sphenoidal	D₂	222	222	[2,2]⁺	epsomite Epsomite Epsomite is a hydrous magnesium sulfate mineral with formula MgSO4·7H2O or simply MgSO4. Epsomite forms as encrustations or efflorescences on limestone cavern walls and mine timbers and walls, as a volcanic fumaroles, and as rare beds in evaporate layers...	enantiomorphic	P222, P222₁, P2₁2₁2, P2₁2₁2₁, C222₁, C222, F222, I222, I2₁2₁2₁
25-46	pyramidal	C_2v	mm2	*22	[2]	hemimorphite Hemimorphite Hemimorphite, is a sorosilicate mineral which has been mined from days of old from the upper parts of zinc and lead ores, chiefly associated with smithsonite. It was often assumed to be the same mineral and both were classed under the same name of calamine... , bertrandite Bertrandite Bertrandite is a beryllium sorosilicate hydroxide mineral with composition: Be4Si2O72. Bertrandite is a colorless to pale yellow orthorhombic mineral with a hardness of 6-7. It is commonly found in beryllium rich pegmatites and is in part an alteration of beryl. Bertrandite often occurs as a...	polar Polar - Science, technology, and mathematics :Polar , a satellite launched by NASA in 1996Polar , a strongly magnetic cataclysmic variable star system...	Pmm2, Pmc2₁, Pcc2, Pma2, Pca2₁, Pnc2, Pmn2₁, Pba2, Pna2₁, Pnn2, Cmm2, Cmc2₁, Ccc2, Amm2, Aem2, Ama2,Aea2, Fmm2, Fdd2, Imm2, Iba2, Ima2
47-74	bipyramidal	D_2h	mmm	*222	[2,2]	olivine Olivine The mineral olivine is a magnesium iron silicate with the formula 2SiO4. It is a common mineral in the Earth's subsurface but weathers quickly on the surface.... , aragonite Aragonite Aragonite is a carbonate mineral, one of the two common, naturally occurring, crystal forms of calcium carbonate, CaCO3... , marcasite Marcasite The mineral marcasite, sometimes called white iron pyrite, is iron sulfide with orthorhombic crystal structure. It is physically and crystallographically distinct from pyrite, which is iron sulfide with cubic crystal structure. Both structures do have in common that they contain the disulfide...	centrosymmetric	Pmmm, Pnnn, Pccm, Pban, Pmma, Pnna, Pmna, Pcca, Pbam, Pccn, Pbcm, Pnnm, Pmmn, Pbcn, Pbca, Pnma, Cmcm, Cmce, Cmmm, Cccm, Cmme, Ccce, Fmmm, Fddd, Immm, Ibam, Ibca, Imma

Bravais Lattices

Crystal Classes

See also