
Hyperelastic material
Encyclopedia
A hyperelastic or Green elastic material is a type of constitutive model
for ideally elastic material for which the stress-strain relationship derives from a strain energy density function
. The hyperelastic material is a special case of a Cauchy elastic material
.
For many materials, linear elastic
models do not accurately describe the observed material behaviour. The most common example of this kind of material is rubber, whose stress
-strain relationship can be defined as non-linearly elastic, isotropic, incompressible and generally independent of strain rate. Hyperelasticity provides a means of modeling the stress-strain behavior of such materials. The behavior of unfilled, vulcanized elastomers often conforms closely to the hyperelastic ideal. Filled elastomers and biological tissues are also often modeled via the hyperelastic idealization.
Ronald Rivlin
and Melvin Mooney
developed the first hyperelastic models, the Neo-Hookean
and Mooney–Rivlin solids. Many other hyperelastic models have since been developed. Other widely used hyperelastic material models include the Ogden
model and the Arruda–Boyce model.
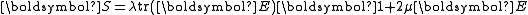
where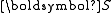 is the second Piola–Kirchhoff stress and
is the second Piola–Kirchhoff stress and 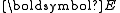 is the Lagrangian Green strain, and
is the Lagrangian Green strain, and  and
and 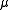 are the Lamé constants.
are the Lamé constants.
The strain-energy density function for the St. Venant–Kirchhoff model is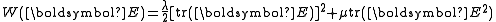
and the second Piola–Kirchhoff stress can be derived from the relation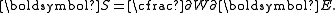
1) phenomenological
descriptions of observed behavior
2) mechanistic models
deriving from arguments about underlying structure of the material
3) hybrids of phenomenological and mechanistic models
 is the strain energy density function, the 1st Piola–Kirchoff stress tensor can be calculated for a hyperelastic material as
is the strain energy density function, the 1st Piola–Kirchoff stress tensor can be calculated for a hyperelastic material as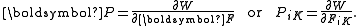
where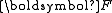 is the deformation gradient. In terms of the Lagrangian Green strain (
is the deformation gradient. In terms of the Lagrangian Green strain (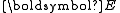 )
)
In terms of the right Cauchy–Green deformation tensor (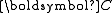 )
)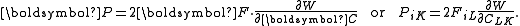
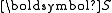 is the second Piola–Kirchhoff stress tensor then
is the second Piola–Kirchhoff stress tensor then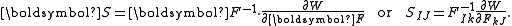
In terms of the Lagrangian Green strain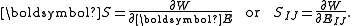
In terms of the right Cauchy–Green deformation tensor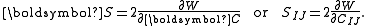
is given by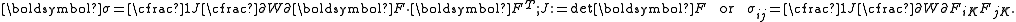
In terms of the Lagrangian Green strain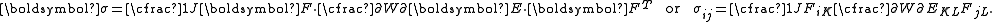
In terms of the right Cauchy–Green deformation tensor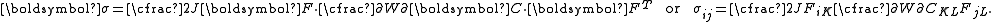
 . The incompressibility constraint is therefore
. The incompressibility constraint is therefore 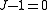 . To ensure incompressibility of a hyperelastic material, the strain-energy function can be written in form:
. To ensure incompressibility of a hyperelastic material, the strain-energy function can be written in form: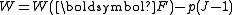
where the hydrostatic pressure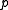 functions as a Lagrangian multiplier
functions as a Lagrangian multiplier
to enforce the incompressibility constraint. The 1st Piola–Kirchoff stress now becomes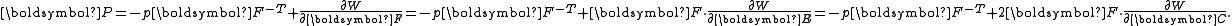
This stress tensor can subsequently be converted
into any of the other conventional stress tensors, such as the Cauchy Stress tensor which is given by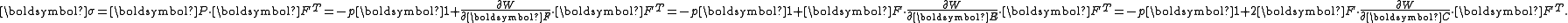
is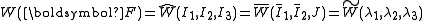 , then
, then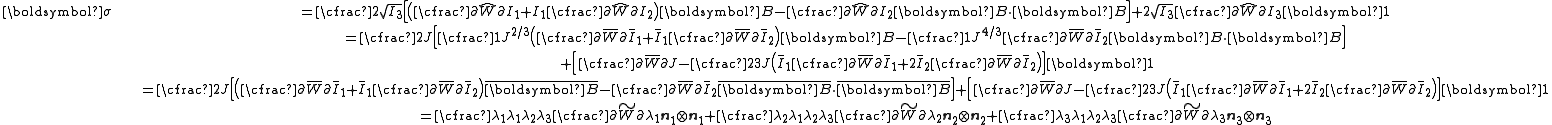
(See the page on the left Cauchy–Green deformation tensor for the definitions of these symbols).
is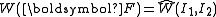 . The Cauchy stress is then given by
. The Cauchy stress is then given by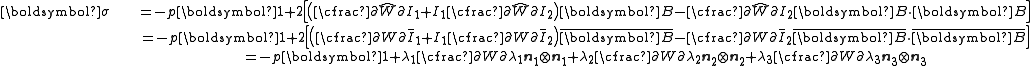
where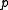 is an undetermined pressure. In terms of stress differences
is an undetermined pressure. In terms of stress differences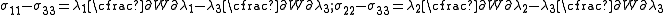
If in addition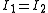 , then
, then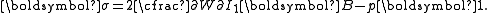
If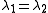 , then
, then
with linearized hyperelasticity at small strains.
, the stress-strain relation should have the following form in the infinitesimal strain limit: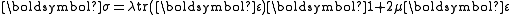
where are the Lame constants. The strain energy density function that corresponds to the above relation is
are the Lame constants. The strain energy density function that corresponds to the above relation is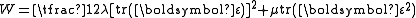
For an incompressible material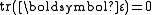 and we have
and we have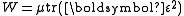
For any strain energy density function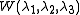 to reduce to the above forms for small strains the following conditions have to be met
to reduce to the above forms for small strains the following conditions have to be met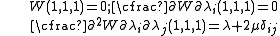
If the material is incompressible then the above conditions may be expressed in the following form.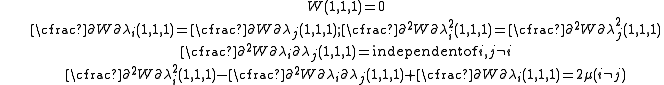
These conditions can be used to find relations between the parameters of a given hyperelastic model and shear and bulk moduli.
Consistency conditions for incompressible
Many elastomers are modeled adequately by a strain energy density function that depends only on 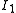 . For such materials we have
. For such materials we have 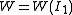 and
and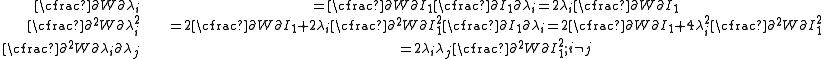
The consistency conditions for incompressible materials for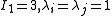 may then be expressed as
may then be expressed as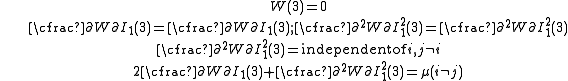
Constitutive equation
In physics, a constitutive equation is a relation between two physical quantities that is specific to a material or substance, and approximates the response of that material to external forces...
for ideally elastic material for which the stress-strain relationship derives from a strain energy density function
Strain energy density function
A strain energy density function or stored energy density function is a scalar valued function that relates the strain energy density of a material to the deformation gradient....
. The hyperelastic material is a special case of a Cauchy elastic material
Cauchy elastic material
A Cauchy-elastic material is one in which the Cauchy stress at each material point is determined only by the current state of deformation . A Cauchy-elastic material is one in which the Cauchy stress at each material point is determined only by the current state of deformation (with respect to an...
.
For many materials, linear elastic
Elasticity (physics)
In physics, elasticity is the physical property of a material that returns to its original shape after the stress that made it deform or distort is removed. The relative amount of deformation is called the strain....
models do not accurately describe the observed material behaviour. The most common example of this kind of material is rubber, whose stress
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
-strain relationship can be defined as non-linearly elastic, isotropic, incompressible and generally independent of strain rate. Hyperelasticity provides a means of modeling the stress-strain behavior of such materials. The behavior of unfilled, vulcanized elastomers often conforms closely to the hyperelastic ideal. Filled elastomers and biological tissues are also often modeled via the hyperelastic idealization.
Ronald Rivlin
Ronald Rivlin
Ronald Samuel Rivlin was a British-American physicist, mathematician, rheologist and a noted expert on rubber.-Life:Rivlin was born in London in 1915. He studied physics and mathematics at St John's College, Cambridge, being awarded a BA in 1937 and a ScD in 1952...
and Melvin Mooney
Melvin Mooney
Melvin Mooney was an American physicist and rheologist.He developed the Mooney Viscometer and other testing equipment used in the rubber industry. He also proposed the Mooney-Rivlin solid constitutive law describing the hyperelastic stress-strain behavior of rubber...
developed the first hyperelastic models, the Neo-Hookean
Neo-Hookean solid
A Neo-Hookean solid is a hyperelastic material model, similar to Hooke's law, that can be used for predicting the nonlinear stress-strain behavior of materials undergoing large deformations. The model was proposed by Ronald Rivlin in 1948. In contrast to linear elastic materials, a the...
and Mooney–Rivlin solids. Many other hyperelastic models have since been developed. Other widely used hyperelastic material models include the Ogden
Ogden (hyperelastic model)
The Ogden material model is a hyperelastic material model used to describe the non-linear stress-strain behaviour of complex materials such as rubbers, polymers, and biological tissue. The model was developed by Ray W. Ogden in 1972...
model and the Arruda–Boyce model.
Saint Venant–Kirchhoff model
The simplest hyperelastic material model is the Saint Venant–Kirchhoff model which is just an extension of the linear elastic material model to the nonlinear regime. This model has the form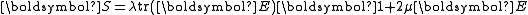
where
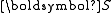 is the second Piola–Kirchhoff stress and
is the second Piola–Kirchhoff stress and 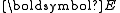 is the Lagrangian Green strain, and
is the Lagrangian Green strain, and  and
and 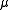 are the Lamé constants.
are the Lamé constants.The strain-energy density function for the St. Venant–Kirchhoff model is
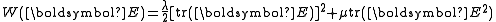
and the second Piola–Kirchhoff stress can be derived from the relation
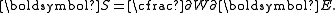
Classification of hyperelastic material models
Hyperelastic material models can be classified as:1) phenomenological
Phenomenology (science)
The term phenomenology in science is used to describe a body of knowledge that relates empirical observations of phenomena to each other, in a way that is consistent with fundamental theory, but is not directly derived from theory. For example, we find the following definition in the Concise...
descriptions of observed behavior
- Fung
- Mooney–Rivlin
- OgdenOgden (hyperelastic model)The Ogden material model is a hyperelastic material model used to describe the non-linear stress-strain behaviour of complex materials such as rubbers, polymers, and biological tissue. The model was developed by Ray W. Ogden in 1972...
- PolynomialPolynomial (hyperelastic model)The polynomial hyperelastic material model is a phenomenological model of rubber elasticity. In this model, the strain energy density function is of the form of a polynomial in the two invariants I_1,I_2 of the left Cauchy-Green deformation tensor....
- Saint Venant–Kirchhoff
- YeohYeoh (hyperelastic model)300px|right|thumb|Yeoh model prediction versus experimental data for natural rubber. Model parameters and experimental data from The Yeoh hyperelastic material model is a phenomenological model for the deformation of nearly incompressible, nonlinear elastic materials such as rubber...
2) mechanistic models
Rubber Elasticity
Rubber elasticity, a well-known example of hyperelasticity, describes the mechanical behavior of many polymers, especially those with crosslinking. Invoking the theory of rubber elasticity, one considers a polymer chain in a crosslinked network as an entropic spring. When the chain is stretched,...
deriving from arguments about underlying structure of the material
- Arruda–Boyce model
- Neo-HookeanNeo-Hookean solidA Neo-Hookean solid is a hyperelastic material model, similar to Hooke's law, that can be used for predicting the nonlinear stress-strain behavior of materials undergoing large deformations. The model was proposed by Ronald Rivlin in 1948. In contrast to linear elastic materials, a the...
3) hybrids of phenomenological and mechanistic models
- GentGent (hyperelastic model)The Gent hyperelastic material model is a phenomenological model of rubber elasticity that is based on the concept of limiting chain extensibility...
First Piola–Kirchhoff stress
If is the strain energy density function, the 1st Piola–Kirchoff stress tensor can be calculated for a hyperelastic material as
is the strain energy density function, the 1st Piola–Kirchoff stress tensor can be calculated for a hyperelastic material as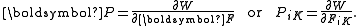
where
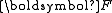 is the deformation gradient. In terms of the Lagrangian Green strain (
is the deformation gradient. In terms of the Lagrangian Green strain (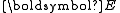 )
)
In terms of the right Cauchy–Green deformation tensor (
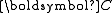 )
)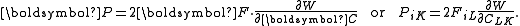
Second Piola–Kirchhoff stress
If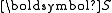 is the second Piola–Kirchhoff stress tensor then
is the second Piola–Kirchhoff stress tensor then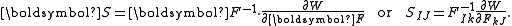
In terms of the Lagrangian Green strain
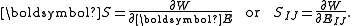
In terms of the right Cauchy–Green deformation tensor
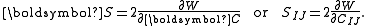
Cauchy stress
Similarly, the Cauchy stressStress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
is given by
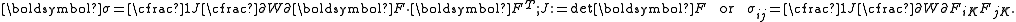
In terms of the Lagrangian Green strain
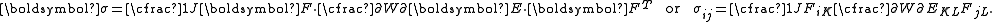
In terms of the right Cauchy–Green deformation tensor
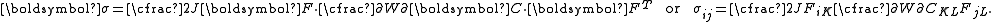
Incompressible hyperelastic materials
For an incompressible material . The incompressibility constraint is therefore
. The incompressibility constraint is therefore 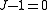 . To ensure incompressibility of a hyperelastic material, the strain-energy function can be written in form:
. To ensure incompressibility of a hyperelastic material, the strain-energy function can be written in form: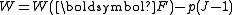
where the hydrostatic pressure
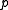 functions as a Lagrangian multiplier
functions as a Lagrangian multiplierLagrange multipliers
In mathematical optimization, the method of Lagrange multipliers provides a strategy for finding the maxima and minima of a function subject to constraints.For instance , consider the optimization problem...
to enforce the incompressibility constraint. The 1st Piola–Kirchoff stress now becomes
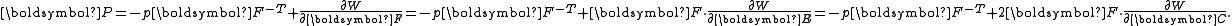
This stress tensor can subsequently be converted
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
into any of the other conventional stress tensors, such as the Cauchy Stress tensor which is given by
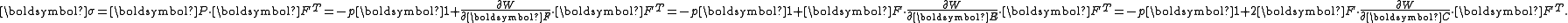
Compressible isotropic hyperelastic materials
For isotropic hyperelastic materials, the Cauchy stress can be expressed in terms of the invariants of the left Cauchy–Green deformation tensor (or right Cauchy–Green deformation tensor). If the strain energy density functionStrain energy density function
A strain energy density function or stored energy density function is a scalar valued function that relates the strain energy density of a material to the deformation gradient....
is
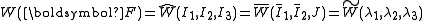 , then
, then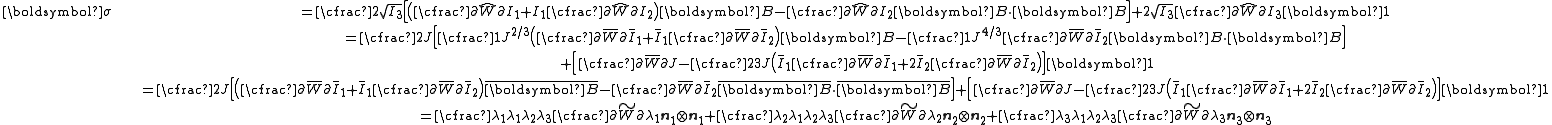
(See the page on the left Cauchy–Green deformation tensor for the definitions of these symbols).
| Proof 1: |
|---|
| The second Piola–Kirchhoff stress tensor Stress (physics) In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body... for a hyperelastic material is given by  where 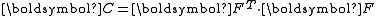 is the right Cauchy–Green deformation tensor and is the right Cauchy–Green deformation tensor and 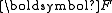 is the deformation gradient. The Cauchy stress is the deformation gradient. The Cauchy stressStress (physics) In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body... is given by  where 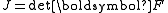 . Let . Let 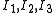 be the three principal invariants of be the three principal invariants of  . Then . Then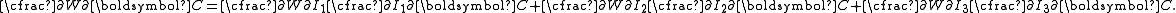 The derivatives of the invariants Tensor derivative (continuum mechanics) The derivatives of scalars, vectors, and second-order tensors with respect to second-order tensors are of considerable use in continuum mechanics. These derivatives are used in the theories of nonlinear elasticity and plasticity, particularly in the design of algorithms for numerical... of the symmetric tensor 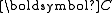 are are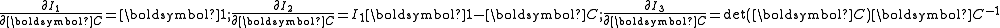 Therefore we can write 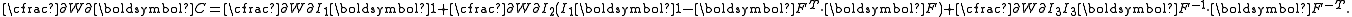 Plugging into the expression for the Cauchy stress gives 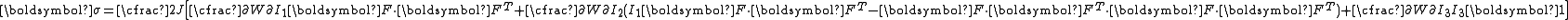 Using the left Cauchy–Green deformation tensor 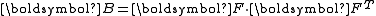 and noting that and noting that 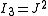 , we can write , we can write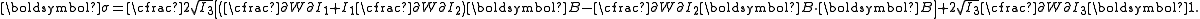 For an incompressible material 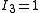 and hence and hence 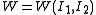 .Then .Then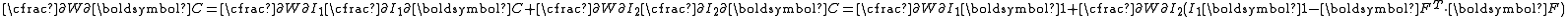 Therefore the Cauchy stress is given by 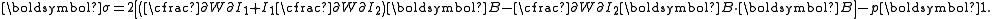 where 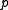 is an undetermined pressure which acts as a Lagrange multiplier to enforce the incompressibility constraint. is an undetermined pressure which acts as a Lagrange multiplier to enforce the incompressibility constraint.If, in addition, 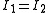 , we have , we have 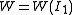 and hence and hence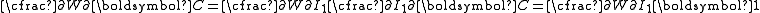 In that case the Cauchy stress can be expressed as 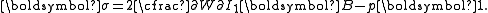 |
| Proof 2: |
|---|
| The isochoric Isochoric Isochoric may refer to:*cell-transitive, in geometry*isochoric process, in chemistry or thermodynamics... deformation gradient is defined as 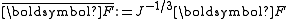 , resulting in the isochoric deformation gradient having a determinant of 1, in other words it is volume stretch free. Using this one can subsequently define the isochoric left Cauchy–Green deformation tensor tensor , resulting in the isochoric deformation gradient having a determinant of 1, in other words it is volume stretch free. Using this one can subsequently define the isochoric left Cauchy–Green deformation tensor tensor 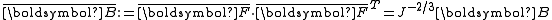 . .The invariants of 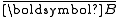 are are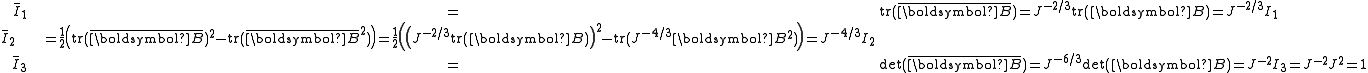 The set of invariants which are used to define the distortional behavior are the first two invariants of the isochoric left Cauchy–Green deformation tensor tensor, (which are identical to the ones for the right Cauchy Green stretch tensor), and add 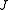 into the fray to describe the volumetric behaviour. into the fray to describe the volumetric behaviour.To express the Cauchy stress in terms of the invariants  recall that recall that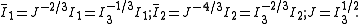 The chain rule of differentiation gives us 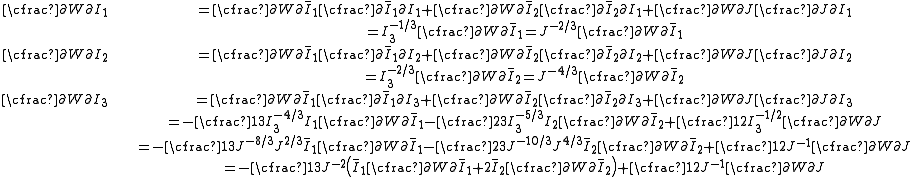 Recall that the Cauchy stress is given by  In terms of the invariants 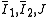 we have we have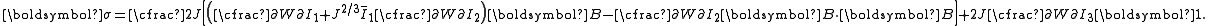 Plugging in the expressions for the derivatives of 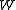 in terms of in terms of 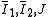 , we have , we have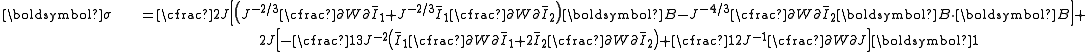 or, 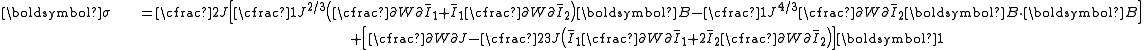 In terms of the deviatoric part of 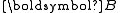 , we can write , we can write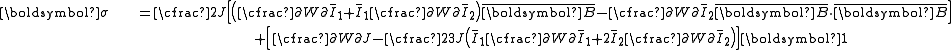 For an incompressible material  and hence and hence 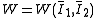 .Then .Thenthe Cauchy stress is given by 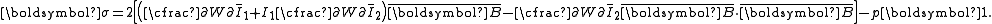 where 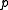 is an undetermined pressure-like Lagrange multiplier term. In addition, if is an undetermined pressure-like Lagrange multiplier term. In addition, if 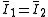 , we have , we have 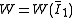 and hence and hencethe Cauchy stress can be expressed as 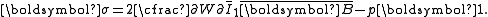 |
| Proof 3: |
|---|
To express the Cauchy stress in terms of the stretches 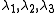 recall that recall that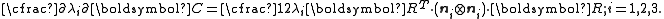 The chain rule gives 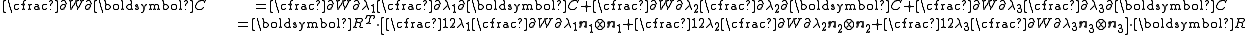 The Cauchy stress is given by 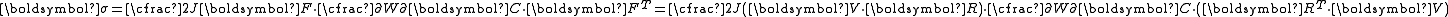 Plugging in the expression for the derivative of 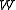 leads to leads to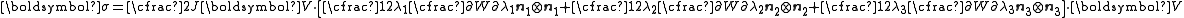 Using the spectral decomposition of  we have we have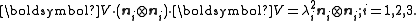 Also note that 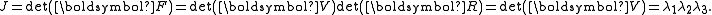 Therefore the expression for the Cauchy stress can be written as  For an incompressible material 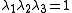 and hence and hence  . Following Ogden p. 485, we may write . Following Ogden p. 485, we may write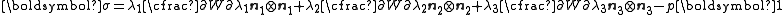 Some care is to required at this stage because, when an eigenvalue is repeated, it is in general only Gateaux differentiable, but not Frechet differentiable. A rigorous tensor derivative Tensor derivative (continuum mechanics) The derivatives of scalars, vectors, and second-order tensors with respect to second-order tensors are of considerable use in continuum mechanics. These derivatives are used in the theories of nonlinear elasticity and plasticity, particularly in the design of algorithms for numerical... can only be found by solving another eigenvalue problem. If we express the stress in terms of differences between components,  If in addition to incompressibility we have  then a possible solution to the problem then a possible solution to the problemrequires 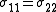 and we can write the stress differences as and we can write the stress differences as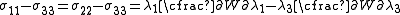 |
Incompressible isotropic hyperelastic materials
For incompressible isotropic hyperelastic materials, the strain energy density functionStrain energy density function
A strain energy density function or stored energy density function is a scalar valued function that relates the strain energy density of a material to the deformation gradient....
is
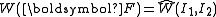 . The Cauchy stress is then given by
. The Cauchy stress is then given by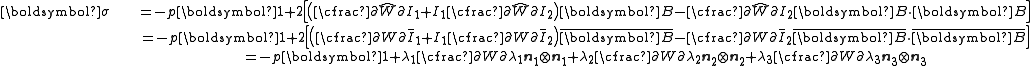
where
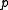 is an undetermined pressure. In terms of stress differences
is an undetermined pressure. In terms of stress differences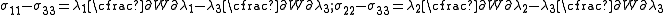
If in addition
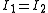 , then
, then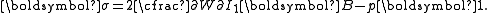
If
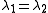 , then
, then
Consistency with linear elasticity
Consistency with linear elasticity is often used to determine some of the parameters of hyperelastic material models. These consistency conditions can be found by comparing Hooke's lawHooke's law
In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
with linearized hyperelasticity at small strains.
Consistency conditions for isotropic hyperelastic models
For isotropic hyperelastic materials to be consistent with isotropic linear elasticityLinear elasticity
Linear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
, the stress-strain relation should have the following form in the infinitesimal strain limit:
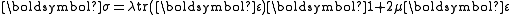
where
 are the Lame constants. The strain energy density function that corresponds to the above relation is
are the Lame constants. The strain energy density function that corresponds to the above relation is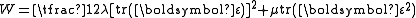
For an incompressible material
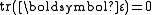 and we have
and we have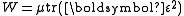
For any strain energy density function
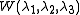 to reduce to the above forms for small strains the following conditions have to be met
to reduce to the above forms for small strains the following conditions have to be met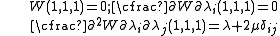
If the material is incompressible then the above conditions may be expressed in the following form.
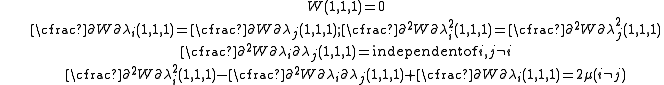
These conditions can be used to find relations between the parameters of a given hyperelastic model and shear and bulk moduli.
Consistency conditions for incompressible  based rubber materials
based rubber materials
Many elastomers are modeled adequately by a strain energy density function that depends only on 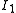 . For such materials we have
. For such materials we have 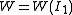 and
and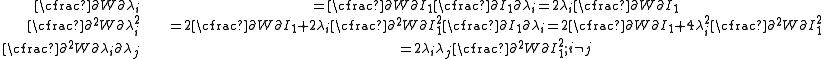
The consistency conditions for incompressible materials for
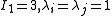 may then be expressed as
may then be expressed as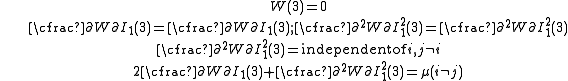
See also
- Cauchy elastic materialCauchy elastic materialA Cauchy-elastic material is one in which the Cauchy stress at each material point is determined only by the current state of deformation . A Cauchy-elastic material is one in which the Cauchy stress at each material point is determined only by the current state of deformation (with respect to an...
- Continuum mechanicsContinuum mechanicsContinuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
- Deformation (mechanics)Deformation (mechanics)Deformation in continuum mechanics is the transformation of a body from a reference configuration to a current configuration. A configuration is a set containing the positions of all particles of the body...
- Finite strain theory
- Rubber elasticityRubber ElasticityRubber elasticity, a well-known example of hyperelasticity, describes the mechanical behavior of many polymers, especially those with crosslinking. Invoking the theory of rubber elasticity, one considers a polymer chain in a crosslinked network as an entropic spring. When the chain is stretched,...
- Stress measuresStress measuresThe most commonly used measure of stress is the Cauchy stress. However, several other measures of stress can be defined. Some such stress measures that are widely used in continuum mechanics, particularly in the computational context, are:...
- Stress (mechanics)

