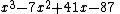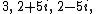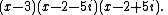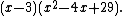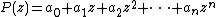Complex conjugate root theorem
Encyclopedia
In mathematics
, the complex conjugate root theorem states that if P is a polynomial
in one variable with real coefficients, and a + bi is a root of P with a and b real numbers, then its complex conjugate
a − bi is also a root of P.
It follows from this (and the fundamental theorem of algebra
), that if the degree of a real polynomial is odd, it must have at least one real root. That fact can also be proved by using the intermediate value theorem
.
that if the degree of a real polynomial is odd, it must have at least one real root.
This can be proved as follows.
This requires some care in the presence of multiple roots; but a complex root and its conjugate do have the same multiplicity (and this lemma
is not hard to prove). It can also be worked around by considering only irreducible polynomial
s; any real polynomial of odd degree must have an irreducible factor of odd degree, which (having no multiple roots) must have a real root by the reasoning above.
This corollary can also be proved directly by using the intermediate value theorem
.
Consider the polynomial
where all ar are real. Suppose some complex number ζ is a root of P, that is P(ζ) = 0. Then
which can be put as
Given the properties of complex conjugation,
Thus it follows that
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the complex conjugate root theorem states that if P is a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
in one variable with real coefficients, and a + bi is a root of P with a and b real numbers, then its complex conjugate
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
a − bi is also a root of P.
It follows from this (and the fundamental theorem of algebra
Fundamental theorem of algebra
The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
), that if the degree of a real polynomial is odd, it must have at least one real root. That fact can also be proved by using the intermediate value theorem
Intermediate value theorem
In mathematical analysis, the intermediate value theorem states that for each value between the least upper bound and greatest lower bound of the image of a continuous function there is at least one point in its domain that the function maps to that value....
.
Examples and consequences
- The polynomial x2 + 1 = 0 has roots ±i.
- Any real square matrix of odd degree has at least one real eigenvalue. For example, if the matrix is orthogonalOrthogonal matrixIn linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
, then 1 or −1 is an eigenvalue. - The polynomial
-
- has roots
- and thus can be factored as
- In computing the product of the last two factors, the imaginary parts cancel, and we get
- The non-real factors come in pairs which when multiplied give quadratic polynomials with real coefficients. Since every polynomial with complex coefficients can be factored into 1st-degree factors (that is one way of stating the fundamental theorem of algebraFundamental theorem of algebraThe fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
), it follows that every polynomial with real coefficients can be factored into factors of degree no higher than 2: just 1st-degree and quadratic factors.
Corollary on odd-degree polynomials
It follows from the present theorem and the fundamental theorem of algebraFundamental theorem of algebra
The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
that if the degree of a real polynomial is odd, it must have at least one real root.
This can be proved as follows.
- Since non-real complex roots come in conjugate pairs, there are an even number of them;
- But a polynomial of odd degree has an odd number of roots;
- Therefore some of them must be real.
This requires some care in the presence of multiple roots; but a complex root and its conjugate do have the same multiplicity (and this lemma
Lemma (mathematics)
In mathematics, a lemma is a proven proposition which is used as a stepping stone to a larger result rather than as a statement in-and-of itself...
is not hard to prove). It can also be worked around by considering only irreducible polynomial
Irreducible polynomial
In mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
s; any real polynomial of odd degree must have an irreducible factor of odd degree, which (having no multiple roots) must have a real root by the reasoning above.
This corollary can also be proved directly by using the intermediate value theorem
Intermediate value theorem
In mathematical analysis, the intermediate value theorem states that for each value between the least upper bound and greatest lower bound of the image of a continuous function there is at least one point in its domain that the function maps to that value....
.
Simple proof
One proof of the theorem is as follows:Consider the polynomial
where all ar are real. Suppose some complex number ζ is a root of P, that is P(ζ) = 0. Then
which can be put as
Given the properties of complex conjugation,
Thus it follows that