
Clifford analysis
Encyclopedia
Clifford analysis, using Clifford algebra
s named after William Kingdon Clifford
, is the study of Dirac operator
s, and Dirac type operators in analysis and geometry, together with their applications. Examples of Dirac type operators include, but are not limited to, the Hodge-Dirac operator,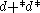 on a Riemannian manifold
on a Riemannian manifold
, the Dirac operator in euclidean space and its inverse on and their conformal equivalents on the sphere, the Laplacian in euclidean n-space and the Atiyah
and their conformal equivalents on the sphere, the Laplacian in euclidean n-space and the Atiyah
-Singer-Dirac operator on a spin manifold, Rarita-Schwinger/ Stein-Weiss type operators, conformal Laplacians, spinorial Laplacians and Dirac operators on Spinc manifolds, systems of Dirac operators, the Paneitz operator
, Dirac operators on hyperbolic space
, the hyperbolic Laplacian and Weinstein equations.
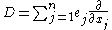
where e1...en is an orthonormal basis for Rn, and Rn is considered to be embedded in a complex Clifford algebra
, Cℓn(C) so that ej2 = -1.
This gives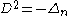
where Δn is the Laplacian in n-euclidean space.
The fundamental solution
to the euclidean Dirac operator is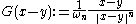
where ωn is the surface area of the unit sphere Sn-1.
Note that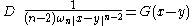
where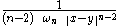 is the fundamental solution
is the fundamental solution
to Laplace's equation
for n ≥ 3.
The most basic example of a Dirac operator is the Cauchy-Riemann operator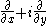 in the complex plane. Indeed many basic properties of one variable complex analysis
in the complex plane. Indeed many basic properties of one variable complex analysis
follow through for many first order Dirac type operators. In euclidean space this includes a Cauchy Theorem
, a Cauchy integral formula, Morera's Theorem
, Taylor series
, Laurent series
and Liouville Theorem
. In this case the Cauchy kernel is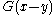 . The proof of the Cauchy integral formula is the same as in one complex variable and makes use of the fact that each non-zero vector
. The proof of the Cauchy integral formula is the same as in one complex variable and makes use of the fact that each non-zero vector  in euclidean space has a multiplicative inverse in the Clifford algebra, namely
in euclidean space has a multiplicative inverse in the Clifford algebra, namely 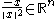 . Up to a sign this inverse is the Kelvin inverse of
. Up to a sign this inverse is the Kelvin inverse of  . Solutions to the euclidean Dirac equation
. Solutions to the euclidean Dirac equation 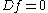 are called (left) monogenic functions. Monogenic functions are special cases of harmonic spinors on a spin manifold.
are called (left) monogenic functions. Monogenic functions are special cases of harmonic spinors on a spin manifold.
In 3 and 4 dimensions Clifford analysis is sometimes referred to as quaternion
ic analysis. When n=4 the Dirac operator is sometimes referred to as the Cauchy-Riemann-Fueter operator. Further some aspects of Clifford analysis are referred to as hypercomplex analysis.
Clifford analysis has analogues of Cauchy transforms, Bergman kernel
s, Szegő kernel
s, Plemelj operators, Hardy spaces, a Kerzman-Stein formula and a Π, or Beurling-Ahlfors, transform. These have all found applications in solving boundary value problem
s, including moving boundary value problems, singular integral
s and classic harmonic analysis. In particular Clifford analysis has been used to solve, in certain Sobolev space
s, the full water wave problem in 3-D. This method works in all dimensions greater than 2.
Much of Clifford analysis works if we replace the complex Clifford algebra
by a real Clifford algebra
,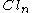 . This is not the case though when we need to deal with the interaction between the Dirac operator
. This is not the case though when we need to deal with the interaction between the Dirac operator
and the Fourier transform
.
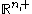 with boundary
with boundary 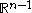 , the span of
, the span of 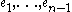 , under the Fourier transform
, under the Fourier transform
the symbol of the Dirac operator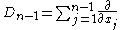 is
is 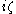 where
where 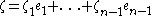 .
.
In this setting the Plemelj formulas are and the symbols for these operators are, up to a sign,
and the symbols for these operators are, up to a sign, 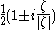 . These are projection operators, otherwise known as mutually annihilating idempotents, on the space of Cln(C) valued square integrable functions on Rn-1.
. These are projection operators, otherwise known as mutually annihilating idempotents, on the space of Cln(C) valued square integrable functions on Rn-1.
Note that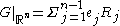 where
where 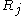 is the
is the 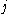 -th Riesz potential,
-th Riesz potential, 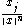 . As the symbol of
. As the symbol of 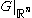 is
is 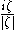 it is easily determined from the Clifford multiplication that
it is easily determined from the Clifford multiplication that 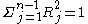 . So the convolution operator
. So the convolution operator 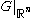 is a natural generalization to euclidean space of the Hilbert transform
is a natural generalization to euclidean space of the Hilbert transform
.
Suppose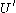 is a domain in
is a domain in  and
and 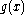 is a
is a  valued real analytic function. Then
valued real analytic function. Then 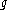 has a Cauchy-Kovalevskaia extension to the Dirac equation
has a Cauchy-Kovalevskaia extension to the Dirac equation
on some neighborhood of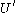 in
in 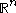 . The extension is explicitly given by
. The extension is explicitly given by 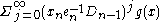 .
.
When this extension is applied to the variable in
in 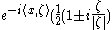 we get that
we get that 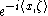 is the restriction to
is the restriction to  of
of 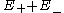 where
where 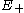 is a monogenic function in upper half space and
is a monogenic function in upper half space and 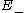 is a monogenic function in lower half space.
is a monogenic function in lower half space.
There is also a Paley-Weiner theorem in n-euclidean space arising in Clifford analysis.
or stereographic projection
from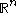 to the unit sphere
to the unit sphere 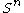 transforms the euclidean Dirac operator to a spherical Dirac operator
transforms the euclidean Dirac operator to a spherical Dirac operator 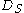 . Explicitly
. Explicitly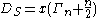
where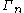 is the spherical Beltrami-Dirac operator
is the spherical Beltrami-Dirac operator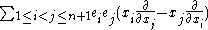
and .
.
The Cayley transform
over n-space is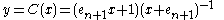
where . Its inverse is
. Its inverse is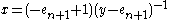 .
.
For a function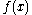 defined on a domain
defined on a domain 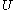 in n-euclidean space and a solution to the Dirac equation
in n-euclidean space and a solution to the Dirac equation
, then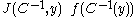 is annihilated by
is annihilated by  , on
, on 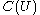 where
where 
Further , the conformal Laplacian or Yamabe operator on
, the conformal Laplacian or Yamabe operator on 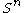 . Explicitly
. Explicitly 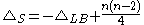 where
where 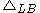 is the Laplace-Beltrami operator
is the Laplace-Beltrami operator
on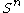 . The operator
. The operator  is, via the Cayley transform, conformally equivalent to the euclidean Laplacian. Also
is, via the Cayley transform, conformally equivalent to the euclidean Laplacian. Also 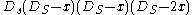 is the Paneitz operator,
is the Paneitz operator, 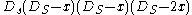 , on the n-sphere. Via the Cayley transform this operator is conformally equivalent to the bi-Laplacian,
, on the n-sphere. Via the Cayley transform this operator is conformally equivalent to the bi-Laplacian, 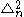 . These are all examples of operators of Dirac type.
. These are all examples of operators of Dirac type.
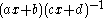 where
where  ,
, 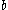 ,
,  and
and  ∈ Cln and satisfy certain constraints. The associated 2 × 2 matrix is called an Ahlfors-Vahlen matrix. If
∈ Cln and satisfy certain constraints. The associated 2 × 2 matrix is called an Ahlfors-Vahlen matrix. If 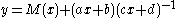 and
and 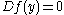 then
then 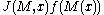 is a solution to the Dirac equation where
is a solution to the Dirac equation where 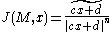 and
and 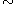 is a basic antiautomorphism acting on the Clifford algebra
is a basic antiautomorphism acting on the Clifford algebra
. The operators , or Δnk/2 when
, or Δnk/2 when 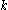 is even, exhibit similar covariances under Moebius transform including the Cayley transform
is even, exhibit similar covariances under Moebius transform including the Cayley transform
.
When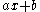 and
and 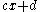 are non-zero they are both members of the Clifford group.
are non-zero they are both members of the Clifford group.
As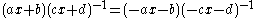 then we have a choice in sign in defining
then we have a choice in sign in defining 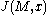 . This means that for a conformally flat manifold
. This means that for a conformally flat manifold 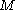 we need a spin structure
we need a spin structure
on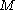 in order to define a spinor bundle on whose sections we can allow a Dirac operator to act. Explicit simple examples include the n-cylinder, the Hopf manifold obtained from n-euclidean space minus the origin, and generalizations of k-handled toruses obtained from upper half space by factoring it out by actions of generalized modular groups acting on upper half space totally discontinuosly. A Dirac operator
in order to define a spinor bundle on whose sections we can allow a Dirac operator to act. Explicit simple examples include the n-cylinder, the Hopf manifold obtained from n-euclidean space minus the origin, and generalizations of k-handled toruses obtained from upper half space by factoring it out by actions of generalized modular groups acting on upper half space totally discontinuosly. A Dirac operator
can be introduced in these contexts. These Dirac operators are special examples of Atiyah-Singer-Dirac operators.
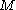 , with a spinor bundle
, with a spinor bundle 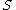 then given a smooth section
then given a smooth section 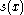 in
in 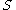 then in terms of a local orthonormal basis e1(x)... en(x) of the tangent bundle of
then in terms of a local orthonormal basis e1(x)... en(x) of the tangent bundle of 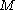 the Atiyah-Singer-Dirac operator acting on
the Atiyah-Singer-Dirac operator acting on  is defined to be
is defined to be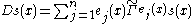
where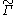 is the lifting to
is the lifting to 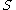 of the Levi-Civita connection
of the Levi-Civita connection
on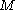 . When
. When 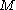 is n-euclidean space we return to the euclidean Dirac operator
is n-euclidean space we return to the euclidean Dirac operator
.
From an Atiyah-Singer-Dirac operator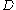 we have the Lichnerowicz formula
we have the Lichnerowicz formula
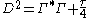
where is the scalar curvature on the manifold
is the scalar curvature on the manifold
, and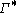 is the adjoint of
is the adjoint of 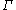 . The operator
. The operator 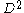 is known as the spinorial Laplacian.
is known as the spinorial Laplacian.
If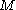 is compact and
is compact and 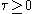 and
and 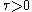 somewhere then there are no non-trivial harmonic spinors on the manifold. This is Lichnerowicz' Theorem. It is readily seen that that Lichnerowicz' Theorem is a generalization of Liouville's Theorem from one variable complex analysis. This allows us to note that over the space of smooth spinor sections
somewhere then there are no non-trivial harmonic spinors on the manifold. This is Lichnerowicz' Theorem. It is readily seen that that Lichnerowicz' Theorem is a generalization of Liouville's Theorem from one variable complex analysis. This allows us to note that over the space of smooth spinor sections
the operator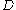 is invertible for such a manifold.
is invertible for such a manifold.
In the cases where the Atiyah-Singer-Dirac operator is invertible on the space of smooth spinor sections with compact support one may introduce
where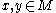 with
with 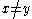 and
and 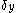 is the Dirac delta function
is the Dirac delta function
evaluated at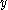 . This gives rise to a Cauchy kernel, which is the fundamental solution
. This gives rise to a Cauchy kernel, which is the fundamental solution
to this Dirac operator. From this one may obtain a Cauchy integral formula for harmonic spinors. With this kernel much of what is described in the first section of this entry carries through for invertible Atiyah-Singer-Dirac operators.
Using Stokes' theorem
, or otherwise, one can further determine that under a conformal change of metric the Dirac operators associated to each metric are proportional to each other, and consequently so are their inverses, if they exist.
All of this provides potential links to Atiyah-Singer index theory and other aspects of geometric analysis involving Dirac type operators.
metric.
For upper half space one splits the Clifford algebra
,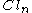 into
into 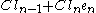 . So for
. So for 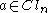 one may express
one may express  as
as 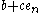 with
with  ,
, 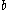
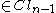 . One then has projection operators
. One then has projection operators 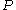 and
and  defined as follows
defined as follows 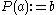 and
and 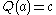 . The Hodge-Dirac operator acting on a function
. The Hodge-Dirac operator acting on a function 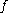 with respect to the hyperbolic metric in upper half space is now defined to be
with respect to the hyperbolic metric in upper half space is now defined to be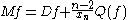 .
.
In this case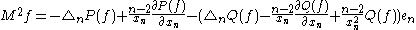 .
.
The operator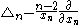 is the Laplacian with respect to the Poincaré metric
is the Laplacian with respect to the Poincaré metric
while the other operator is an example of a Weinstein operator.
The hyperbolic Laplacian is invariant under actions of the conformal group, while the hyperbolic Dirac operator is covariant under such actions.
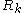 is a conformally covariant first order differential operator. Here
is a conformally covariant first order differential operator. Here  . When
. When 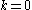 then the Rarita-Schwinger operator is just the Dirac operator. In representation theory for the orthogonal group,
then the Rarita-Schwinger operator is just the Dirac operator. In representation theory for the orthogonal group, 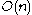 it is common to consider functions taking values in spaces of homogeneous harmonic
it is common to consider functions taking values in spaces of homogeneous harmonic
polynomials. When one refines this representation theory to the double covering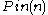 of
of 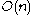 one replaces spaces of homogeneous harmonic polynomials by spaces of k homogeneous polynomial solutions to the Dirac equation, otherwise known as
one replaces spaces of homogeneous harmonic polynomials by spaces of k homogeneous polynomial solutions to the Dirac equation, otherwise known as 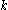 monogenic polynomials. One considers a function
monogenic polynomials. One considers a function 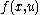 where
where 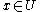 a domain in
a domain in 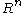 and
and  varies over
varies over 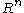 . Further
. Further 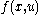 is a k-monogenic polynomial in
is a k-monogenic polynomial in  . Now apply the Dirac operator
. Now apply the Dirac operator 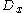 in
in  to
to 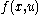 . Now as the Clifford algebra is not commutative
. Now as the Clifford algebra is not commutative 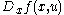 then this function is no longer
then this function is no longer 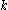 monogenic but is a homogeneous harmonic polynomial in
monogenic but is a homogeneous harmonic polynomial in  . Now for each harmonic polynomial
. Now for each harmonic polynomial  homogeneous of degree
homogeneous of degree 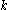 there is an Almansi-Fischer decomposition
there is an Almansi-Fischer decomposition  where
where 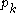 and
and  are respectively
are respectively 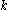 and
and 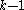 monogenic polynomials. Let
monogenic polynomials. Let 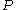 be the projection of
be the projection of 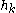 to
to 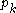 then the Rarita Schwinger operator is defined to be
then the Rarita Schwinger operator is defined to be 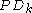 , and it is denoted by
, and it is denoted by 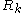 . Using Euler's Lemma one may determine that
. Using Euler's Lemma one may determine that  . So
. So  .
.
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
s named after William Kingdon Clifford
William Kingdon Clifford
William Kingdon Clifford FRS was an English mathematician and philosopher. Building on the work of Hermann Grassmann, he introduced what is now termed geometric algebra, a special case of the Clifford algebra named in his honour, with interesting applications in contemporary mathematical physics...
, is the study of Dirac operator
Dirac operator
In mathematics and quantum mechanics, a Dirac operator is a differential operator that is a formal square root, or half-iterate, of a second-order operator such as a Laplacian...
s, and Dirac type operators in analysis and geometry, together with their applications. Examples of Dirac type operators include, but are not limited to, the Hodge-Dirac operator,
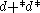 on a Riemannian manifold
on a Riemannian manifoldRiemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
, the Dirac operator in euclidean space and its inverse on
 and their conformal equivalents on the sphere, the Laplacian in euclidean n-space and the Atiyah
and their conformal equivalents on the sphere, the Laplacian in euclidean n-space and the AtiyahAtiyah
Atiyah is the surname of several notable people including:*Sir Michael Atiyah, British mathematician, brother of Patrick*Patrick Atiyah, English barrister and legal writer, brother of Michael*Edward Atiyah, Lebanese born writer, father of Michael and Patrick...
-Singer-Dirac operator on a spin manifold, Rarita-Schwinger/ Stein-Weiss type operators, conformal Laplacians, spinorial Laplacians and Dirac operators on Spinc manifolds, systems of Dirac operators, the Paneitz operator
Paneitz operator
In the mathematical field of differential geometry, the Paneitz operator is a fourth-order differential operator defined on a Riemannian manifold of dimension n. It is named after Stephen Paneitz, who discovered it in 1983, and whose preprint was later published posthumously in...
, Dirac operators on hyperbolic space
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
, the hyperbolic Laplacian and Weinstein equations.
Euclidean space
In Euclidean space the Dirac operator has the form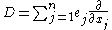
where e1...en is an orthonormal basis for Rn, and Rn is considered to be embedded in a complex Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
, Cℓn(C) so that ej2 = -1.
This gives
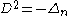
where Δn is the Laplacian in n-euclidean space.
The fundamental solution
Fundamental solution
In mathematics, a fundamental solution for a linear partial differential operator L is a formulation in the language of distribution theory of the older idea of a Green's function...
to the euclidean Dirac operator is
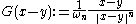
where ωn is the surface area of the unit sphere Sn-1.
Note that
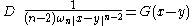
where
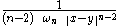 is the fundamental solution
is the fundamental solutionFundamental solution
In mathematics, a fundamental solution for a linear partial differential operator L is a formulation in the language of distribution theory of the older idea of a Green's function...
to Laplace's equation
Laplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
for n ≥ 3.
The most basic example of a Dirac operator is the Cauchy-Riemann operator
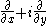 in the complex plane. Indeed many basic properties of one variable complex analysis
in the complex plane. Indeed many basic properties of one variable complex analysisComplex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
follow through for many first order Dirac type operators. In euclidean space this includes a Cauchy Theorem
Cauchy theorem
Several theorems are named after Augustin-Louis Cauchy. Cauchy theorem may mean:*Cauchy's integral theorem in complex analysis, also Cauchy's integral formula*Cauchy's mean value theorem in real analysis, an extended form of the mean value theorem...
, a Cauchy integral formula, Morera's Theorem
Morera's theorem
In complex analysis, a branch of mathematics, Morera's theorem, named after Giacinto Morera, gives an important criterion for proving that a function is holomorphic....
, Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
, Laurent series
Laurent series
In mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...
and Liouville Theorem
Liouville's theorem (complex analysis)
In complex analysis, Liouville's theorem, named after Joseph Liouville, states that every bounded entire function must be constant. That is, every holomorphic function f for which there exists a positive number M such that |f| ≤ M for all z in C is constant.The theorem is considerably improved by...
. In this case the Cauchy kernel is
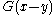 . The proof of the Cauchy integral formula is the same as in one complex variable and makes use of the fact that each non-zero vector
. The proof of the Cauchy integral formula is the same as in one complex variable and makes use of the fact that each non-zero vector  in euclidean space has a multiplicative inverse in the Clifford algebra, namely
in euclidean space has a multiplicative inverse in the Clifford algebra, namely 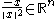 . Up to a sign this inverse is the Kelvin inverse of
. Up to a sign this inverse is the Kelvin inverse of  . Solutions to the euclidean Dirac equation
. Solutions to the euclidean Dirac equation 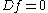 are called (left) monogenic functions. Monogenic functions are special cases of harmonic spinors on a spin manifold.
are called (left) monogenic functions. Monogenic functions are special cases of harmonic spinors on a spin manifold.In 3 and 4 dimensions Clifford analysis is sometimes referred to as quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
ic analysis. When n=4 the Dirac operator is sometimes referred to as the Cauchy-Riemann-Fueter operator. Further some aspects of Clifford analysis are referred to as hypercomplex analysis.
Clifford analysis has analogues of Cauchy transforms, Bergman kernel
Bergman kernel
In the mathematical study of several complex variables, the Bergman kernel, named after Stefan Bergman, is a reproducing kernel for the Hilbert space of all square integrable holomorphic functions on a domain D in Cn....
s, Szegő kernel
Szegő kernel
In the mathematical study of several complex variables, the Szegő kernel is an integral kernel that gives rise to a reproducing kernel on a natural Hilbert space of holomorphic functions...
s, Plemelj operators, Hardy spaces, a Kerzman-Stein formula and a Π, or Beurling-Ahlfors, transform. These have all found applications in solving boundary value problem
Boundary value problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
s, including moving boundary value problems, singular integral
Singular integral
In mathematics, singular integrals are central to harmonic analysis and are intimately connected with the study of partial differential equations. Broadly speaking a singular integral is an integral operator...
s and classic harmonic analysis. In particular Clifford analysis has been used to solve, in certain Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
s, the full water wave problem in 3-D. This method works in all dimensions greater than 2.
Much of Clifford analysis works if we replace the complex Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
by a real Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
,
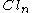 . This is not the case though when we need to deal with the interaction between the Dirac operator
. This is not the case though when we need to deal with the interaction between the Dirac operatorDirac operator
In mathematics and quantum mechanics, a Dirac operator is a differential operator that is a formal square root, or half-iterate, of a second-order operator such as a Laplacian...
and the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
.
The Fourier Transform
When we consider upper half space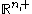 with boundary
with boundary 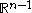 , the span of
, the span of 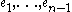 , under the Fourier transform
, under the Fourier transformFourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
the symbol of the Dirac operator
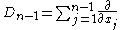 is
is 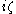 where
where 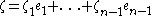 .
.In this setting the Plemelj formulas are
 and the symbols for these operators are, up to a sign,
and the symbols for these operators are, up to a sign, 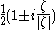 . These are projection operators, otherwise known as mutually annihilating idempotents, on the space of Cln(C) valued square integrable functions on Rn-1.
. These are projection operators, otherwise known as mutually annihilating idempotents, on the space of Cln(C) valued square integrable functions on Rn-1.Note that
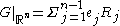 where
where 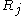 is the
is the 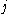 -th Riesz potential,
-th Riesz potential, 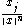 . As the symbol of
. As the symbol of 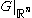 is
is 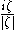 it is easily determined from the Clifford multiplication that
it is easily determined from the Clifford multiplication that 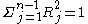 . So the convolution operator
. So the convolution operator 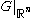 is a natural generalization to euclidean space of the Hilbert transform
is a natural generalization to euclidean space of the Hilbert transformHilbert transform
In mathematics and in signal processing, the Hilbert transform is a linear operator which takes a function, u, and produces a function, H, with the same domain. The Hilbert transform is named after David Hilbert, who first introduced the operator in order to solve a special case of the...
.
Suppose
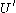 is a domain in
is a domain in  and
and 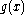 is a
is a  valued real analytic function. Then
valued real analytic function. Then 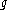 has a Cauchy-Kovalevskaia extension to the Dirac equation
has a Cauchy-Kovalevskaia extension to the Dirac equationDirac equation
The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
on some neighborhood of
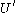 in
in 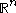 . The extension is explicitly given by
. The extension is explicitly given by 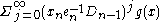 .
.When this extension is applied to the variable
 in
in 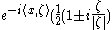 we get that
we get that 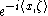 is the restriction to
is the restriction to  of
of 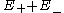 where
where 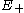 is a monogenic function in upper half space and
is a monogenic function in upper half space and 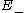 is a monogenic function in lower half space.
is a monogenic function in lower half space.There is also a Paley-Weiner theorem in n-euclidean space arising in Clifford analysis.
Conformal Structure
Many Dirac type operators have a covariance under conformal change in metric. This is true for the Dirac operator in euclidean space, and the Dirac operator on the sphere under Moebius transformations. Consequently this holds true for Dirac operators on conformally flat manifolds and conformal manifolds which are simultaneously spin manifolds.Cayley transform (stereographic projection)
The Cayley transformCayley transform
In mathematics, the Cayley transform, named after Arthur Cayley, has a cluster of related meanings. As originally described by , the Cayley transform is a mapping between skew-symmetric matrices and special orthogonal matrices. In complex analysis, the Cayley transform is a conformal mapping in...
or stereographic projection
Stereographic projection
The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...
from
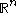 to the unit sphere
to the unit sphere 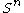 transforms the euclidean Dirac operator to a spherical Dirac operator
transforms the euclidean Dirac operator to a spherical Dirac operator 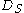 . Explicitly
. Explicitly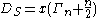
where
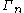 is the spherical Beltrami-Dirac operator
is the spherical Beltrami-Dirac operator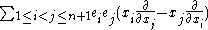
and
 .
.The Cayley transform
Cayley transform
In mathematics, the Cayley transform, named after Arthur Cayley, has a cluster of related meanings. As originally described by , the Cayley transform is a mapping between skew-symmetric matrices and special orthogonal matrices. In complex analysis, the Cayley transform is a conformal mapping in...
over n-space is
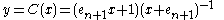
where
 . Its inverse is
. Its inverse is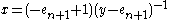 .
.For a function
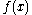 defined on a domain
defined on a domain 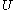 in n-euclidean space and a solution to the Dirac equation
in n-euclidean space and a solution to the Dirac equationDirac equation
The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
, then
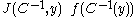 is annihilated by
is annihilated by  , on
, on 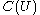 where
where 
Further
 , the conformal Laplacian or Yamabe operator on
, the conformal Laplacian or Yamabe operator on 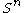 . Explicitly
. Explicitly 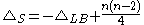 where
where 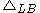 is the Laplace-Beltrami operator
is the Laplace-Beltrami operatorLaplace-Beltrami operator
In differential geometry, the Laplace operator, named after Pierre-Simon Laplace, can be generalized to operate on functions defined on surfaces in Euclidean space and, more generally, on Riemannian and pseudo-Riemannian manifolds. This more general operator goes by the name Laplace–Beltrami...
on
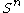 . The operator
. The operator  is, via the Cayley transform, conformally equivalent to the euclidean Laplacian. Also
is, via the Cayley transform, conformally equivalent to the euclidean Laplacian. Also 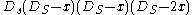 is the Paneitz operator,
is the Paneitz operator, 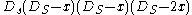 , on the n-sphere. Via the Cayley transform this operator is conformally equivalent to the bi-Laplacian,
, on the n-sphere. Via the Cayley transform this operator is conformally equivalent to the bi-Laplacian, 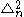 . These are all examples of operators of Dirac type.
. These are all examples of operators of Dirac type.Moebius transform
A Moebius transform over n-euclidean space can be expressed as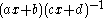 where
where  ,
, 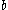 ,
,  and
and  ∈ Cln and satisfy certain constraints. The associated 2 × 2 matrix is called an Ahlfors-Vahlen matrix. If
∈ Cln and satisfy certain constraints. The associated 2 × 2 matrix is called an Ahlfors-Vahlen matrix. If 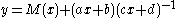 and
and 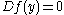 then
then 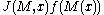 is a solution to the Dirac equation where
is a solution to the Dirac equation where 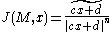 and
and 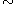 is a basic antiautomorphism acting on the Clifford algebra
is a basic antiautomorphism acting on the Clifford algebraClifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
. The operators
 , or Δnk/2 when
, or Δnk/2 when 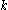 is even, exhibit similar covariances under Moebius transform including the Cayley transform
is even, exhibit similar covariances under Moebius transform including the Cayley transformCayley transform
In mathematics, the Cayley transform, named after Arthur Cayley, has a cluster of related meanings. As originally described by , the Cayley transform is a mapping between skew-symmetric matrices and special orthogonal matrices. In complex analysis, the Cayley transform is a conformal mapping in...
.
When
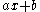 and
and 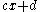 are non-zero they are both members of the Clifford group.
are non-zero they are both members of the Clifford group.As
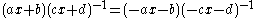 then we have a choice in sign in defining
then we have a choice in sign in defining 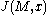 . This means that for a conformally flat manifold
. This means that for a conformally flat manifold 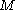 we need a spin structure
we need a spin structureSpin structure
In differential geometry, a spin structure on an orientable Riemannian manifold \,allows one to define associated spinor bundles, giving rise to the notion of a spinor in differential geometry....
on
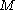 in order to define a spinor bundle on whose sections we can allow a Dirac operator to act. Explicit simple examples include the n-cylinder, the Hopf manifold obtained from n-euclidean space minus the origin, and generalizations of k-handled toruses obtained from upper half space by factoring it out by actions of generalized modular groups acting on upper half space totally discontinuosly. A Dirac operator
in order to define a spinor bundle on whose sections we can allow a Dirac operator to act. Explicit simple examples include the n-cylinder, the Hopf manifold obtained from n-euclidean space minus the origin, and generalizations of k-handled toruses obtained from upper half space by factoring it out by actions of generalized modular groups acting on upper half space totally discontinuosly. A Dirac operatorDirac operator
In mathematics and quantum mechanics, a Dirac operator is a differential operator that is a formal square root, or half-iterate, of a second-order operator such as a Laplacian...
can be introduced in these contexts. These Dirac operators are special examples of Atiyah-Singer-Dirac operators.
The Atiyah-Singer-Dirac Operator
Given a spin manifold,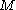 , with a spinor bundle
, with a spinor bundle 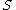 then given a smooth section
then given a smooth section 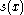 in
in 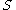 then in terms of a local orthonormal basis e1(x)... en(x) of the tangent bundle of
then in terms of a local orthonormal basis e1(x)... en(x) of the tangent bundle of 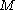 the Atiyah-Singer-Dirac operator acting on
the Atiyah-Singer-Dirac operator acting on  is defined to be
is defined to be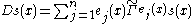
where
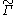 is the lifting to
is the lifting to 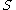 of the Levi-Civita connection
of the Levi-Civita connectionLevi-Civita connection
In Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
on
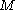 . When
. When 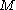 is n-euclidean space we return to the euclidean Dirac operator
is n-euclidean space we return to the euclidean Dirac operatorDirac operator
In mathematics and quantum mechanics, a Dirac operator is a differential operator that is a formal square root, or half-iterate, of a second-order operator such as a Laplacian...
.
From an Atiyah-Singer-Dirac operator
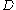 we have the Lichnerowicz formula
we have the Lichnerowicz formulaLichnerowicz formula
The Lichnerowicz formula is a fundamental equation in the analysis of spinors on pseudo-Riemannian manifolds. In dimension 4, it forms a piece of Seiberg–Witten theory and other aspects of gauge theory. It is named after noted mathematician André Lichnerowicz who proved it in 1963...
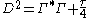
where
 is the scalar curvature on the manifold
is the scalar curvature on the manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
, and
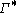 is the adjoint of
is the adjoint of 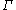 . The operator
. The operator 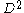 is known as the spinorial Laplacian.
is known as the spinorial Laplacian.If
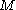 is compact and
is compact and 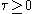 and
and 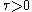 somewhere then there are no non-trivial harmonic spinors on the manifold. This is Lichnerowicz' Theorem. It is readily seen that that Lichnerowicz' Theorem is a generalization of Liouville's Theorem from one variable complex analysis. This allows us to note that over the space of smooth spinor sections
somewhere then there are no non-trivial harmonic spinors on the manifold. This is Lichnerowicz' Theorem. It is readily seen that that Lichnerowicz' Theorem is a generalization of Liouville's Theorem from one variable complex analysis. This allows us to note that over the space of smooth spinor sectionsthe operator
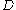 is invertible for such a manifold.
is invertible for such a manifold.In the cases where the Atiyah-Singer-Dirac operator is invertible on the space of smooth spinor sections with compact support one may introduce

where
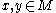 with
with 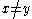 and
and 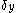 is the Dirac delta function
is the Dirac delta functionDirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
evaluated at
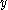 . This gives rise to a Cauchy kernel, which is the fundamental solution
. This gives rise to a Cauchy kernel, which is the fundamental solutionFundamental solution
In mathematics, a fundamental solution for a linear partial differential operator L is a formulation in the language of distribution theory of the older idea of a Green's function...
to this Dirac operator. From this one may obtain a Cauchy integral formula for harmonic spinors. With this kernel much of what is described in the first section of this entry carries through for invertible Atiyah-Singer-Dirac operators.
Using Stokes' theorem
Stokes' theorem
In differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
, or otherwise, one can further determine that under a conformal change of metric the Dirac operators associated to each metric are proportional to each other, and consequently so are their inverses, if they exist.
All of this provides potential links to Atiyah-Singer index theory and other aspects of geometric analysis involving Dirac type operators.
Hyperbolic Dirac Type Operators
In Clifford analysis one also considers differential operators on upper half space, the disc, or hyperbola with respect to the hyperbolic, or PoincaréPoincaré
Several members of the French Poincaré family have been successful in public and scientific life:* Henri Poincaré , physicist, mathematician and philosopher of science* Lucien Poincaré , physicist, brother of Raymond and cousin of Henri...
metric.
For upper half space one splits the Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
,
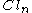 into
into 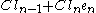 . So for
. So for 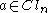 one may express
one may express  as
as 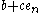 with
with  ,
, 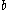
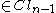 . One then has projection operators
. One then has projection operators 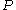 and
and  defined as follows
defined as follows 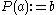 and
and 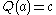 . The Hodge-Dirac operator acting on a function
. The Hodge-Dirac operator acting on a function 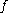 with respect to the hyperbolic metric in upper half space is now defined to be
with respect to the hyperbolic metric in upper half space is now defined to be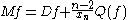 .
.In this case
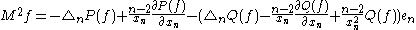 .
.The operator
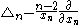 is the Laplacian with respect to the Poincaré metric
is the Laplacian with respect to the Poincaré metricPoincaré metric
In mathematics, the Poincaré metric, named after Henri Poincaré, is the metric tensor describing a two-dimensional surface of constant negative curvature. It is the natural metric commonly used in a variety of calculations in hyperbolic geometry or Riemann surfaces.There are three equivalent...
while the other operator is an example of a Weinstein operator.
The hyperbolic Laplacian is invariant under actions of the conformal group, while the hyperbolic Dirac operator is covariant under such actions.
Rarita-Schwinger/ Stein-Weiss Operators
Rarita-Schwinger operators, also known as Stein-Weiss operators, arise in representation theory for the Spin and Pin groups. The operator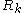 is a conformally covariant first order differential operator. Here
is a conformally covariant first order differential operator. Here  . When
. When 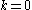 then the Rarita-Schwinger operator is just the Dirac operator. In representation theory for the orthogonal group,
then the Rarita-Schwinger operator is just the Dirac operator. In representation theory for the orthogonal group, 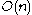 it is common to consider functions taking values in spaces of homogeneous harmonic
it is common to consider functions taking values in spaces of homogeneous harmonicpolynomials. When one refines this representation theory to the double covering
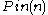 of
of 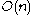 one replaces spaces of homogeneous harmonic polynomials by spaces of k homogeneous polynomial solutions to the Dirac equation, otherwise known as
one replaces spaces of homogeneous harmonic polynomials by spaces of k homogeneous polynomial solutions to the Dirac equation, otherwise known as 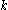 monogenic polynomials. One considers a function
monogenic polynomials. One considers a function 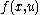 where
where 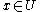 a domain in
a domain in 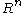 and
and  varies over
varies over 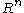 . Further
. Further 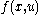 is a k-monogenic polynomial in
is a k-monogenic polynomial in  . Now apply the Dirac operator
. Now apply the Dirac operator 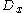 in
in  to
to 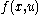 . Now as the Clifford algebra is not commutative
. Now as the Clifford algebra is not commutative 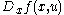 then this function is no longer
then this function is no longer 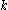 monogenic but is a homogeneous harmonic polynomial in
monogenic but is a homogeneous harmonic polynomial in  . Now for each harmonic polynomial
. Now for each harmonic polynomial  homogeneous of degree
homogeneous of degree 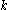 there is an Almansi-Fischer decomposition
there is an Almansi-Fischer decomposition  where
where 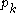 and
and  are respectively
are respectively 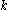 and
and 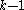 monogenic polynomials. Let
monogenic polynomials. Let 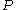 be the projection of
be the projection of 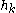 to
to 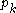 then the Rarita Schwinger operator is defined to be
then the Rarita Schwinger operator is defined to be 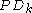 , and it is denoted by
, and it is denoted by 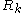 . Using Euler's Lemma one may determine that
. Using Euler's Lemma one may determine that  . So
. So  .
.See also
- Clifford algebraClifford algebraIn mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
- Complex spin structure
- Conformal manifold
- Conformally flat manifold
- Dirac operatorDirac operatorIn mathematics and quantum mechanics, a Dirac operator is a differential operator that is a formal square root, or half-iterate, of a second-order operator such as a Laplacian...
- Poincaré metricPoincaré metricIn mathematics, the Poincaré metric, named after Henri Poincaré, is the metric tensor describing a two-dimensional surface of constant negative curvature. It is the natural metric commonly used in a variety of calculations in hyperbolic geometry or Riemann surfaces.There are three equivalent...
- Spin structureSpin structureIn differential geometry, a spin structure on an orientable Riemannian manifold \,allows one to define associated spinor bundles, giving rise to the notion of a spinor in differential geometry....
- Spinor bundle

