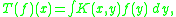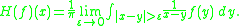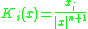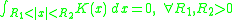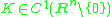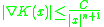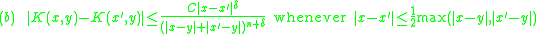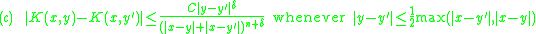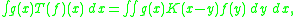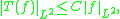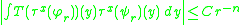Singular integral
Encyclopedia
In mathematics
, singular integrals are central to harmonic analysis
and are intimately connected with the study of partial differential equations. Broadly speaking a singular integral is an integral operator
whose kernel function K : Rn×Rn → Rn is singular
along the diagonal x = y. Specifically, the singularity is such that |K(x, y)| is of size |x − y|−n asymptotically as |x − y| → 0. Since such integrals may not in general be absolutely integrable, a rigorous definition must define them as the limit of the integral over |y − x| > ε as ε → 0, but in practice this is a technicality. Usually further assumptions are required to obtain results such as their boundedness on Lp(Rn).
H. It is given by convolution against the kernel K(x) = 1/(πx) for x in R. More precisely,
The most straightforward higher dimension analogues of these are the Riesz transforms, which replace K(x) = 1/x with
where i = 1, …, n and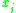
is the i-th component of x in Rn. All of these operators are bounded on Lp and satisfy weak-type (1, 1) estimates.
on Rn\{0}, in the sense that
Suppose that the kernel satisfies:
1. The size condition on the Fourier transform
of K
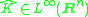
2. The smoothness condition: for some C > 0,
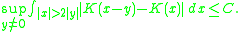
Then it can be shown that T is bounded on Lp(Rn) and satisfies a weak-type (1, 1) estimate.
Property 1. is needed to ensure that convolution with the tempered distribution
p.v. K given by the principal value integral
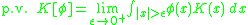
is a well-defined Fourier multiplier on L2. Neither of the properties 1. or 2. is necessarily easy to verify, and a variety of sufficient conditions exist. Typically in applications, one also has a cancellation condition
which is quite easy to check. It is automatic, for instance, if K is an odd function. If, in addition, one assumes 2. and the following size condition
then it can be shown that 1. follows.
The smoothness condition 2. is also often difficult to check in principle, the following sufficient condition of a kernel K can be used:
Observe that these conditions are satisfied for the Hilbert and Riesz transforms, so this result is an extension of those result.
–Zygmund
kernel if it satisfies the following conditions for some constants C > 0 and δ > 0.
whenever f and g are smooth and have disjoint support. Such operators need not be bounded on Lp
for all smooth compactly supported ƒ.
It can be proved that such operators are, in fact, also bounded on all Lp with 1 < p < ∞.
A normalised bump is a smooth function φ on Rn supported in a ball of radius 10 and centred at the origin such that |∂α φ(x)| ≤ 1, for all multi-indices |α| ≤ n + 2. Denote by τx(φ)(y) = φ(y − x) and φr(x) = r−nφ(x/r) for all x in Rn and r > 0. An operator is said to be weakly bounded if there is a constant C such that
for all normalised bumps φ and ψ. A function is said to be accretive if there is a constant c > 0 such that Re(b)(x) ≥ c for all x in R. Denote by Mb the operator given by multiplication by a function b.
The T(b) theorem states that a singular integral operator T associated to a Calderón–Zygmund kernel is bounded on L2 if it satisfies all of the following three conditions for some bounded accretive functions b1 and b2:
(a)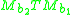
is weakly bounded;
(b)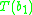
is in BMO
;
(c)
is in BMO
, where Tt is the transpose operator of T.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, singular integrals are central to harmonic analysis
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
and are intimately connected with the study of partial differential equations. Broadly speaking a singular integral is an integral operator
whose kernel function K : Rn×Rn → Rn is singular
Mathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
along the diagonal x = y. Specifically, the singularity is such that |K(x, y)| is of size |x − y|−n asymptotically as |x − y| → 0. Since such integrals may not in general be absolutely integrable, a rigorous definition must define them as the limit of the integral over |y − x| > ε as ε → 0, but in practice this is a technicality. Usually further assumptions are required to obtain results such as their boundedness on Lp(Rn).
The Hilbert transform
The archetypal singular integral operator is the Hilbert transformHilbert transform
In mathematics and in signal processing, the Hilbert transform is a linear operator which takes a function, u, and produces a function, H, with the same domain. The Hilbert transform is named after David Hilbert, who first introduced the operator in order to solve a special case of the...
H. It is given by convolution against the kernel K(x) = 1/(πx) for x in R. More precisely,
The most straightforward higher dimension analogues of these are the Riesz transforms, which replace K(x) = 1/x with
where i = 1, …, n and
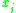is the i-th component of x in Rn. All of these operators are bounded on Lp and satisfy weak-type (1, 1) estimates.Singular integrals of convolution type
A singular integral of convolution type is an operator T defined by convolution with a kernel K that is locally integrableLocally integrable function
In mathematics, a locally integrable function is a function which is integrable on any compact set of its domain of definition. Their importance lies on the fact that we do not care about their behavior at infinity.- Formal definition :...
on Rn\{0}, in the sense that
Suppose that the kernel satisfies:
1. The size condition on the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of K
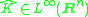
2. The smoothness condition: for some C > 0,
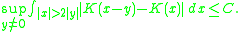
Then it can be shown that T is bounded on Lp(Rn) and satisfies a weak-type (1, 1) estimate.
Property 1. is needed to ensure that convolution with the tempered distribution
Tempered distribution
*Distribution *Tempered representation...
p.v. K given by the principal value integral
Cauchy principal value
In mathematics, the Cauchy principal value, named after Augustin Louis Cauchy, is a method for assigning values to certain improper integrals which would otherwise be undefined.-Formulation:...
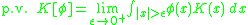
is a well-defined Fourier multiplier on L2. Neither of the properties 1. or 2. is necessarily easy to verify, and a variety of sufficient conditions exist. Typically in applications, one also has a cancellation condition
which is quite easy to check. It is automatic, for instance, if K is an odd function. If, in addition, one assumes 2. and the following size condition
then it can be shown that 1. follows.
The smoothness condition 2. is also often difficult to check in principle, the following sufficient condition of a kernel K can be used:
Observe that these conditions are satisfied for the Hilbert and Riesz transforms, so this result is an extension of those result.
Singular integrals of non-convolution type
These are even more general operators. However, since our assumptions are so weak, it is not necessarily the case that these operators are bounded on L'p.Calderón–Zygmund kernels
A function K : Rn×Rn → R is said to be a CalderónAlberto Calderón
Alberto Pedro Calderón was an Argentine mathematician best known for his work on the theory of partial differential equations and singular integral operators, and widely considered as one of the 20th century's most important mathematicians...
–Zygmund
Antoni Zygmund
Antoni Zygmund was a Polish-born American mathematician.-Life:Born in Warsaw, Zygmund obtained his PhD from Warsaw University and became a professor at Stefan Batory University at Wilno...
kernel if it satisfies the following conditions for some constants C > 0 and δ > 0.
Singular integrals of non-convolution type
T is said to be a singular integral operator of non-convolution type associated to the Calderón–Zygmund kernel K if
whenever f and g are smooth and have disjoint support. Such operators need not be bounded on Lp
Calderón–Zygmund operators
A singular integral of non-convolution type T associated to a Calderón–Zygmund kernel K is called a Calderón–Zygmund operator when it is bounded on L2, that is, there is a C > 0 such that
for all smooth compactly supported ƒ.
It can be proved that such operators are, in fact, also bounded on all Lp with 1 < p < ∞.
The T(b) theorem
The T(b) theorem provides sufficient conditions for a singular integral operator to be a Calderón–Zygmund operator, that is for a singular integral operator associated to a Calderón–Zygmund kernel to be bounded on L2. In order to state the result we must first define some terms.A normalised bump is a smooth function φ on Rn supported in a ball of radius 10 and centred at the origin such that |∂α φ(x)| ≤ 1, for all multi-indices |α| ≤ n + 2. Denote by τx(φ)(y) = φ(y − x) and φr(x) = r−nφ(x/r) for all x in Rn and r > 0. An operator is said to be weakly bounded if there is a constant C such that
for all normalised bumps φ and ψ. A function is said to be accretive if there is a constant c > 0 such that Re(b)(x) ≥ c for all x in R. Denote by Mb the operator given by multiplication by a function b.
The T(b) theorem states that a singular integral operator T associated to a Calderón–Zygmund kernel is bounded on L2 if it satisfies all of the following three conditions for some bounded accretive functions b1 and b2:
(a)
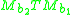is weakly bounded;(b)
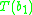is in BMOBounded mean oscillation
In harmonic analysis, a function of bounded mean oscillation, also known as a BMO function, is a real-valued function whose mean oscillation is bounded...
;
(c)
is in BMOBounded mean oscillation
In harmonic analysis, a function of bounded mean oscillation, also known as a BMO function, is a real-valued function whose mean oscillation is bounded...
, where Tt is the transpose operator of T.