
Cartesian product of graphs
Encyclopedia
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the Cartesian product G
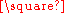 H of graphs G and H is a graph such that
H of graphs G and H is a graph such that
- the vertex set of G
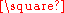 H is the Cartesian productCartesian productIn mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
H is the Cartesian productCartesian productIn mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
V(G) × V(H); and - any two vertices (u,u') and (v,v') are adjacent in G
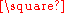 H if and only if either
H if and only if either
- u = v and u' is adjacent with v' in H, or
- u' = v' and u is adjacent with v in G.
Cartesian product graphs can be recognized efficiently, in time O(m log n) for a graph with m edges and n vertices . The operation is commutative as an operation on isomorphism
Graph isomorphism
In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...
classes of graphs, and more strongly the graphs G
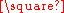 H and H
H and H 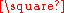 G are naturally isomorphic, but it is not commutative as an operation on labeled graphs. The operation is also associative, as the graphs (F
G are naturally isomorphic, but it is not commutative as an operation on labeled graphs. The operation is also associative, as the graphs (F 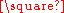 G)
G) 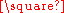 H and F
H and F 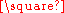 (G
(G 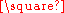 H) are naturally isomorphic.
H) are naturally isomorphic.The notation G × H is occasionally also used for Cartesian products of graphs, but is more commonly used for another construction known as the tensor product of graphs
Tensor product of graphs
In graph theory, the tensor product G × H of graphs G and H is a graph such that* the vertex set of G × H is the Cartesian product V × V; and...
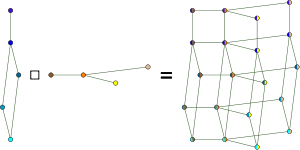
. The square symbol is the more common and unambiguous notation for the Cartesian product of graphs. It shows visually the four edges resulting from the Cartesian product of two edges.
The Cartesian product is not a product
Product (category theory)
In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
in the category of graphs. (The tensor product is the categorical product.) The category of graphs do form a monoidal category
Monoidal category
In mathematics, a monoidal category is a category C equipped with a bifunctorwhich is associative, up to a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism...
under the Cartesian product.
Examples
- The Cartesian product of two edges is a cycleCycle graphIn graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...
on four vertices: K2 K2 = C4.
K2 = C4. - The Cartesian product of K2 and a path graphPath graphIn the mathematical field of graph theory, a path graph or linear graph is a particularly simple example of a tree, namely a tree with two or more vertices that is not branched at all, that is, contains only vertices of degree 2 and 1...
is a ladder graphLadder graphIn the mathematical field of graph theory, the ladder graph Ln is a planar undirected graph with 2n vertices and n+2 edges....
. - The Cartesian product of two path graphs is a grid graph.
- The Cartesian product of n edges is a hypercube:
-
-
- Thus, the Cartesian product of two hypercube graphs is another hypercube: Qi
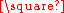 Qj = Qi+j.
Qj = Qi+j.
- The Cartesian product of two median graphMedian graphIn mathematics, and more specifically graph theory, a median graph is an undirected graph in which any three vertices a, b, and c have a unique median: a vertex m that belongs to shortest paths between any two of a, b, and c.The concept of median graphs has long been studied, for instance by or ...
s is another median graph. - The graph of vertices and edges of an n-prismPrism (geometry)In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
is the Cartesian product graph K2 Cn.
Cn. - The rook's graphRook's graphIn graph theory, a rook's graph is a graph that represents all legal moves of the rook chess piece on a chessboard: each vertex represents a square on a chessboard and each edge represents a legal move...
is the Cartesian product of two complete graphs.
- The Cartesian product of two median graph
Properties
If a connected graph is a Cartesian product, it can be factorized uniquely as a product of prime factors, graphs that cannot themselves be decomposed as products of graphs (Sabidussi 1960; Vizing 1963). However, Imrich and Klavžar (2000) describe a disconnected graph that can be expressed in two different ways as a Cartesian product of prime graphs: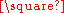 (K1 + K23) = (K1 + K22 + K24)
(K1 + K23) = (K1 + K22 + K24) 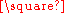 (K1 + K2),
(K1 + K2),where the plus sign denotes disjoint union and the superscripts denote exponentiation over Cartesian products.
A Cartesian product is vertex transitive
Vertex-transitive graph
In the mathematical field of graph theory, a vertex-transitive graph is a graph G such that, given any two vertices v1 and v2 of G, there is some automorphismf:V \rightarrow V\ such thatf = v_2.\...
if and only if each of its factors is (Imrich and Klavžar, Theorem 4.19).
A Cartesian product is bipartite
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
if and only if each of its factors is. More generally, the chromatic number of the Cartesian product satisfies the equation
- χ(G
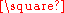 H) = max {χ(G), χ(H)}
H) = max {χ(G), χ(H)}
(Sabidussi 1957). The Hedetniemi conjecture states a related equality for the tensor product of graphs
Tensor product of graphs
In graph theory, the tensor product G × H of graphs G and H is a graph such that* the vertex set of G × H is the Cartesian product V × V; and...
. The independence number of a Cartesian product is not so easily calculated, but as Vizing (1963) showed it satisfies the inequalities
- α(G)α(H) + min{|V(G)|-α(G),|V(H)|-α(H)} ≤ α(G
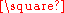 H) ≤ min{α(G) |V(H)|, α(H) |V(G)|}.
H) ≤ min{α(G) |V(H)|, α(H) |V(G)|}.
The Vizing conjecture states that the domination number of a Cartesian product satisfies the inequality
- γ(G
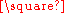 H) ≥ γ(G)γ(H).
H) ≥ γ(G)γ(H).
History
According to Klavžar and Imrich, Cartesian products of graphs were defined in 1912 by WhiteheadAlfred North Whitehead
Alfred North Whitehead, OM FRS was an English mathematician who became a philosopher. He wrote on algebra, logic, foundations of mathematics, philosophy of science, physics, metaphysics, and education...
and Russell
Bertrand Russell
Bertrand Arthur William Russell, 3rd Earl Russell, OM, FRS was a British philosopher, logician, mathematician, historian, and social critic. At various points in his life he considered himself a liberal, a socialist, and a pacifist, but he also admitted that he had never been any of these things...
. They were repeatedly rediscovered later, notably by Sabidussi in 1960.


