
Cap product
Encyclopedia
In algebraic topology
the cap product is a method of adjoining a chain
of degree p with a cochain of degree q, such that q ≤ p, to form a composite chain of degree p − q. It was introduced by Eduard Čech
in 1936, and independently by Hassler Whitney
in 1938.
and R a coefficient ring. The cap product is a bilinear map on singular homology and cohomology
defined by contracting a singular chain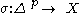 with a singular cochain
with a singular cochain 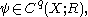 by the formula :
by the formula :

Here, the notation indicates the restriction of the simplicial map
indicates the restriction of the simplicial map  to its face spanned by the vectors of the base, see Simplex
to its face spanned by the vectors of the base, see Simplex
.
in terms of the Kunneth formula, we can explain the existence of the cap product by considering the composition
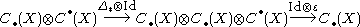
in terms of the chain
and cochain complexes of , where we are taking tensor products of chain complexes
, where we are taking tensor products of chain complexes
,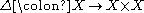 is the diagonal map which induces the map
is the diagonal map which induces the map 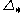 on the chain complex (more precisely, the map
on the chain complex (more precisely, the map 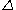 is not cellular
is not cellular
, but as detailed in that article, any continuous map of CW complex
es is homotopic
to a cellular map, so we are in effect considering an associated cellular map to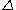 , the choice of homotopic map does not end up mattering when we pass to the quotient), and
, the choice of homotopic map does not end up mattering when we pass to the quotient), and 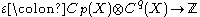 is the evaluation map (always 0 except for
is the evaluation map (always 0 except for 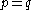 ).
).
This composition then passes to the quotient to define the cap product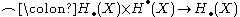 , and looking carefully at the above composition shows that it indeed takes the form of maps
, and looking carefully at the above composition shows that it indeed takes the form of maps 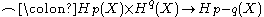 , which is always zero for
, which is always zero for 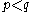 .
.
s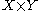 yielding a product
yielding a product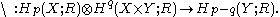
In case X = Y, the two products are related by the diagonal map.
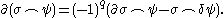
Given a map f the induced maps satisfy :
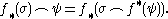
The cap and cup product
are related by :
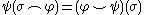
where
 ,
, 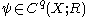 and
and 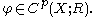
An interesting consequence of the last equation is that it makes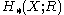 into a right
into a right  module
module
.
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
the cap product is a method of adjoining a chain
Chain (algebraic topology)
In algebraic topology, a simplicial k-chainis a formal linear combination of k-simplices.-Integration on chains:Integration is defined on chains by taking the linear combination of integrals over the simplices in the chain with coefficients typically integers.The set of all k-chains forms a group...
of degree p with a cochain of degree q, such that q ≤ p, to form a composite chain of degree p − q. It was introduced by Eduard Čech
Eduard Cech
Eduard Čech was a Czech mathematician born in Stračov, Bohemia . His research interests included projective differential geometry and topology. In 1921–1922 he collaborated with Guido Fubini in Turin...
in 1936, and independently by Hassler Whitney
Hassler Whitney
Hassler Whitney was an American mathematician. He was one of the founders of singularity theory, and did foundational work in manifolds, embeddings, immersions, and characteristic classes.-Work:...
in 1938.
Definition
Let X be a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
and R a coefficient ring. The cap product is a bilinear map on singular homology and cohomology

defined by contracting a singular chain
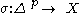 with a singular cochain
with a singular cochain 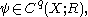 by the formula :
by the formula :
Here, the notation
 indicates the restriction of the simplicial map
indicates the restriction of the simplicial map  to its face spanned by the vectors of the base, see Simplex
to its face spanned by the vectors of the base, see SimplexSimplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
.
Interpretation
In analogy with the interpretation of the cup productCup product
In mathematics, specifically in algebraic topology, the cup product is a method of adjoining two cocycles of degree p and q to form a composite cocycle of degree p + q. This defines an associative graded commutative product operation in cohomology, turning the cohomology of a space X into a...
in terms of the Kunneth formula, we can explain the existence of the cap product by considering the composition
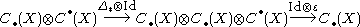
in terms of the chain
Chain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
and cochain complexes of
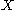 , where we are taking tensor products of chain complexes
, where we are taking tensor products of chain complexesKünneth theorem
In mathematics, especially in homological algebra and algebraic topology, a Künneth theorem is a statement relating the homology of two objects to the homology of their product. The classical statement of the Künneth theorem relates the singular homology of two topological spaces X and Y and their...
,
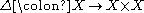 is the diagonal map which induces the map
is the diagonal map which induces the map 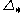 on the chain complex (more precisely, the map
on the chain complex (more precisely, the map 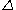 is not cellular
is not cellularCellular approximation
In algebraic topology, in the cellular approximation theorem, a map between CW-complexes can always be taken to be of a specific type. Concretely, if X and Y are CW-complexes, and f : X → Y is a continuous map, then f is said to be cellular, if f takes the n-skeleton of X to the n-skeleton of Y for...
, but as detailed in that article, any continuous map of CW complex
CW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
es is homotopic
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
to a cellular map, so we are in effect considering an associated cellular map to
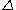 , the choice of homotopic map does not end up mattering when we pass to the quotient), and
, the choice of homotopic map does not end up mattering when we pass to the quotient), and 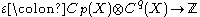 is the evaluation map (always 0 except for
is the evaluation map (always 0 except for 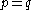 ).
).This composition then passes to the quotient to define the cap product
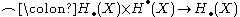 , and looking carefully at the above composition shows that it indeed takes the form of maps
, and looking carefully at the above composition shows that it indeed takes the form of maps 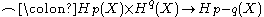 , which is always zero for
, which is always zero for 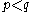 .
.The slant product
The above discussion indicates that the same operation can be defined on cartesian productCartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
s
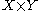 yielding a product
yielding a product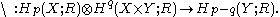
In case X = Y, the two products are related by the diagonal map.
Equations
The boundary of a cap product is given by :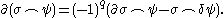
Given a map f the induced maps satisfy :
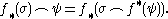
The cap and cup product
Cup product
In mathematics, specifically in algebraic topology, the cup product is a method of adjoining two cocycles of degree p and q to form a composite cocycle of degree p + q. This defines an associative graded commutative product operation in cohomology, turning the cohomology of a space X into a...
are related by :
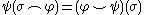
where
 ,
, 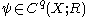 and
and 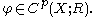
An interesting consequence of the last equation is that it makes
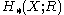 into a right
into a right  module
moduleModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
.

