Cellular approximation
Encyclopedia
In algebraic topology
, in the cellular approximation theorem, a map
between CW-complexes can always be taken to be of a specific type. Concretely, if X and Y are CW-complexes, and f : X → Y is a continuous map, then f is said to be cellular, if f takes the n-skeleton
of X to the n-skeleton of Y for all n, i.e. if
for all n. The content of the cellular approximation theorem is then that any continuous map f : X → Y between CW-complexes X and Y is homotopic
to a cellular map, and if f is already cellular on a subcomplex A of X, then we can furthermore choose the homotopy to be stationary on A. From an algebraic topological viewpoint, any map between CW-complexes can thus be taken to be cellular.
after n, with the statement that f is cellular on the skeleton Xn. For the base case n=0, notice that every path-component of Y must contain a 0-cell. The image
under f of a 0-cell of X can thus be connected to a 0-cell of Y by a path, but this gives a homotopy from f to a map, which is cellular on the 0-skeleton of X.
Assume inductively that f is cellular on the (n − 1)-skeleton of X, and let en be an n-cell of X. The closure
of en is compact in X, being the image of the characteristic map of the cell, and hence the image of the closure of en under f is also compact in Y. Then it is a general result of CW-complexes that any compact subspace of a CW-complex meets (that is, intersects
non-trivially) only finitely many cells of the complex. Thus f(en) meets at most finitely many cells of Y, so we can take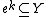
to be a cell of highest dimension meeting f(en). If 
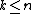, the map f is already cellular on en, since in this case only cells of the n-skeleton of Y meets f(en), so we may assume that k > n. It is then a technical, non-trivial result (see Hatcher) that the restriction of f to 
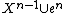can be homotoped relative to Xn-1 to a map missing a point p ∈ ek. Since Yk − {p} deformation retracts onto the subspace Yk-ek, we can further homotope the restriction of f to 
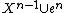to a map, say, g, with the property that g(en) misses the cell ek of Y, still relative to Xn-1. Since f(en) met only finitely many cells of Y to begin with, we can repeat this process finitely many times to make 
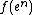miss all cells of Y of dimension larger than n.
We repeat this process for every n-cell of X, fixing cells of the subcomplex A on which f is already cellular, and we thus obtain a homotopy (relative to the (n − 1)-skeleton of X and the n-cells of A) of the restriction of f to Xn to a map cellular on all cells of X of dimension at most n. Using then the homotopy extension property
to extend this to a homotopy on all of X, and patching these homotopies together, will finish the proof. For details, consult Hatcher.
. In particular, if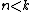
, then 
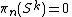: Give 
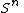and 
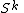their canonical CW-structure, with one 0-cell each, and with one n-cell for 
and one k-cell for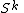 
. Any base-point preserving map f:
→
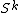is by the cellular approximation theorem homotopic to a constant map, whence 
.
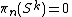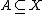under f sits inside B. Then f is homotopic to a cellular map (X,A)→(Y,B). To see this, restrict f to A and use cellular approximation to obtain a homotopy of f to a cellular map on A. Use the homotopy extension property to extend this homotopy to all of X, and apply cellular approximation again to obtain a map cellular on X, but without violating the cellular property on A.
As a consequence, we have that a CW-pair (X,A) is n-connected
, if all cells of
have dimension strictly greater than n: If 
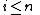, then any map 
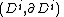→(X,A) is homotopic to a cellular map of pairs, and since the n-skeleton of X sits inside A, any such map is homotopic to a map whose image is in A, and hence it is 0 in the relative homotopy group 
.
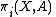We have in particular that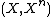
is n-connected, so it follows from the long exact sequence of homotopy groups for the pair 
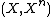that we have isomorphisms 
→
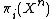for all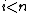 
and a surjection 
→
.
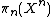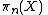Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, in the cellular approximation theorem, a map
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
between CW-complexes can always be taken to be of a specific type. Concretely, if X and Y are CW-complexes, and f : X → Y is a continuous map, then f is said to be cellular, if f takes the n-skeleton
N-skeleton
In mathematics, particularly in algebraic topology, the n-skeleton of a topological space X presented as a simplicial complex refers to the subspace Xn that is the union of the simplices of X of dimensions m ≤ n...
of X to the n-skeleton of Y for all n, i.e. if
for all n. The content of the cellular approximation theorem is then that any continuous map f : X → Y between CW-complexes X and Y is homotopicHomotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
to a cellular map, and if f is already cellular on a subcomplex A of X, then we can furthermore choose the homotopy to be stationary on A. From an algebraic topological viewpoint, any map between CW-complexes can thus be taken to be cellular.
Idea of proof
The proof can be given by inductionMathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
after n, with the statement that f is cellular on the skeleton Xn. For the base case n=0, notice that every path-component of Y must contain a 0-cell. The image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
under f of a 0-cell of X can thus be connected to a 0-cell of Y by a path, but this gives a homotopy from f to a map, which is cellular on the 0-skeleton of X.
Assume inductively that f is cellular on the (n − 1)-skeleton of X, and let en be an n-cell of X. The closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of en is compact in X, being the image of the characteristic map of the cell, and hence the image of the closure of en under f is also compact in Y. Then it is a general result of CW-complexes that any compact subspace of a CW-complex meets (that is, intersects
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
non-trivially) only finitely many cells of the complex. Thus f(en) meets at most finitely many cells of Y, so we can take
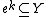to be a cell of highest dimension meeting f(en). If 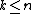, the map f is already cellular on en, since in this case only cells of the n-skeleton of Y meets f(en), so we may assume that k > n. It is then a technical, non-trivial result (see Hatcher) that the restriction of f to 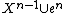can be homotoped relative to Xn-1 to a map missing a point p ∈ ek. Since Yk − {p} deformation retracts onto the subspace Yk-ek, we can further homotope the restriction of f to 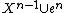to a map, say, g, with the property that g(en) misses the cell ek of Y, still relative to Xn-1. Since f(en) met only finitely many cells of Y to begin with, we can repeat this process finitely many times to make 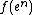miss all cells of Y of dimension larger than n.We repeat this process for every n-cell of X, fixing cells of the subcomplex A on which f is already cellular, and we thus obtain a homotopy (relative to the (n − 1)-skeleton of X and the n-cells of A) of the restriction of f to Xn to a map cellular on all cells of X of dimension at most n. Using then the homotopy extension property
Homotopy extension property
In mathematics, in the area of algebraic topology, the homotopy extension property indicates when a homotopy defined on a subspace can be extended to a homotopy defined on a larger space.-Definition:Let X\,\! be a topological space, and let A \subset X....
to extend this to a homotopy on all of X, and patching these homotopies together, will finish the proof. For details, consult Hatcher.
Some homotopy groups
The cellular approximation theorem can be used to immediately calculate some homotopy groupsHomotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
. In particular, if
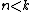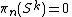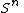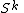, then : Give and their canonical CW-structure, with one 0-cell each, and with one n-cell for and one k-cell for 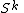. Any base-point preserving map f:→ 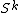is by the cellular approximation theorem homotopic to a constant map, whence 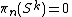.Cellular approximation for pairs
Let f:(X,A)→(Y,B) be a map of CW-pairs, that is, f is a map from X to Y, and the image of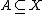 under f sits inside B. Then f is homotopic to a cellular map (X,A)→(Y,B). To see this, restrict f to A and use cellular approximation to obtain a homotopy of f to a cellular map on A. Use the homotopy extension property to extend this homotopy to all of X, and apply cellular approximation again to obtain a map cellular on X, but without violating the cellular property on A.As a consequence, we have that a CW-pair (X,A) is n-connected
N-connected
In the mathematical branch of algebraic topology, specifically homotopy theory, n-connectedness is a way to say that a space vanishes or that a map is an isomorphism "up to dimension n, in homotopy".-n-connected space:...
, if all cells of
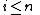have dimension strictly greater than n: If , then any map 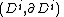→(X,A) is homotopic to a cellular map of pairs, and since the n-skeleton of X sits inside A, any such map is homotopic to a map whose image is in A, and hence it is 0 in the relative homotopy group 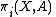.We have in particular that
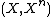is n-connected, so it follows from the long exact sequence of homotopy groups for the pair 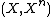that we have isomorphisms 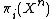→ for all 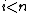and a surjection →.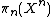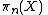